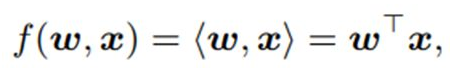CVPR2018 | Decoupled Networks
加入极市专业CV交流群,与6000+来自腾讯,华为,百度,北大,清华,中科院等名企名校视觉开发者互动交流!更有机会与李开复老师等大牛群内互动!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。点击文末“阅读原文”立刻申请入群~
ps.CVPR2019 accepted list已经公布,极市已将目前收集到的公开论文总结到github上(目前已收集243篇),后续会不断更新,欢迎关注,也欢迎大家提交自己的论文:
https://github.com/extreme-assistant/cvpr2019
最近分享了很多CVPR2019的论文解读,今日回顾一篇CVPR2018论文:Decoupled Networks
作者 | iker peng
来源 | https://zhuanlan.zhihu.com/p/37598903
论文地址 | https://arxiv.org/pdf/1804.08071.pdf
一篇优秀的论文,就是你看到就忍不住要分享下,这篇CVPR2018的论文就是这样的一篇。为什么这是一篇好的论文呢?因为它有一个好的问题,并且给出了一个靠谱的解决方案,甚至更加具有一般性。大量的实验验证了自己在实践上也是非常有效的。甚至故事讲得也非常的棒,并且算法思路清晰惊艳。
如果我问你神经网络(这里重点放在CNN上,对于其余的网络模型也具有一般性)机制上存在哪些缺陷,并且相应的产出了哪些解决方案?你能够想到多少呢?
过拟合,梯度消失或者是膨胀,训练依靠大量的样本,对网络初始化极其敏感以及协迁移等等。相信针对这些问题所提出的网络的改进方案大家也不陌生,很多的模块已经成为现在DL的标配了。
那么对于操作子(Operator)本身的改进的工作多不多呢? 显然对于这种重新造轮子的事情大家还是不太有勇气去尝试的。而这篇文章的工作就是在重新定义操作子,自己造轮子。
要打操作子的主意,那么首先得说说现在的卷积操作子有什么问题吧。卷积操作其实就是一个内积的操作:
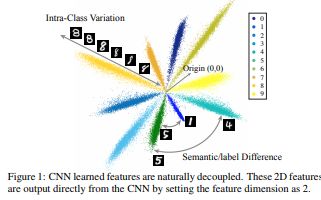
其本质上是一个:矩阵相乘计算 两个矩阵相似度的操作(类似卷积滤波)。而本文的核心就是为了解耦(Decouple)这个操作。那么这种操作到底是什么内容的耦合呢? 简单来讲,类内差异(intra-class variation)和类间差异(inter-class difference)的耦合。也就是说当你通过卷积操作得到的结果很相似的时候,你并不能够得到一个结论说这两个很相似,反之亦不能。 因为你不能够区别这种差异或者是相似度是类内差异造成的还是类间的差异造成的(而对于分类的问题来讲,我们其实关心的就是 类间差异而已)。说起来有点抽象,我们具体来看一下这张图:
这张图是 CNN在手写体识别任务上学到的特征的2D可视化示意图。 0~9每一个手写体数字对应的特征是图中的一束;任意一束当中的不同位置表示的是同一类别的不同表征,也就是类间差距(intra-class Variations);束与束之间形成的夹角表达的是两个类别之间的差距(inter-class difference),也就是这里所谓的语义差异。
如果不解耦会存在一个什么样的问题呢?就是说你只能得到一个最终的结果,但是对于两个同样的输出,你不能分辨造成这个结果的原因是因为他们实际就是同一种类别,还是因为刚好 ab =cd。那么具体怎么解耦呢? 作者给出的解决方案真是精简:
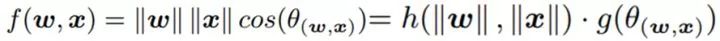
,直接将卷积操作解耦表示为 幅值 (Norm)和 角度(Angle)两个部分,并且将这两部分分别用两个函数h(.) 和g(.)来表示,毫无疑问其中的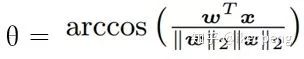
因此关于角度的函数g(.)则度量着不同的类别之间的差异(inter-class difference),关于幅值的函数h(.)则度量着同一类别当中的差异(intra-class variations),同时其值的大小也就表示了这个类别的可信度。这种思路是不是非常的精妙啊!同时,传统的卷积操作就变成了解耦网络的一个特例,即:
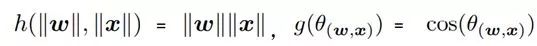
为什么角度可以来衡量类别之间的差异呢?作者是从傅里叶变换当中的得到的motivation: 对于傅里叶变换来说,两个概念非常的重要,一个就是幅值,另一个就是相位。对于一张图像的傅里叶变换,如果你使用幅值和随机的相位重建这张图像,得到的结果往往不能辨认;但是如果你使用相位和随机的幅值却能够重建出能够辨认的图像。
到此为止,文章最核心的部分已经讲完。接下来作者讨论了各种关于这两个函数的设计,包括有界的,无界的;加权的不加权的以及解耦网络的几何解释等等。那么具体文章设计出来的h(.) 和g(.)函数表示为以下:
需要注意的是这里讨论的都是不加权的解耦操作子,也就是说所有的权重被认为是同等的重要:h(||ω||, ||x||)= h(||x||). 同时作者在实验当中说明了,其实这样的操作简化了操作同时也保证了准度。
对于h(||ω||, ||x||),举几个重要的例子来说:
1 . SphereCov: 即 h(||ω||, ||x||) =α, 也就是说对于任何一个类别,其实我并不关心他们的类内差异,我只想要得到一个最终的类间差异,因此,我将这个最终决定权全部交给g(.)。所以你会发现所有的类别的特征都会投影在一个球面(Sphere)上面。
2 . BallCov: 从名字来讲我们就知道,特征的投影会是一个实心的球(Ball),也就是说我考虑类内的差异,但是这个差异有一个上界那就是这个球的球面,而在球的内部,其重要性是和输入相关的。即:
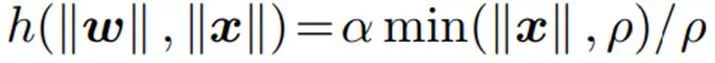
其中的 ρ就是Ball的半径。
3 . TanhConv:也很简单,就不过多的解释了:
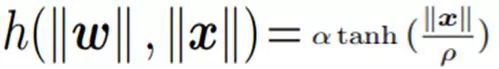
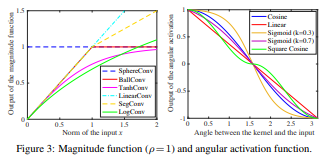
通过这三种操作子得到的特征的可视化可以表示为:
注意 SphereCov更多是投影在球面的,而后面的两个理论上可以看做是一个实心的。
那么我们再来看一下g(.), g(.) 是一个关于θ的函数,大多数实际上是一个非线性的函数,也就是说其实就是一个激活函数,这里作者称之为角度激活函数(Angular activation)。 那么理论上来讲,这样的操作子是不需要再有一个激活函数的。作者列出了几种g(.) 的选择,最简单的就是这两个,也很好理解:
Linear:
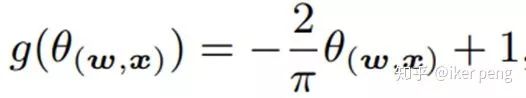
Cosine:
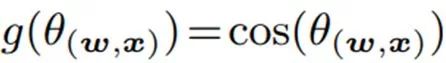
具体的细节请参考原文,那么我们来看一下大家最关心的结果。
实验的部分,作者做了大量的实验,不仅比较了设计的DN网络的收敛性,非线性,BN功能,而且还和ResNet等比较下目标识别任务上的准确度,此外作者还对网络对于对抗样本攻击的性能进行了比较。在所有的比较当中作者都得到了最好的结果。主要看以下几个方面的比较:
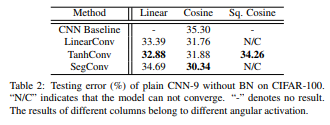
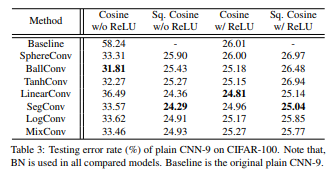
1.在CIFAR100上和没有BN的CNN:
注意,这个表格当中,每一行都是一个 卷积操作子也就是 h(.)Norm函数,每一列都是一个 角度激活函数g(.)。因此,如之前所说,对于一个一般CNN 就是g(.)=Cosine。
结果显示,即便是没有BN,DN都能够表现出绝对的优势。
2. 操作子的非线性的比较
第一列的比较非常明显的看出,在没有ReLU激活函数的情况下,一般的CNN可以达到高达58%以上的错误率,而对于DN来讲只有差不多30%;而从第三列再加上ReLU之后,DN的性能也好于传统的CNN。
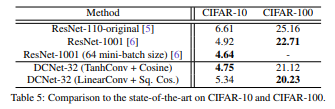
3. 目标识别性能比较:
作者是 CIFAR10 和CIFAR100 两个数据集上面和当前最好的网络模型进行了分类准确度的比较,我们可以看出。DN都可以拿到最好的结果。同时作者也在ImageNet-2012上进行了比较,也同样拿到了最好的效果:
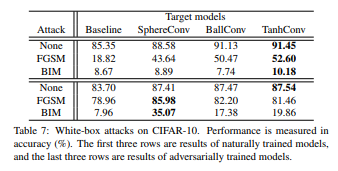
4. 对抗样本攻击的比较
作者在黑盒和白盒的情况下,比较了两种算法的攻击:FGSM和BIM。结果显示其具有更好的防止攻击的能力。
非常推荐这篇文章!
*延伸阅读
点击左下角“阅读原文”,即可申请加入极市目标跟踪、目标检测、工业检测、人脸方向、视觉竞赛等技术交流群,更有每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流,一起来让思想之光照的更远吧~
觉得有用麻烦给个好看啦~