小孩都看得懂的主成分分析

全文共  2210  字， 19  幅图，

预计阅读时间  12  分钟。

本文是「小孩都看得懂」系列的第五篇，本系列的特点是极少公式，没有代码，只有图画，只有故事。内容不长，碎片时间完全可以看完，但我背后付出的心血却不少。喜欢就好！

1. 小孩都看得懂的神经网络

2. 小孩都看得懂的推荐系统

3. 小孩都看得懂的逐步提升

4. 小孩都看得懂的聚类

5. 小孩都看得懂的主成分分析

本文所有思路都来自 Luis Serrano 的油管视屏「Principle Component Analysis (PCA)」，纯纯的致敬！

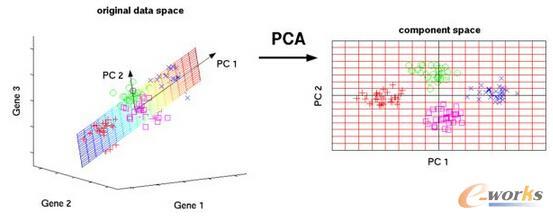
PCA 是无监督学习中的最常见的数据降维方法，但实际问题特征很多的情况，PCA 通常会预处理来减少特征个数。

1

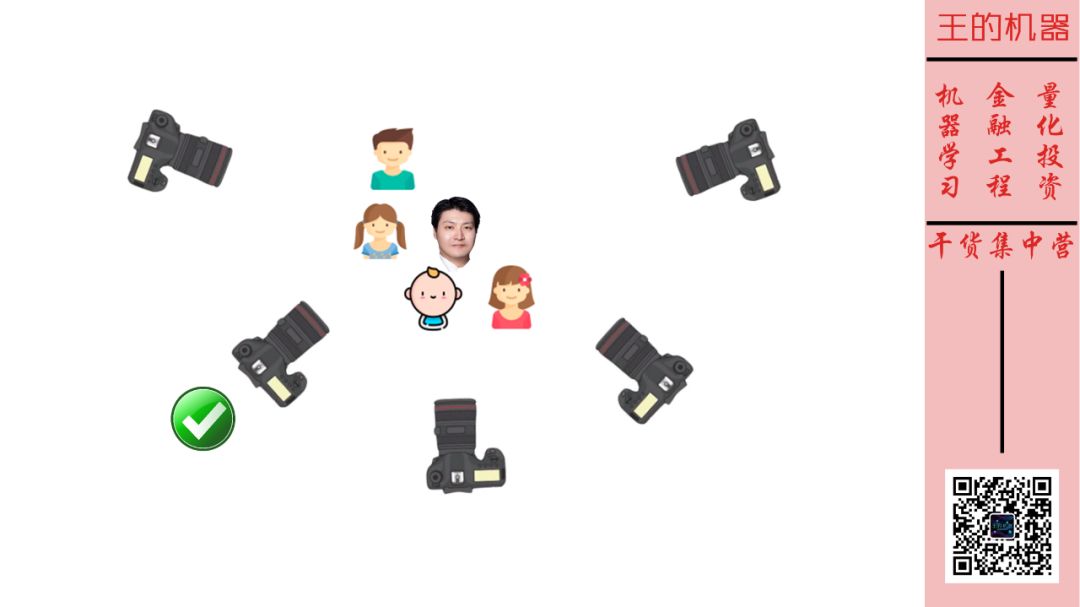
提问：如果给我们 5 个人照相，照相机应该放在哪？

回答：放在图中打钩的地方，因为人脸面对照相机正面分布最开，最容易把所有人脸都照进来。

思考：人脸分布最开 ≈ 数据方差最大？

2

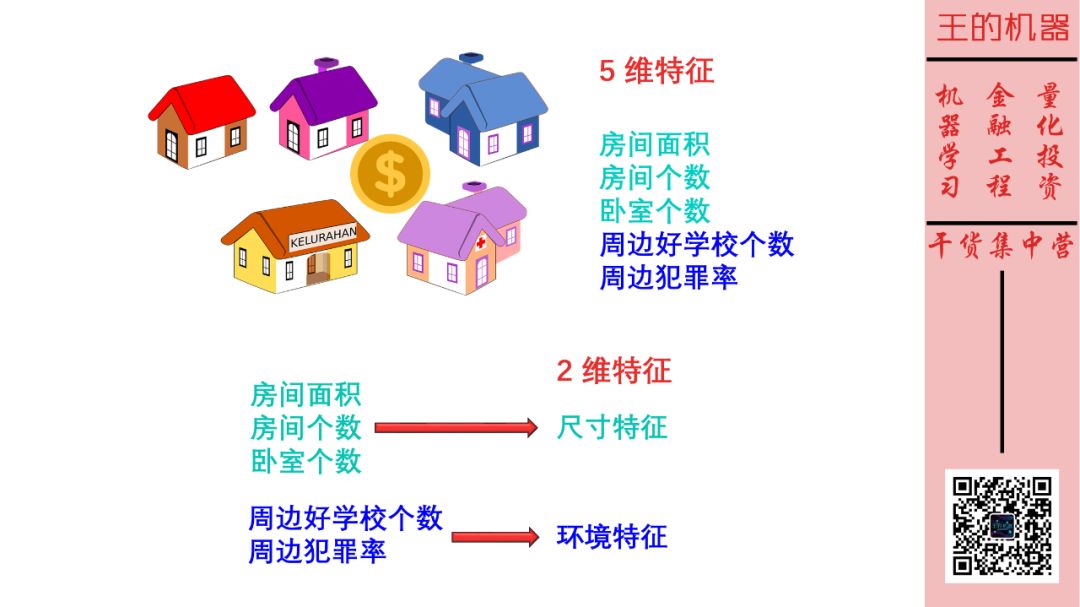
试想预测房价的场景，假如我们用 5 个特征来预测房价，它们是

1. 房间面积
   

2. 房间个数

3. 卧室个数

4. 周边好学校个数

5. 周边犯罪率

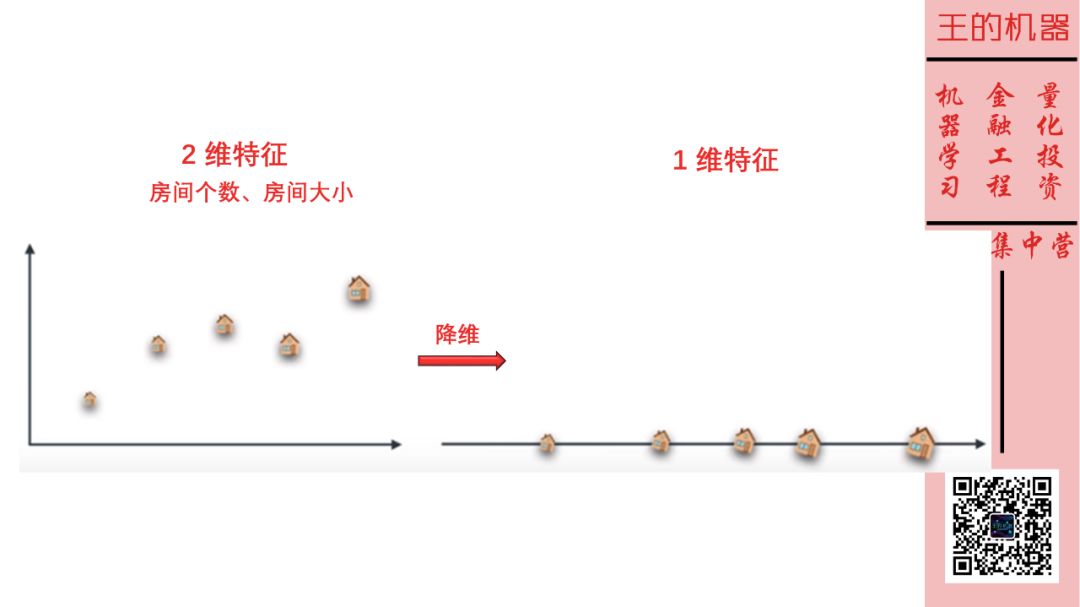
但仔细一看，这 5 个特征可以抽象成 2 个，前三个都在讨论「尺寸」而后两个都在讨论「环境」。那么是否可以把这 5 维特征降到 2 维特征呢？

3

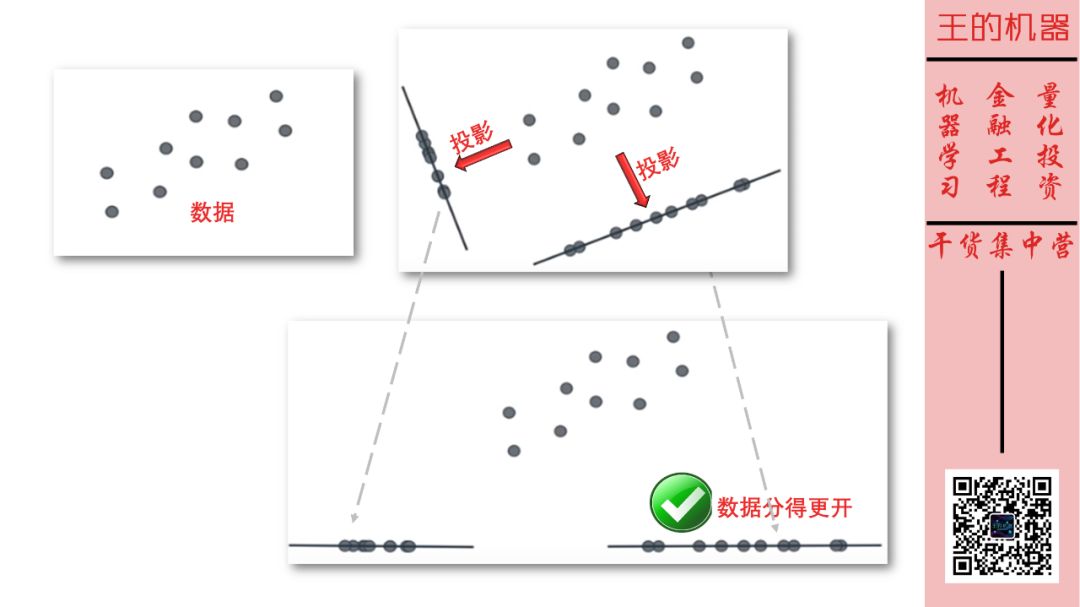
5 维数据太难可视化，人还是最容易可视化 2 维数据。

给定 2 维数据，如果向两条线上做投影，应该选择投影后数据分得更开的那条线。试想假如接下来做分类是不是更容易些？

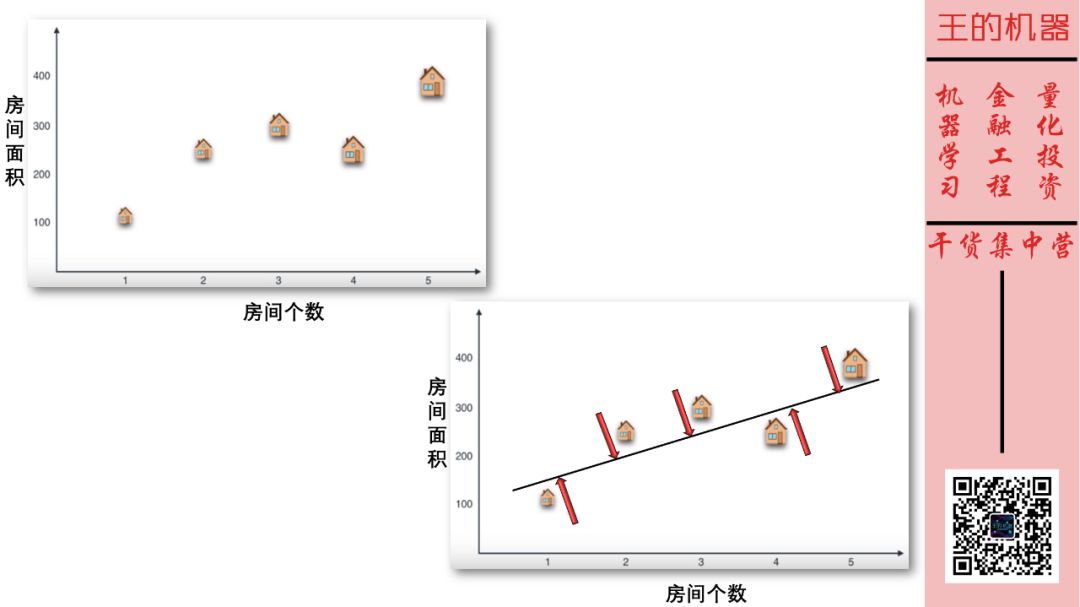
将这 2 维特征实例化为房间面积和房间个数，它们通常成正比关系。假设我们找到一条向上的直线，将这 2 维特征投影到该直线上，如下图。

特征房间面积和房间个数有些重复了，因此把它们降到 1 维也没有丢失太多信息，如下图。

4

场景有了，直觉也有了，那么我们该看看 PCA 背后的数学原理了。其实非常简单，你只用知道均值、方差、协方差这三个基本统计概念就行了。原谅我这次必须要带点公式，但我相信现在小孩应该能懂。

均值

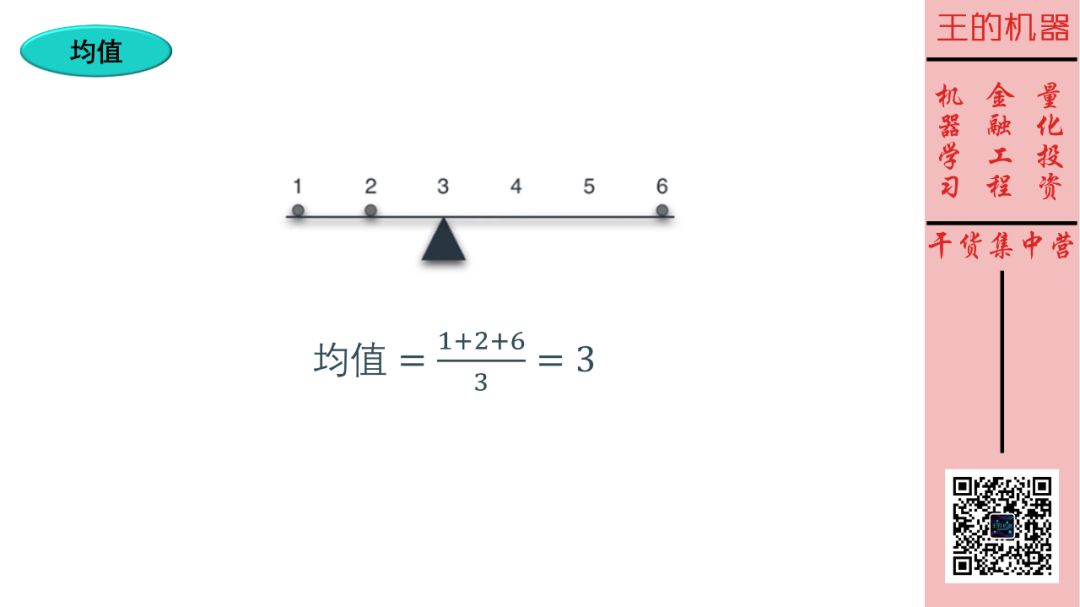
均值不要太简单，自己看图，我不解释了行吗？

方差

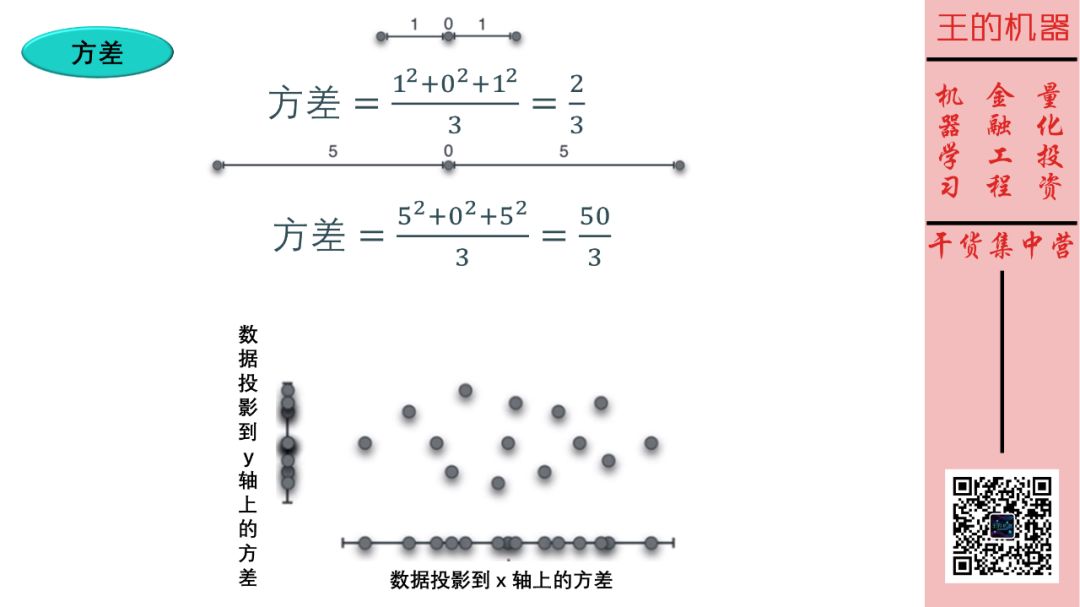
方差的概念稍微难些。方差是衡量数据和其均值的偏离程度。如上图上半部分，两组数据的均值都为 0 ，而第二组数据的方差 (50/3) 大于第一组数据的方差 (2/3)，因此第二组数据更加分散些。 

同理，看上图下半部分，数据投影到 x 轴上的方差大于数据投影到 y 轴上的方差。

最后给出计算 N 个数据的方差极简公式 (将每个数据的值减去其均值，平方后再求平均)

    X 方差 = 加总(Xi - 均值)2 / N

    Y 方差 = 加总(Yi - 均值)2 / N

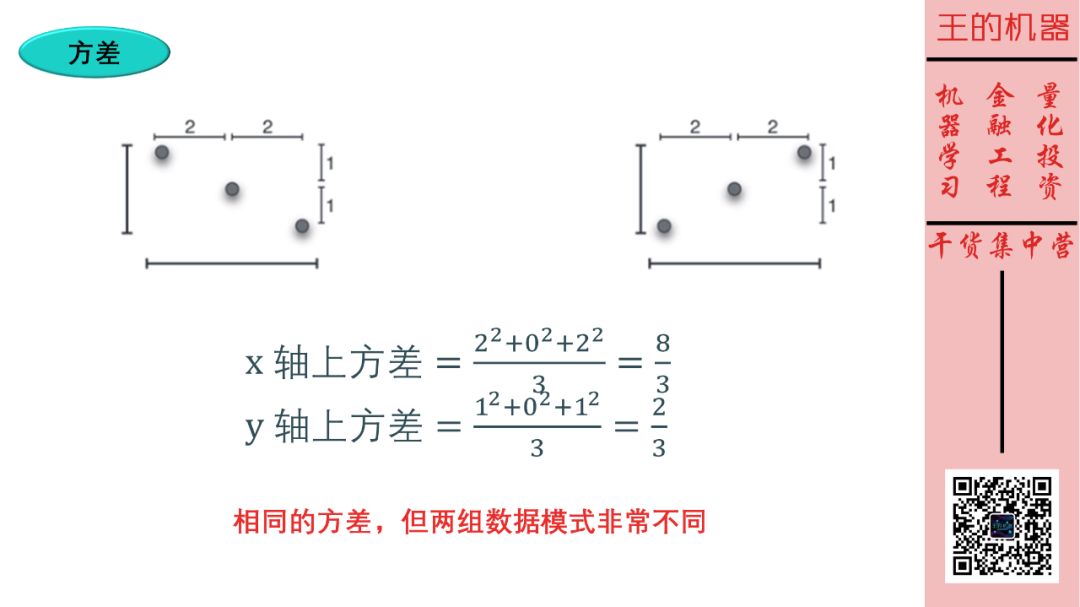
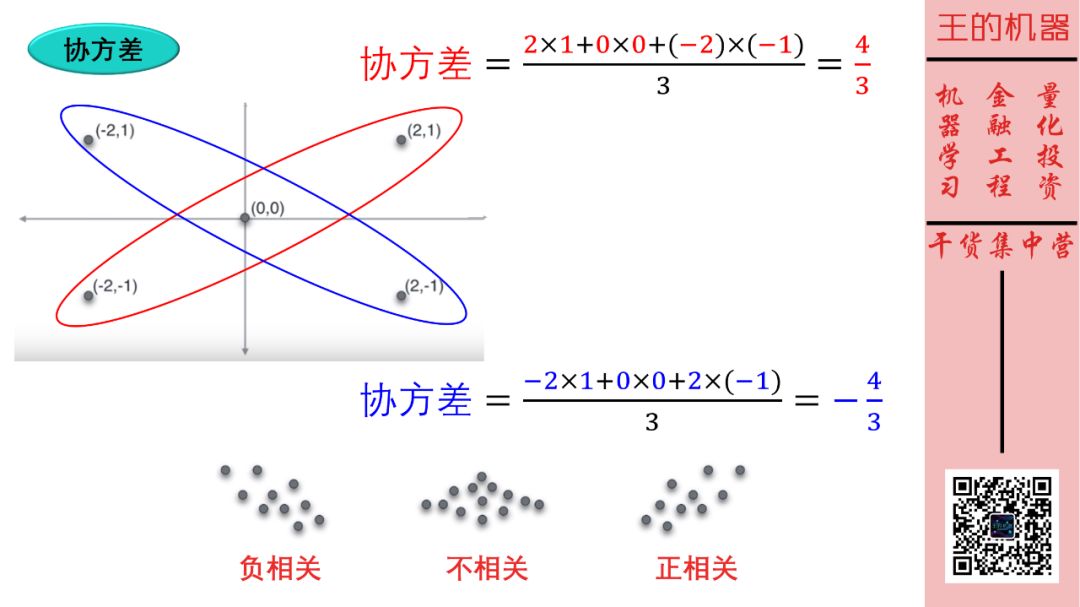
接着来看两组数据，它们具有相同的方差 (投影到 x 轴和 y 轴)，但是这两组数据的模式非常不同，一个趋势向下，一个趋势向上。

这样看来，光靠方差是不能准确描述不同的数据模式了，是时候该介绍协方差了。

协方差

首先给出计算 N 个数据的协方差极简公式 (将数据 X 值和 Y 值相乘，再求平均)

    协方差 = 加总(Xi × Yi) / N

这样当

• 协方差 > 0, 趋势向上，X 和 Y 正相关

• 协方差 < 0, 趋势向下，X 和 Y 负相关

• 协方差 ≈ 0, 无明显趋势，X 和 Y 不相关

最后把所计算的均值、方差、协方差汇总成协方差矩阵。

协方差矩阵

对于 2 维数据，它的协方差矩阵是 2×2 的对称矩阵。类比一下，

• 对于 5 维数据，它的协方差矩阵是 5×5 的对称矩阵。

• 对于 D 维数据，它的协方差矩阵是 D×D 的对称矩阵。

根据上面数据模式，我们计算出来他的协方差矩阵为

    [ 9, 4

      4, 3 ]

我们发现，

• 数据在 x 轴上的方差 9 大于数据在 y 轴上的方差 3，合理！

• X 和 Y 正相关，协方差为 4，合理！
  

5

我们知道矩阵其实就是线性转换，那么

    矩阵 × 向量 1 = 向量 2

就是把向量 1 线性转换成向量 2。

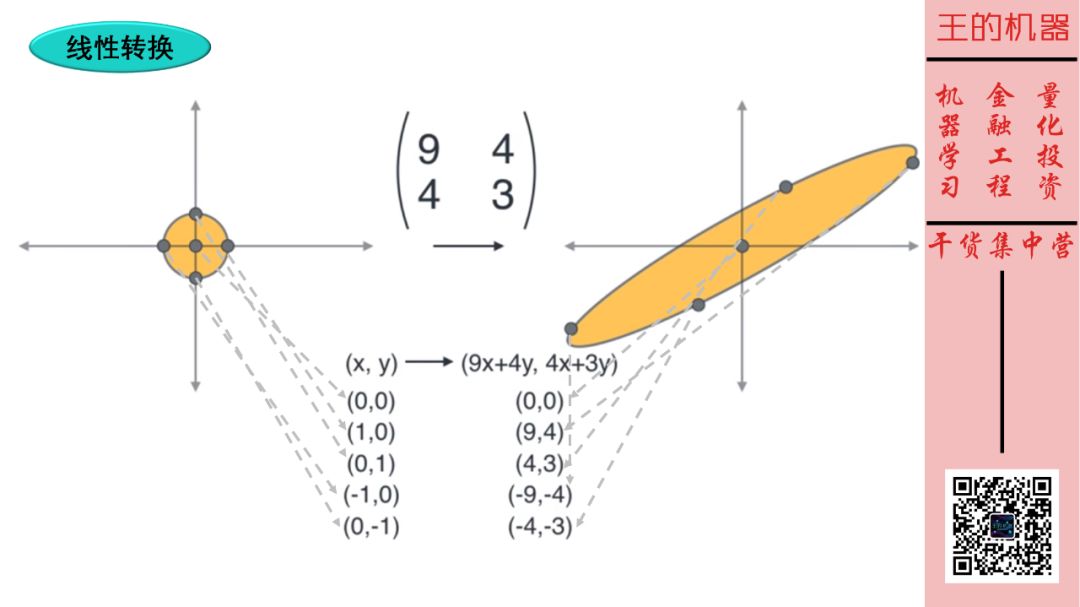
不懂？没关系，跟着上图，试着用矩阵 [9, 4; 4, 3] 来转换几个标准点

• (0, 0) → (0, 0)

• (1, 0) → (9, 4)

• (0, 1) → (4, 3)

• (-1, 0) → (-9, -4)

• (0, -1) → (-4, -3)

那么圆形被该矩阵转换成向上的椭圆形。

6

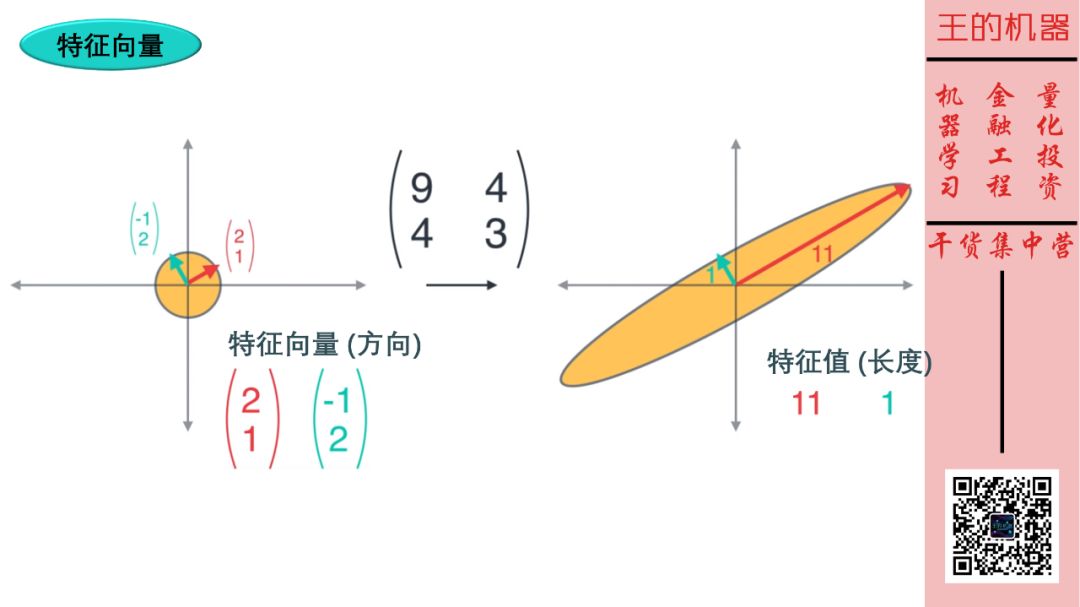
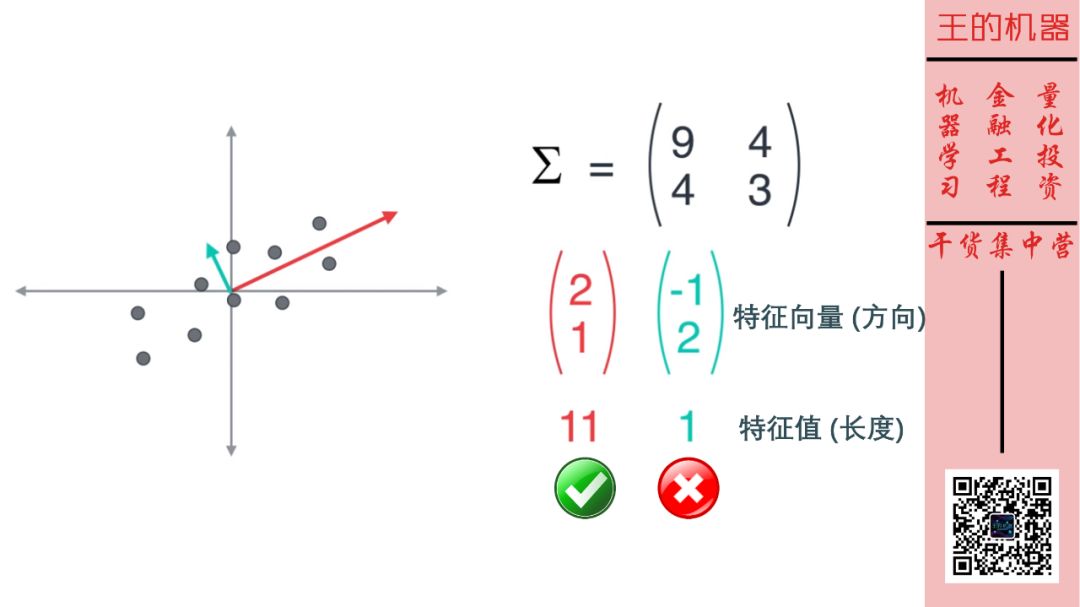
在以上线性转换中，有两个非常重要的向量，它们方向不变，长度改变。这样的向量称为特征向量，对应向量的长度称为特征值。如下图所示。

红色和青色向量是特征向量，它们方向不变。而黄色向量不是特征向量，它们方向变了。

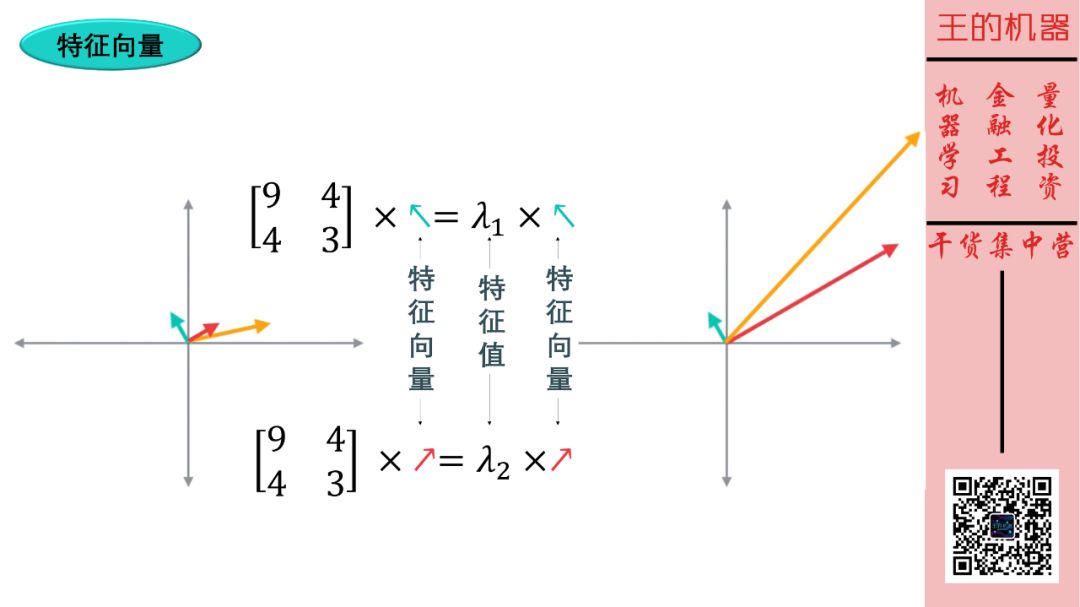
求特征向量和特征值的方法就不细说了，就是解一个方程

    矩阵 × 向量 = 常数 × 向量

你看，等式左边是用矩阵相乘将向量做了线性转化，而等式右边是用常数相乘将向量做了放缩 (没改变向量的方向哦)。

7

讲完特征向量和特征值后，我们可以介绍 PCA 的操作了，一句话，PCA 将数据投影到特征向量 (主成分) 上，而特征值代表数据投影后的方差大小。

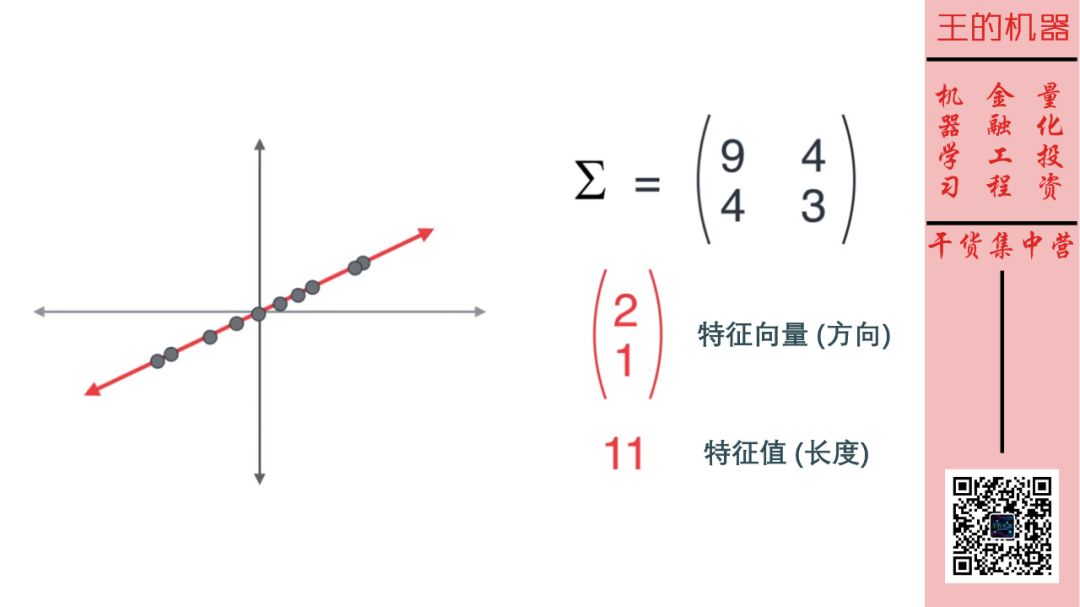
因此降维操作可是看成是选择特征值比较大的几个主成分作为特征。如上图，我们只保留了第一个主成分 (特征值 11)，而去除了第二个主成分 (特征值 1)。

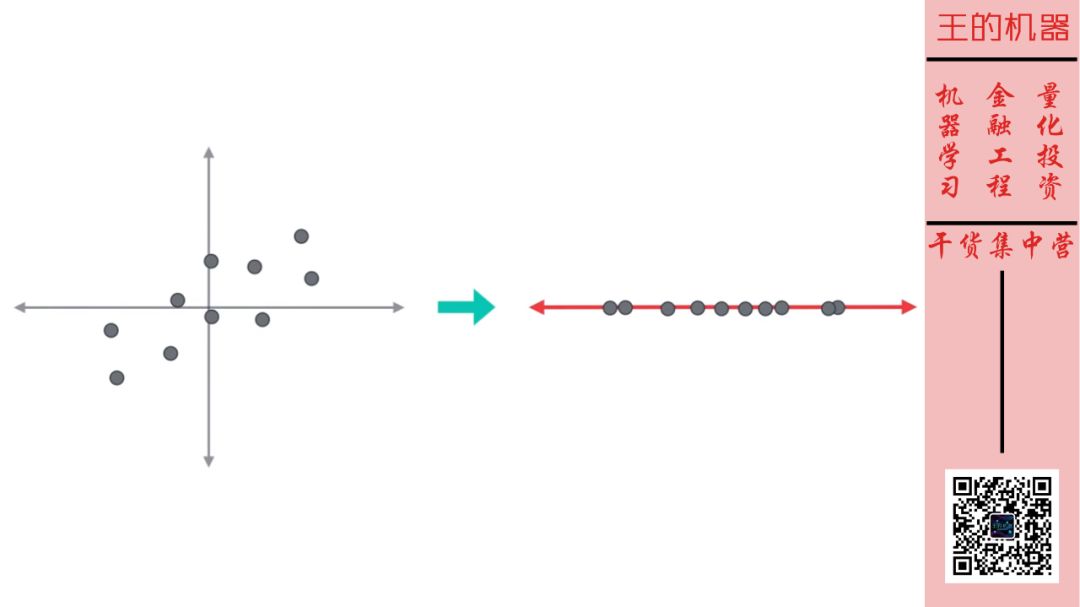
这样 2 维数据就变成了 1 维数据。因此第二个主成分的特征值 1 比第一个主成分特征值 11 小很多，那么将其去除不会丢失太多信息的。 从下面两图也可以看出。

总结

回到开始的场景，来总结一下 PCA 的完整操作。

1. 一开始我们有 5 维特征，分别是房间面积、房间个数、卧室个数、周边好学校个数和周边犯罪率。

   
   

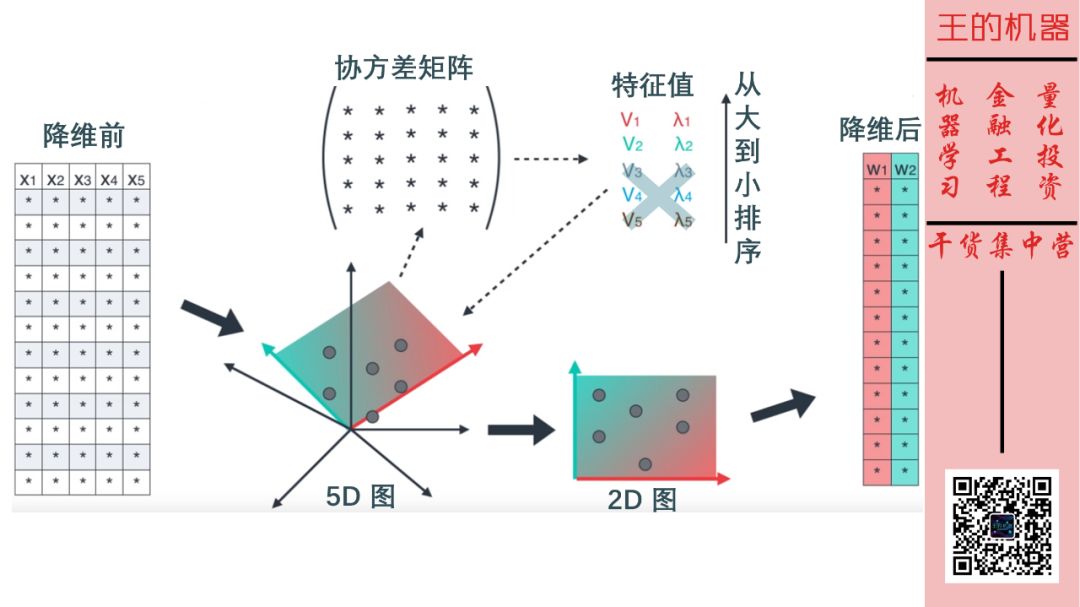
2. 这 5 维特征可以体现在一个 5D 图中，虽然我们无法精准的把它画出来。

   
   

3. 计算协方差矩阵，5 维特征得到 5×5 的对称矩阵。

   
   

4. 求出特征向量和特征值，将特征值从大到小排序，去除明显比较小 (这个需要点主观判断) 的，假设去除了后三个，保留了前两个。

   
   

5. 这 2 维特征可以体现在一个 2D 图中，我们人类终于可以可视化它了。

   
   

6. 当然原来「5 维特征的数据表」缩减成了「2 维特征的数据表」，希望这 2 维体现的是抽象的尺寸特征和环境特征，就像开头那张图一样。

觉得好就帮我传播这个看不懂算我输系列咯，谢谢大家！