机器学习(30)之线性判别分析(LDA)原理详解
微信公众号
关键字全网搜索最新排名
【机器学习算法】:排名第一
【机器学习】:排名第一
【Python】:排名第三
【算法】:排名第四
前言
在主成分分析(PCA)原理总结(机器学习(27)【降维】之主成分分析(PCA)详解)中对降维算法PCA做了总结。这里就对另外一种经典的降维方法线性判别分析(Linear Discriminant Analysis, 简称LDA)做一个总结。LDA在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用,因此我们有必要了解下它的算法原理。在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题模型。本文只讨论线性判别分析,因此后面所有的LDA均指线性判别分析。
LDA思想
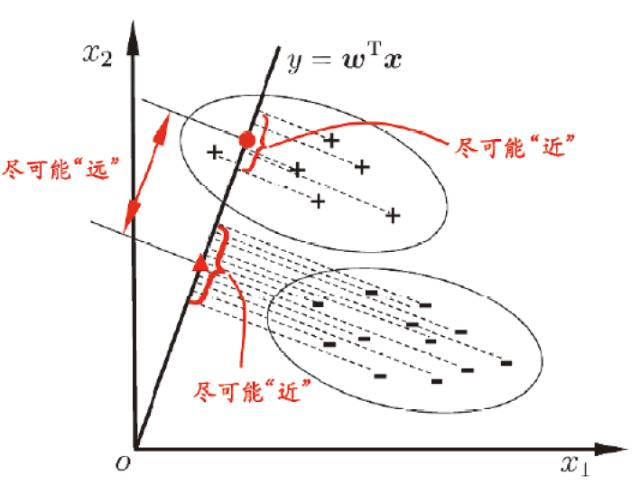
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的,这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”,如下图所示。 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
可能还是有点抽象,先看看最简单的情况。
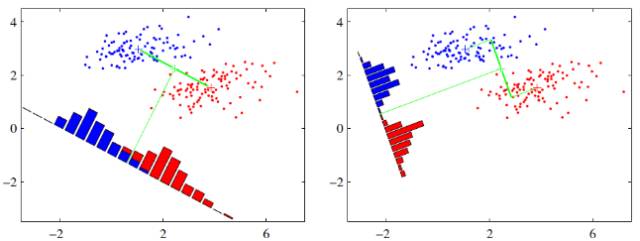
假设有两类数据,分别为红色和蓝色,如下图所示,这些数据特征是二维的,希望将这些数据投影到一维的一条直线,让每一种类别数据的投影点尽可能的接近,而红色和蓝色数据中心之间的距离尽可能的大。
上图中提供了两种投影方式,哪一种能更好的满足我们的标准呢?从直观上可以看出,右图要比左图的投影效果好,因为右图的黑色数据和蓝色数据各个较为集中,且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了,当然在实际应用中,数据是多个类别的,我们的原始数据一般也是超过二维的,投影后的也一般不是直线,而是一个低维的超平面。
LDA原理与流程
LDA与PCA
LDA用于降维,和PCA有很多相同,也有很多不同的地方,因此值得好好的比较一下两者的降维异同点。
相同点
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。
不同点
1)LDA是有监督的降维方法,而PCA是无监督的降维方法
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
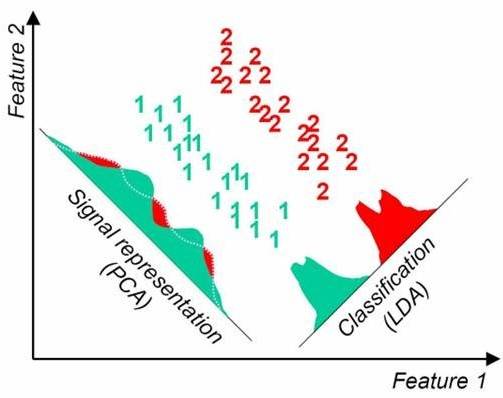
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。这点可以从下图形象的看出,在某些数据分布下LDA比PCA降维较优。
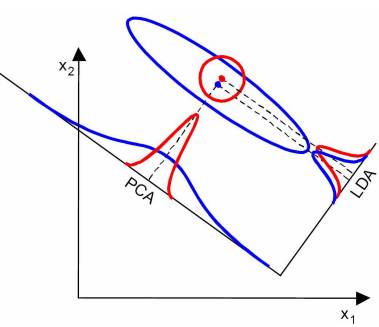
当然,某些某些数据分布下PCA比LDA降维较优,如下图所示:
LDA小结
LDA算法既可以用来降维,又可以用来分类,但是目前来说,主要还是用于降维。在进行图像识别相关的数据分析时,LDA是一个有力的工具。下面总结下LDA算法的优缺点。
优点
1)在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
2)LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
缺点
1)LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
2)LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
3)LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
4)LDA可能过度拟合数据。
欢迎分享给他人让更多的人受益

参考:
周志华《机器学习》
Neural Networks and Deep Learning by By Michael Nielsen
博客园
http://www.cnblogs.com/pinard/p/6244265.html
李航《统计学习方法》
Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
近期热文
干货 | 高盛:2017人工智能报告中文版(附PDF版下载)
想进微信机器学习交流1群
加微信:guodongwe1991
备注姓名-单位-研究方向
广告、商业合作
请加微信:guodongwe1991
12月23日,DAL的三位数据科学大牛将在中关村进行一场关于实用数据与人工智能的线下分享会。
活动主题:
成为超级人类,驯服人工智能
活动时间:
12月23日 14:00~17:00
活动地点:
中关村创业大街
扫码即可报名
前100名免费购票