【直观详解】什么是PCA、SVD

【直观详解】什么是PCA、SVD

在说明一个解释型内容的过程中，我一直坚信，带有思考的重复的是获取的知识的唯一捷径，所以会加入很多括号的内容，即另一种说法（从不同角度或其他称呼等），这样有助于理解。加粗的地方我也认为是比较重要的关键字或者逻辑推导，学习有一个途径就是划重点，做笔记。

1

What & Why PCA (主成分分析)

PCA，Principal components analyses，主成分分析。广泛应用于降维，有损数据压缩，特征提取和数据可视化。也被称为Karhunen-Loeve变换

从降维的方法角度来看，有两种PCA的定义方式，这里需要有一个直观的理解：什么是变换（线性代数基础），想整理一下自己线性代数的可以移步我的另一篇文章：【直观详解】线性代数的本质

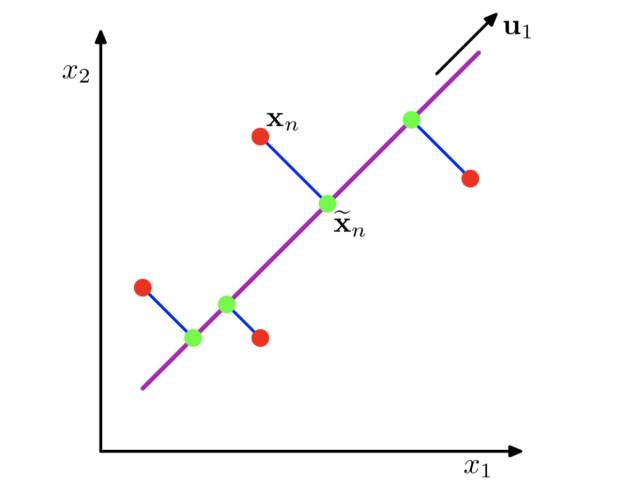
但是总的来说，PCA的核心目的是寻找一个方向（找到这个方向意味着二维中的点可以被压缩到一条直线上，即降维），这个方向可以：

• 最大化正交投影后数据的方差（让数据在经过变换后更加分散）

• 最小化投影造成的损失（下图中所有红线（投影造成的损失）加起来最小）

转自：机器学习算法与自然语言处理

完整内容请点击“阅读原文”