大白话深度学习中的Sigmoid函数

极市导读
Sigmoid函数是理解神经网络如何学习复杂问题的关键。这个函数也是学习其他函数的基础,这些函数可以为深度学习架构中的监督学习提供高效的解决方案。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
无论是自己实现一个神经网络,还是使用一个内置的库来学习神经网络,了解 Sigmoid函数的意义是至关重要的。Sigmoid函数是理解神经网络如何学习复杂问题的关键。这个函数也是学习其他函数的基础,这些函数可以为深度学习架构中的监督学习提供高效的解决方案。本文分为三个部分:
-
Sigmoid函数
-
线性与非线性可分性
-
为什么神经网络可以通过使用Sigmoid函数,作出复杂的决策边界
1. Sigmoid Function
1.1 Sigmoid函数的性质和恒等式
Sigmoid函数是 Logistic函数的一种特殊形式,通常用 σ (x)或 sig (x)来表示。如下所示:
Sigmoid 函数是一条 s 形曲线,如下图中的绿线所示。该图还显示了粉红色的导数图形:
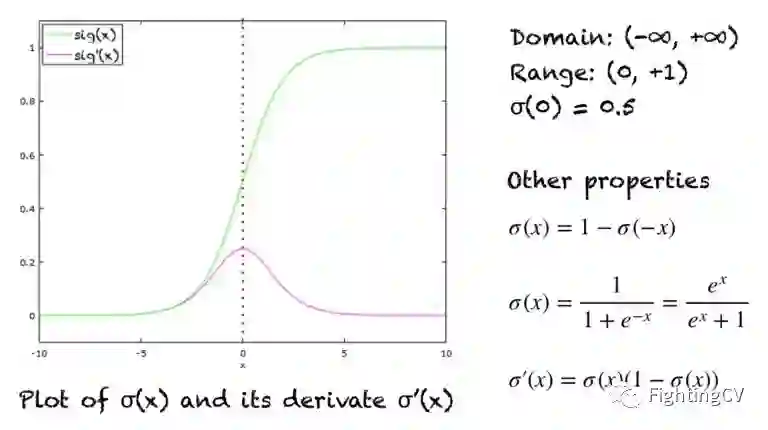
1.2 Sigmoid——压缩函数
Sigmoid函数也可以作为压缩函数,因为它的域是所有实数的集合,它的范围是(0,1)。因此,如果函数的输入是一个非常大的负数或非常大的正数,则输出总是介于0和1之间。在-∞和 + ∞之间的任何数字也是如此。
1.3 Sigmoid——激活函数
Sigmoid函数被用作神经网络中的激活函数。为了回顾什么是激活函数神经元,下面的图显示了激活函数神经元在神经网络的一个层中所起的作用。输入的加权和通过一个激活函数,这个输出作为下一层的输入。
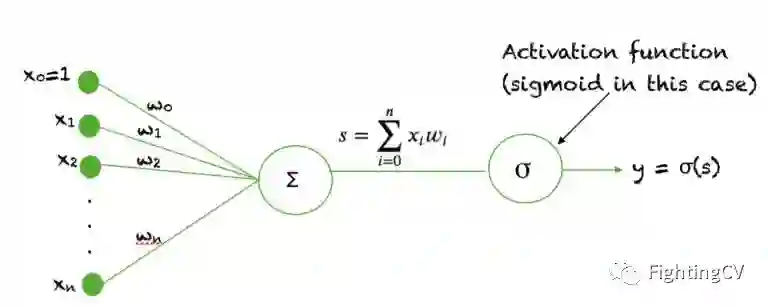
当一个神经元的激活函数是一个 Sigmoid函数时,这个单元的输出保证总是介于0和1之间。此外,由于 Sigmoid是一个非线性函数,这个单元的输出将是一个非线性函数的加权和的输入。这种以Sigmoid函数为激活函数的神经元被称为sigmoid unit 。
2. 线性与非线性可分性?
假设我们有一个典型的分类问题,我们在空间中有一组点,每个点被分配一个类标签。如果一条直线(或 n 维空间中的一个超平面)可以将这两类分开,那么我们就有一个线性可分问题。另一方面,如果一条直线不足以划分这两类,那么我们就有一个非线性可分问题。下图显示了二维空间中的数据。每个点被分配一个红色或蓝色的类标签。左图显示了一个线性可分问题,该问题需要一个线性边界来区分两类问题。右图显示了一个非线性可分问题,需要一个非线性决策边界。
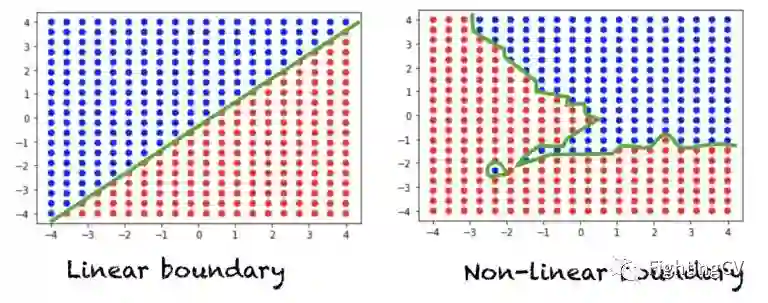
对于三维空间,线性决策边界可以用平面方程来描述。对于 n 维空间,线性决策边界由超平面方程描述。
3. 为什么 Sigmoid函数在神经网络中很重要?
如果我们在神经网络中使用线性激活函数,那么这个模型只能学习线性可分问题。然而,只要在隐藏层中增加一个隐藏层和一个 Sigmoid激活函数,神经网络就可以很容易地学习一个非线性可分问题 。使用非线性函数产生非线性边界,因此,Sigmoid函数可以用于神经网络学习复杂的决策函数。
在神经网络中,可以用作激活函数的非线性函数必须是一个单调递增 的函数。例如,sin (x)或 cos (x)不能用作激活函数。另外,激活函数应该定义为任意处 ,并且在实数空间中任意处都是连续的 。这个函数还要求在整个实数空间上是可微 的。
通常,反向传播算法使用梯度下降法学习神经网络的权重。为了得到这个算法,需要对激活函数进行求导数。而由于Sigmoid函数是单调的,连续的,到处可微的 ,再加上它的导数可以用它自己来表示 的特性,使得当使用反向传播算法时,很容易推导出学习神经网络中的权重的更新方程。
如果觉得有用,就请分享到朋友圈吧!
公众号后台回复“CVPR21检测”获取CVPR2021目标检测论文下载~

# CV技术社群邀请函 #

备注:姓名-学校/公司-研究方向-城市(如:小极-北大-目标检测-深圳)
即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群
每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~



