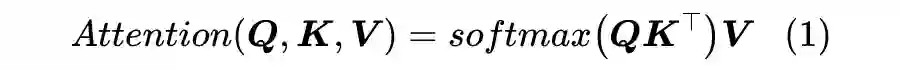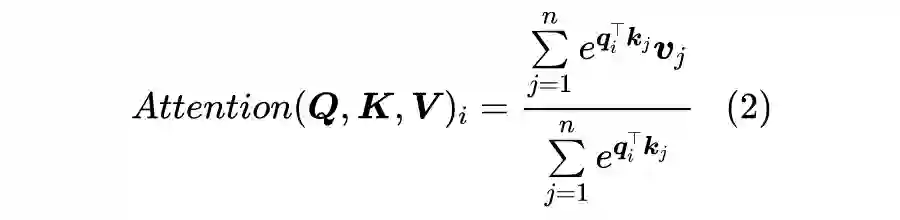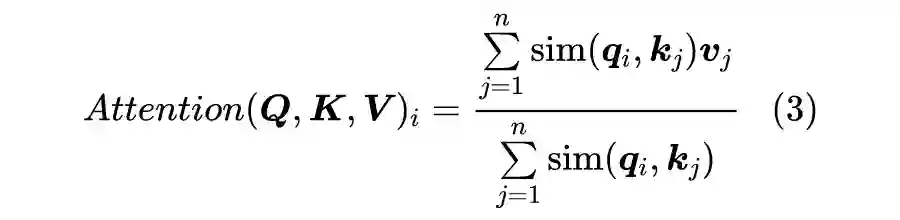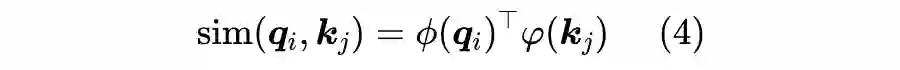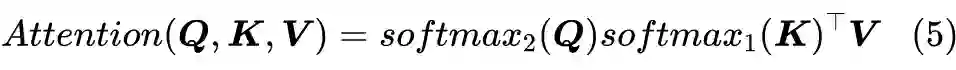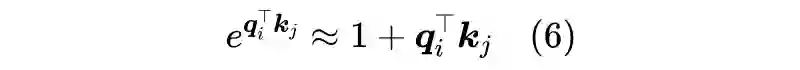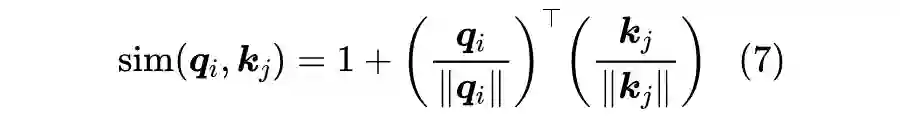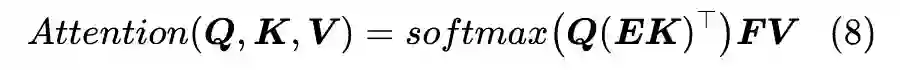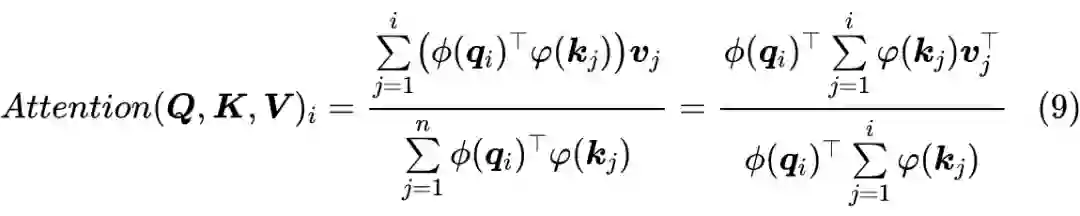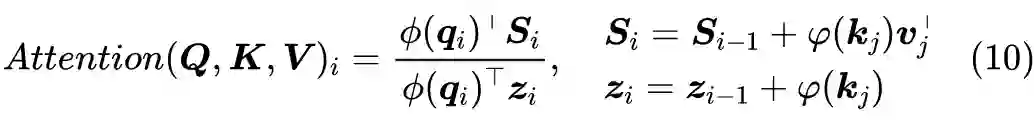线性Attention的探索：Attention必须有个Softmax吗？

©PaperWeekly 原创 · 作者｜苏剑林

单位｜追一科技

研究方向｜NLP、神经网络

众所周知，尽管基于 Attention 机制的 Transformer 类模型有着良好的并行性能，但它的空间和时间复杂度都是 级别的，n 是序列长度，所以当 n 比较大时 Transformer 模型的计算量难以承受。

近来，也有不少工作致力于降低 Transformer 模型的计算量，比如模型剪枝、量化、蒸馏等精简技术，又或者修改 Attention 结构，使得其复杂度能降低到 甚至 。

前几天笔者读到了论文 Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention  [1]  ，了解到了线性化 Attention （Linear Attention）这个探索点，继而阅读了一些相关文献，有一些不错的收获，最后将自己对线性化 Attention 的理解汇总在此文中。

Attention

当前最流行的 Attention 机制当属 Scaled-Dot Attention [2] ，形式为：

这里的 ，简单起见我们就没显式地写出 Attention 的缩放因子了。

本文我们主要关心 Self Attention 场景，所以为了介绍上的方便统一设 ，一般长序列场景下都有 （BERT base 里边 d=64）。

相关解读可以参考笔者的一文读懂「Attention is All You Need」| 附代码实现，以及它的一些改进工作也可以参考突破瓶颈，打造更强大的 Transformer [3] 、Google 新作 Synthesizer：我们还不够了解自注意力，这里就不多深入介绍了。

1.1 摘掉Softmax

读者也许想不到，制约 Attention 性能的关键因素，其实是定义里边的 Softmax！事实上，简单地推导一下就可以得到这个结论。

这一步我们得到一个 的矩阵，就是这一步决定了 Attention 的复杂度是 ；如果没有 Softmax，那么就是三个矩阵连乘 ，而矩阵乘法是满足结合率的，所以我们可以先算 ，得到一个 的矩阵，然后再用 左乘它，由于 ，所以这样算大致的复杂度只是 （就是 左乘那一步占主导）。

也就是说，去掉 Softmax 的 Attention 的复杂度可以降到最理想的线性级别 ！这显然就是我们的终极追求：Linear Attention，复杂度为线性级别的 Attention。所以，本文的主题就是探究摘掉 Softmax 后的线形 Attention。

1.2 一般的定义

问题是，直接去掉 Softmax 还能算是 Attention 吗？它还能有标准的 Attention 的效果吗？为了回答这个问题，我们先将 Scaled-Dot Attention 的定义（1）等价地改写为（本文的向量都是列向量）。

所以，Scaled-Dot Attention 其实就是以 为权重对 做加权平均。所以我们可以提出一个 Attention 的一般化定义：

也就是把 换成 的一般函数 ，为了保留 Attention 的相似特性，我们要求 恒成立。也就是说，我们如果要定义新式的 Attention，那么要保留式（3）的形式，并且满足 。

这种一般形式的 Attention 在 CV 中也被称为 Non-Local 网络，来自文章 Non-local Neural Networks [4] 。

几个例子

如果直接去掉 Softmax，那么就是 ，问题是内积无法保证非负性，所以这还不是一个合理的选择。下面我们简单介绍几种可取的方案。

值得指出的是，下面介绍的这几种 Linear Attention，前两种只做了 CV 的实验，第三种是笔者自己构思的，所以都还没有在 NLP 任务上做过什么实验，各位做模型改进的 NLPer 们就有实验方向了。

2.1 核函数形式

一个自然的想法是：如果 的每个元素都是非负的，那么内积自然也就是非负的。为了完成这点，我们可以给 各自加个激活函数 ，即：

其中 是值域非负的激活函数。本文开头提到的论文 Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention [5]  选择的是 。

非要讲故事的话，式（4）可以联想到“核方法（kernal method）”，尤其是 时 就相当于一个核函数，而 就是通过核函数所定义的内积。

这方面的思考可以参考论文 Transformer dissection: An unified understanding for transformer’s attention via the lens of kernel [6] ，此处不做过多延伸。

2.2 妙用Softmax

另一篇更早的文章 Efficient Attention: Attention with Linear Complexities  [7]  则给出了一个更有意思的选择。它留意到在 中， ，如果“ 在 d 那一维是归一化的、并且 在 n 那一维是归一化的”，那么 就是自动满足归一化了，所以它给出的选择是：

其中 分别指在第一个（n）、第二个维度（d）进行 Softmax 运算。也就是说，这时候我们是各自给 加 Softmax，而不是 算完之后才加 Softmax。

其实可以证明这个形式也是式（4）的一个特例，此时对应于 ，读者可以自行推导一下。

2.3 自己的构思

在这里，笔者给出自己的一种构思。这个构思的出发点不再是式（4），而是源于我们对原始定义（2）的近似。由泰勒展开我们有：

如果 ，那么就可以保证右端的非负性，而从可以让 。到这里读者可能已经想到了，想要保证 ，只需要分别对 做 归一化。所以，笔者最终提出的方案就是：

这不同于形式（4），但理论上它应该是最接近原始的 Scaled-Dot Attention 了。

相关工作

通过修改 Attention 的形式来降低它的计算复杂度，相关的工作有很多，这里简要列举一些。

3.1 稀疏Attention

我们之前介绍过 OpenAI 的 Sparse Attention，通过“只保留小区域内的数值、强制让大部分注意力为零”的方式，来减少 Attention 的计算量。经过特殊设计之后，Attention 矩阵的非 0 元素只有 个，所以理论上它也是一种线性级别的 Attention。类似的工作还有 Longformer。

但是很明显，这种思路有两个不足之处：

1. 如何选择要保留的注意力区域，这是人工主观决定的，带有很大的不智能性；

2. 它需要从编程上进行特定的设计优化，才能得到一个高效的实现，所以它不容易推广。

3.2 Reformer

Reformer 也是有代表性的改进工作，它将 Attention 的复杂度降到了 。

某种意义上来说，Reformer 也是稀疏 Attention 的一种，只不过它的稀疏 pattern 不是事先指定的，而是通过 LSH（Locality Sensitive Hashing）技术（近似地）快速地找到最大的若干个 Attention 值，然后只去计算那若干个值。

此外，Reformer 通过构造可逆形式的 FFN（Feedforward Network）替换掉原来的 FFN，然后重新设计反向传播过程，从而降低了显存占用量。

所以，相比前述稀疏 Attention，Reformer 解决了它的第一个缺点，但是依然有第二个缺点：实现起来复杂度高。要实现 LSH 形式的 Attention 比标准的 Attention 复杂多了，对可逆网络重写反向传播过程对普通读者来说更是遥不可及。

3.3 Linformer

跟本文所介绍的 Linear Attention 很相似的一个工作是 Facebook 最近放出来的 Linformer，它依然保留原始的 Scaled-Dot Attention 形式，但在进行 Attention 之前，用两个 的矩阵 分别对 进行投影，即变为：

这样一来， 就只是一个 的矩阵，而作者声称对于哪怕对于很大的序列长度 n，m 也可以保持为一个适中的常数，从而这种 Attention 也是线性的。

但是，笔者认为“对于超长序列 m 可以保持不变”这个结论是值得质疑的，原论文中对于长序列作者只做了 MLM 任务，而很明显 MLM 并不那么需要长程依赖，所以这个实验没什么说服力。因此，Linformer 是不是真的 Linear，还有待商榷。

3.4 自回归生成

Linformer 的另一个缺点是 这两变直接把整个序列的信息给“糅合”起来了，所以它没法简单地把将来信息给 Mask 掉（Causal Masking），从而无法做语言模型、Seq2Seq 等自回归生成任务，这也是刚才说的原作者只做了 MLM 任务的原因。

相比之下，本文介绍的几种 Linear Attention 都能做到这一点。以式（3）和式（4）为例，如果要 Mask 掉未来信息，那么只需要把求和 改为 ：

实现上式有两种方式：第一方式是设 以及 ，我们有：

这说明这种 Attention 可以作为一个 RNN 模型用递归的方式实现，它的空间复杂度最低，但是要串性计算，适合预测解码时使用；第二种是直接将 做外积，得到一个 的矩阵，然后对 n 那一维执行 运算，这样就一次性得到 了，它的速度最快，但空间占用最大，适合训练时使用。

3.5 下采样技术

从结果上来看，Linformer 的 就是将序列变短（下采样）了，而将序列变短的一个最朴素的方法就是 Pooling 了，所以笔者之前也尝试过把 Pooling 技术引入到 Transformer 中去。

近来也有类似的工作发出来，比如IBM的PoWER-BERT: Accelerating BERT Inference via Progressive Word-vector Elimination [8] 和 Google 的 Funnel-Transformer: Filtering out Sequential Redundancy for Efficient Language Processing [9] 。

除了 Pooling 之外，其实还有其他的下采样技术，比如可以通过 stride > 1 的一维卷积来实现，基于这个思路，或许我们可以把 FFN 里边的 Position-Wise 全连接换成 stride > 1 的一维卷积？总之这方面应该也能玩出很多花样来，不过跟 Linformer 一样，这样糅合之后做自回归生成就很难了。

文章小结

本文介绍了一些从结构上对 Attention 进行修改从而降低其计算复杂度的工作，其中最主要的 idea 是去掉标准 Attention 中的 Softmax，就可以使得 Attention 的复杂度退化为理想的 级别（Linear Attention）。

相比于其他类似的改进结构的工作，这种修改能在把复杂度降到 的同时，依然保留所有的 “token-token” 的注意力，同时还能保留用于做自回归生成的可能性。

参考链接

[1] https://arxiv.org/abs/2006.16236

[2] https://arxiv.org/abs/1706.03762

[3] https://kexue.fm/archives/7325

[4] https://kexue.fm/archives/1711.07971

[5] https://arxiv.org/abs/2006.16236

[6] https://arxiv.org/abs/1908.11775

[7] https://arxiv.org/abs/1812.01243

[8] https://arxiv.org/abs/2001.08950

[9] https://arxiv.org/abs/2006.03236

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。