用Attention玩转CV，一文总览自注意力语义分割进展

机器之心专栏

作者：李夏

本文总结近两年语义分割领域对 attention 和“低秩”重建机制的探索，并介绍笔者被 ICCV 2019 接收为 Oral 的工作：Expectation-Maximization Attention Networks for Semantic Segmentation（ 代码已开源： github.com/XiaLiPKU/EMANet ）。 注： 本文中的 attention 仅指 self-attention，不涉及 soft-attention。

Attention 机制继在 NLP 领域取得主导地位^[1]之后，近两年在 CV 领域也开始独领风骚。率先将之引入的是 Kaiming He 组的 Nonlocal^[2]。此后层出不穷的文章，引发了一波研究 attention 机制的热潮。

仅2018年，在语义分割领域就有多篇高影响力文章出炉，如 PSANet^[3]，DANet^[4]，OCNet^[5]，CCNet^[6]，以及今年的Local Relation Net^[7]。此外，针对 Attention 数学形式的优化，又衍生出A2Net^[8]，CGNL^[9]。而 A2Net 又开启了本人称之为“低秩”重建的探索，同一时期的SGR^[10]，Beyonds Grids^[11]，GloRe^[12]，LatentGNN^[13] 都可以此归类。

上述四文皆包含如下三步：1.像素到语义节点映射 2.语义节点间推理 3.节点向像素反映射。其中，step 2的意义尚未有对比实验验证，目前来看，step 1 & 3 构成的对像素特征的低秩重建发挥了关键作用。关于如何映射和反映射，又有了 APCNet^[14]  和笔者的 EMANet^[15]  等相关工作。

Nonlocal

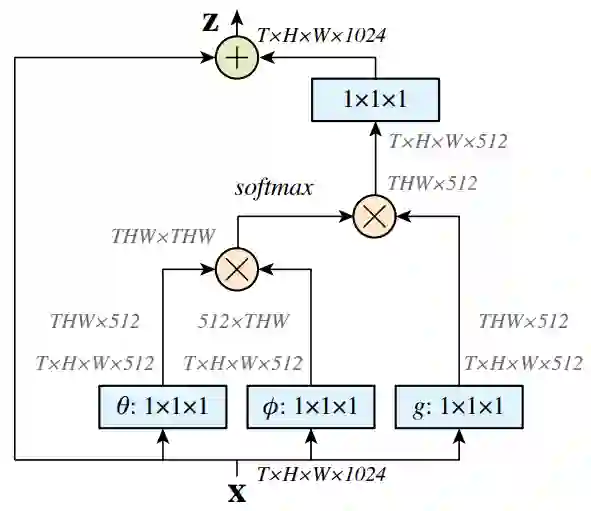
Nonlocal^[2]中的核心操作为：

其中  ，  是像素个数，  是像素特征维度（通道数），  计算  和  之间的相关度（或称“能量”），  对  进行变换。可以看作对  的加权平均得到 ，作为对  的重构，这里权重为  。

关于  和  的选择，作者列出了多个选项，并最终选择了

的形式，其中  分别对应  NLP Transformer  里的 query ， key 和 value 。此外，  经过  卷积后和  相加，作为 Non-local 模块的输出。最后结构图如下：

Non-local Block

其实，这里  和  的具体选择，对效果影响不大。在笔者做过的语义分割实验中， query 和 key 共享，节省一些参数，并且这样计算出的  是个对称矩阵。甚至可以考虑将 转换省略，直接用  本身计算，而把  卷积放在模块之前之后，这样的效果也不逊色。当然，不同的任务应该对应于不同的最优选项。今年 arxiv 有篇文章^[16]详细对比分析了这些细节在不同任务中的影响。笔者认为此处最关键的是加权平均，而非 转换。

这里  计算时，只考虑了像素的特征，而没有考虑相对位置。倘若也将像素坐标位置  考虑进来，其实就是全图版的 MeanShift Filter，一种经典的保边滤波算法。Nonlocal 还可以溯源到经典的 Non-local means 和 BM3D。其功效也来源于此，即高维  feature map 里存在大量的冗余信息，该类算法可以消除大量噪音。Kaiming 组的另一篇文章^[17]分析了 Nonlocal 对模型鲁棒性的提升，考虑到上述的去噪效果，这个结论是显而易见的。效果如下：

a. 原图 b. Feature map c. Feature map after Nonlocal

Other Attention Models

PSANet^[3] 和  Nonlocal  最大的区别在于，相关度矩阵  的计算。对于像素  ，其相关度向量  ，通过施加在  上的两个  卷积得到，即由  变为  ，只和 query 及相对位置相关。此外，PSANet  包含两路  attention ，相当于 transformer 中的两个 head 。两路分别起到  collect  和 distribute  的作用。

而 DANet^[4]，是把 Nonlocal 操作视为 spatial attention，以此引出了 channel attention ，两路融合。OCNet^[5]，则是将 object context (spatial attention) 和卷积强强联合，分别捕捉全局和局部信息，并在多个数据集上取得很高的精度。

Nonlocal 对于每个  的计算，都要在全图上进行，因此复杂度为  。CCNet^[6]将全图计算分解为两步，一步是按行计算，一步是按列计算。类比于将矩阵  分解为  。因此 CCNet 复杂度为  。

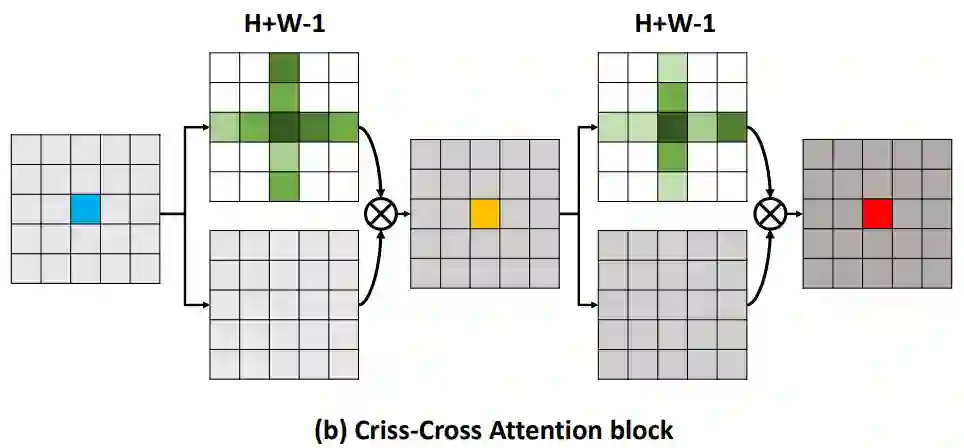
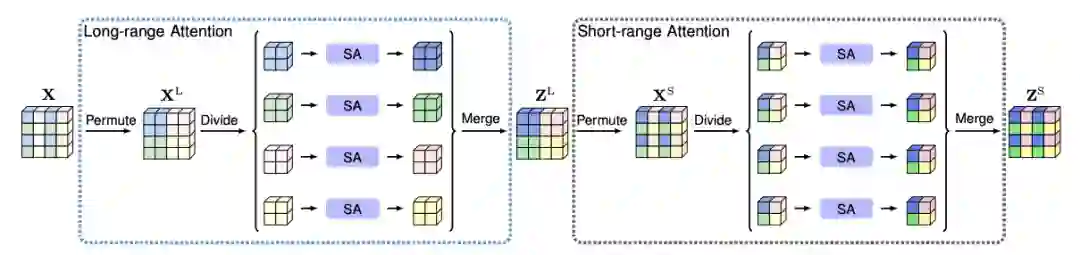
PKU兄弟实验室的 ISA^[18]也是将 attention map 的全图计算分解为两步：第一步长距离attention ，第二步短距离。中间夹着一步 permute 操作。其实类似组卷积- shuffle -组卷积的过程，思路上顺承 IGCV^[19]，其复杂度也是 。

ISA

Oxford的DGMN^[20]则通过MC采样，使每个像素计算attention所需的参考像素从  降为  。此外，采样过程可导，可以和网络同步学习，且  个参考像素各自对应不同的变换  。DGMN把复杂度降为  ，且精度超过Nonlocal。

DGMN

另一种减少计算量的方法，是将 attention 的全图计算改为窗口内计算。MeanShift 若限制窗口大小，便是 Bilateral Filter，即每个像素的特征，更新为邻域内其他像素的加权平均。权重由特征相似度和空间距离计算而来。而 MeanShift 也被证明等价于迭代至收敛的Bilateral Filter^[21]。

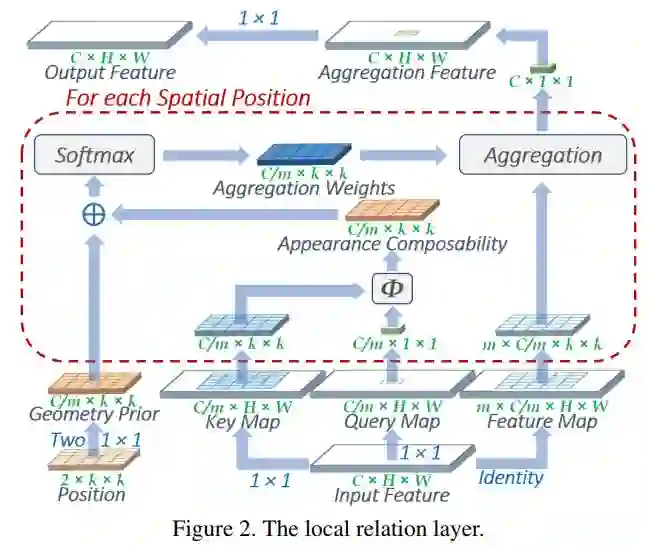
MSRA 的 Local Relation Net^[7]设计了类似 Bilateral Filter 的操作，在特征相关度计算上使用了标准的 query，key，value 三元组，在空间相关度上设计了Geometry Prior。并且大胆地用这一算子替代了  卷积。其节省参数的同时，还具有旋转等变性。整个结构下来有 Transformer 的感觉，即不用 RNN，CNN来收集 context 信息，而是用 attention 来做。至于为什么起效，笔者更想归根到 Bilateral Filter 本身的效果，即保边滤波，起到了保持类间方差的同时，减少类内方差的效果。

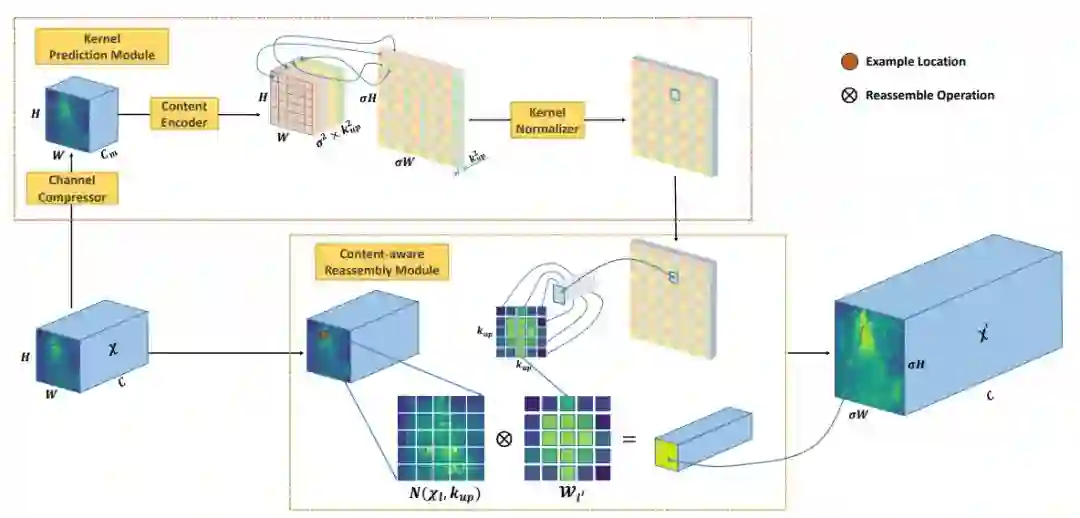
MMLab 的 CARAFE^[22]，用来进行特征上采样。其计算方式也是用窗口内像素特征的特征加权平均。其特殊之处在于，用于加权的权重是学习出来的，通过对特征变换、pixelshuffle上采样和通道归一化得到。

其实关于选择 global 还是 local 的问题，NLP 领域已经有好多研究，详见苏剑林的博文 《为节约而生：从标准Attention到稀疏Attention》。两个领域的研究，其实都在做类似的事情。

注释：本节所提及文章各有其出发点和独到之处，这里仅简单统一到一个框架下，并总结共通点。具体分析未免有缺失和差池，各文章精妙之处，还需参考其他博文。

A2Net and CGNL

NUS 的 A2Net^[8] 和 百度的 CGNL^[9] 另辟蹊径，从另一个角度优化了 Nonlocal 的复杂度。

Nonlocal 高昂的复杂度 成为制约其应用的关键瓶颈。我们可以重新审视下公式(2)

其中 ， ， 。因此，两步矩阵乘法计算量都是 。使用下乘法结合律，先算后两者的乘积，便可以得到  的复杂度。由于 ，复杂度减少了整整一个量级。再加入 ，便可以得到：

由于  的原因，两式并不完全等价。但是对于 deep learning 来说，两者的 capacity 是近似的。其实，一般地，  和  的维度被设定为小于  的，如前两者64，后者512。这里我们将前者的维度记为  。则 Nonlocal 和 A2Net 复杂度分别为 和  。

那么，如何从直觉上理解公式 (4) 呢？  里得到的是一个  的矩阵，可以看做是  个描述子，表达整个 feature map 中的关键概念。而 表示的是从  个像素到  个描述子的映射关系，可以看作像素特征加权平均得到了描述子，权重就是这个映射矩阵。  则反之，作为权重，将描述子加权平均，得到重构后的像素特征。

GloRe and so on

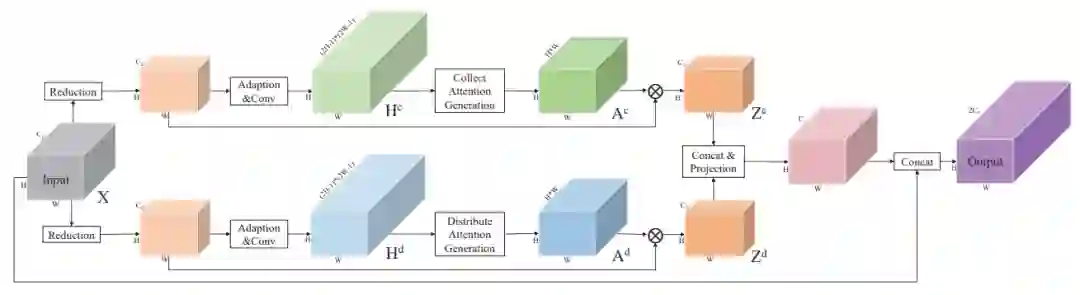
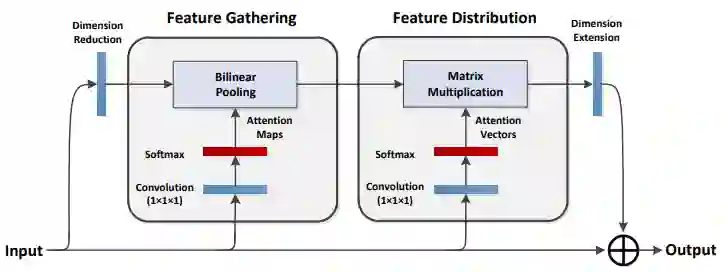
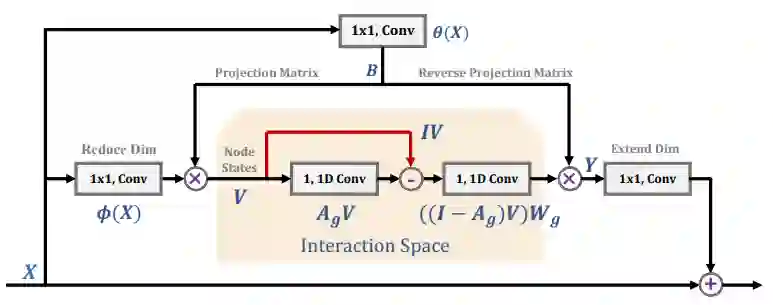
在 A2Net 基础上，Yunpeng Chen 继续做出了 GloRe^[12]。相比于 A2Net，GloRe 在映射 ( ) 和反映射 ( ) 之间插入了一步 GCN 的操作，使  的描述子矩阵内部交互和更新。GCN 的具体实现是两步  卷积。此外，作者发现  和  其实可以共享，即下图中的B，结论和上文中本人所言 query 和 key 共享一致。

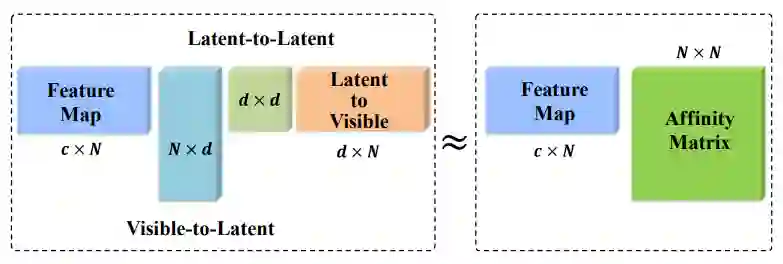
其实，和 GloRe 同一时期的相关工作还有 SGR^[10], Beyonds Grids^[11] 和 LatenGNN^[13]。它们都采取三步走的策略，即映射、GCN 和反映射。他们的区别在于每一步的具体操作。

四篇文章在 GCN 步骤各有设计。不过，目前为止，没有看到任何公开的 ablation study 证明第二步 GCN 有效果，自己复现的部分实验，也没有跑出 GCN 有增益的结果。所以，只能暂且认为关键还是在于映射和反映射。

那么，映射和反映射，为何能表现突出呢？这里只说一下自己对语义分割这个任务的分析。我们用来抽取 Feature 用的 ResNet，在 ImageNet 千类数据集上训练，因此特征维度至少 1000 维。而分割问题少则 20 类左右，多也不超过几百类。使用过千维的特征，显然是过参数化了。

对高维数据分类是低效的，因为高维空间中分类边界过于复杂。而映射反映射的流程，其实是对特征的一个低秩重构，使得高维空间中的特征重新分布到低维流形上，便于后续的分类。其实，A2Net 在 ImageNet 上也证明了自己的价值，这说明不只是分割问题合适，类似的一系列任务，都适用这种映射-反映射模块。

上述的几篇文章，映射和反映射矩阵，多是通过  卷积学习到的。其实，最常见的池化-上采样，也属于一种超级简化的映射-反映射范式。PSPNet 中的 PPM 和 DeeplabV3 中的 GAP 带来的效益，也可由这个角度进行一定的解释。SIAT-MMLAB 的 APCNet^[14]，也属于这一范式的一个具体结构。其 ACM 模块的映射步骤用池化，反映射用学习到的反映射矩阵 (Global-guided Local Affinity)。此外，APCNet 和上述的 Beyonds Grid 都用了多路并行，每路用不同的  ，来进行不同程度的稀疏重建。

EMANet

本文认为，映射的关键，在于寻找一组“最合适”的描述子，即论文中的“基”。这组基最好具有如下的几条性质：1. 具有代表性 2. 数量少 3. 互不相似。性质1能保证重构后的 feature map 能够最大限度地还原有效信息；性质2则可以保证重构的低秩性，使重构后的特征处在高维空间中的低维流形中；性质3则是在性质2的约束下，尽可能达到性质1的保证。使用池化，即简单下采样的，得到的基充分满足性质2；但互相之间仍十分相似，因此性质3不满足；小物体下采样后可能会信息丢失，因此性质1也仅仅能对大物体满足。

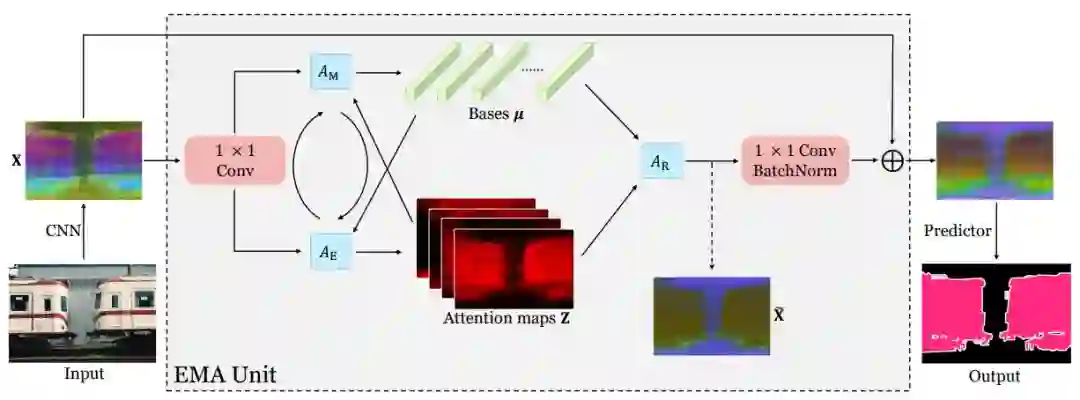
笔者被ICCV 2019收录为Oral的论文 EMANet^[23]，提出了用 EM 算法来求解映射和反映射。EM 算法用于求解隐变量模型的最大似然解。这里把隐变量视为映射矩阵，模型参数即为  个描述子。E步更新映射矩阵  ，M步更新描述子  。  次迭代后，用映射矩阵的转置（以及归一化）作为反映射矩阵，重构特征图。

EM 本身保证收敛到似然函数的局部最大值，因此 EM 算法迭代而出的描述子和映射关系，相对于简单地用网络学习到的，更能保证满足性质1；性质2可以通过设置较小的  来满足；而性质3，则可通过良好的描述子迭代初始化来做到。EMANet 的解读见笔者的另一篇文章：期望最大化注意力网络 EMANet 详解。

此处，我们可以考虑下 EMANet 和 A2Net 的关联。将公式(4)摘抄下来：

如果我们将其中的  和  的参数共享，并将 和  记作  。那么，  和  无异；而  就相当于  和  迭代一次。因此，A2-Block 可以看作 EMAU 的特殊例子，它只迭代一次 EM，且  由反向传播来更新。而 EMAU 迭代  步，用滑动平均来更新  。

在实验中，将 Nonlocal、A2Net 和 EMANet 中的模块在PASCAL VOC上作简单的对比实验。EMANet 仅迭代一次时分数与 Nonlocal 和 A2Net 无显著差异，符合上文对 Nonlocal 和 A2Net 的分析和对比。而 EMANet 在迭代多次时，性能可以有显著的提升。

总结

本文抛开 glocal context 的观点，重新从传统算法的角度出发，对上述文章作了重新的思考总结。回顾而来，所谓最新的成果，不过是站在了先贤的肩膀上，在深度学习的形式上进行了探索。追本溯源，笔者本人也不过是经典算法 EM 的搬运工。借此，向鼎力帮助我的三位师兄（Zhisheng Zhong，Jianlong Wu和Yibo Yang）和两位导师（Zhouchen Lin, Hong Liu）致敬。

感谢Qijie、大大拉头的仔细审稿。还要感谢《EM 算法的九层境界》的作者史博和科学空间苏剑林，他们的博文对我有很大的启发。

参考

1. Attention is All You Need https://arxiv.org/abs/1706.03762

2. Non-local Neural Networks https://arxiv.org/pdf/1711.07971.pdf

3. PSANet: Point-wise Spatial Attention Network for Scene Parsing https://hszhao.github.io/papers/eccv18_psanet.pdf

4. Dual Attention Network for Scene Segmentation https://arxiv.org/abs/1809.02983

5. OCNet: Object Context Network for Scene Parsing https://arxiv.org/abs/1809.00916

6. CCNet: Criss-Cross Attention for Semantic Segmentation https://arxiv.org/abs/1811.11721

7. Local Relation Networks for Image Recognition https://arxiv.org/abs/1904.11491

8. A2 -Nets: Double Attention Networks https://papers.nips.cc/paper/7318-a2-nets-double-attention-networks.pdf

9. Compact Generalized Non-local Network https://arxiv.org/abs/1810.13125

10. Symbolic Graph Reasoning Meets Convolutions https://pdfs.semanticscholar.org/4959/7c2c8d65f4d3b817aabfa31f16f3791be974.pdf

11. Beyond Grids: Learning Graph Representations for Visual Recognition https://www.biostat.wisc.edu/~yli/preprints/yin_nips2018_camera_ready.pdf

12. Graph-Based Global Reasoning Networks http://openaccess.thecvf.com/content_CVPR_2019/papers/Chen_Graph-Based_Global_Reasoning_Networks_CVPR_2019_paper.pdf

13. LatentGNN: Learning Efficient Non-local Relations for Visual Recognition https://arxiv.org/abs/1905.11634

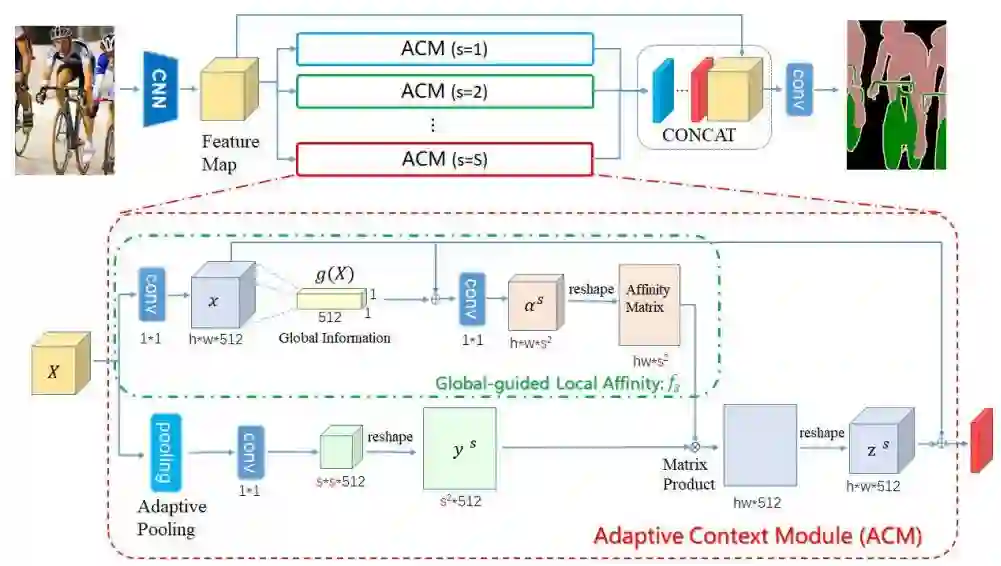
14. Adaptive Pyramid Context Network for Semantic Segmentation http://openaccess.thecvf.com/content_CVPR_2019/papers/He_Adaptive_Pyramid_Context_Network_for_Semantic_Segmentation_CVPR_2019_paper.pdf

15. Expectation-Maximization Attention Networks for Semantic Segmentation https://arxiv.org/abs/1907.13426

16. An Empirical Study of Spatial Attention Mechanisms in Deep Networks https://arxiv.org/abs/1904.05873

17. Feature Denoising for Improving Adversarial Robustness https://arxiv.org/abs/1812.03411

18. Interlaced Sparse Self-Attention for Semantic Segmentation https://arxiv.org/abs/1907.12273

19. Interleaved Group Convolutions for Deep Neural Networks https://arxiv.org/abs/1707.02725

20. Dynamic Graph Message Passing Networks https://arxiv.org/abs/1908.06955

21. A General Framework for Bilateral and Mean Shift Filtering https://people.csail.mit.edu/jsolomon/assets/MeshBilateral.pdf

22. CARAFE: Content-Aware ReAssembly of FEatures https://arxiv.org/abs/1905.02188

23. Expectation Maximization Attention Networks for Semantic Segmentation https://xialipku.github.io/publication/expectation-maximization-attention-networks-for-semantic-segmentation/

本文为机器之心专栏，转载请联系原作者获得授权。

✄------------------------------------------------

加入机器之心（全职记者 / 实习生）：hr@jiqizhixin.com

投稿或寻求报道：content@jiqizhixin.com

广告 & 商务合作：bd@jiqizhixin.com