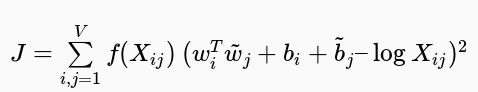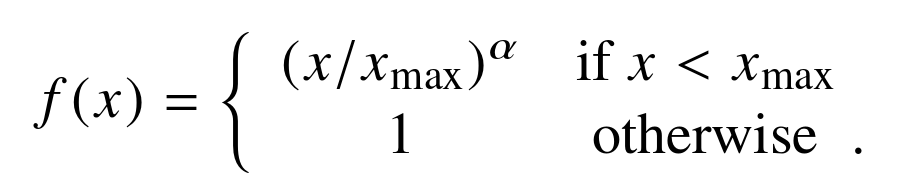Word2Vec与Glove：词嵌入方法的动机和直觉

2018 年 6 月 23 日 论智

作者：weakish

来源：论智

NLP的首要问题就是寻求恰当的文本表示方法。因为，良好的文本表示形式，是后续进一步处理的基础。近年来，词嵌入方法越来越流行，在各种各样的NLP任务中得到了广泛的应用。简单而言，词嵌入是通过无监督方式学习单词的向量表示。本文将首先回顾用向量表示文本的早期模型，并通过分析其缺陷揭示词嵌入提出的动机，然后介绍Word2Vec和Glove这两种最流行的词嵌入方法背后的直觉。

向量空间模型

用向量来表示文本这一想法由来已久。早在1975年，Salton等就提出用向量空间模型来表示文本，以更好地索引、搜索文档。

由于向量空间模型最初的应用场景是索引、搜索，因此更关注词和权重。由词的权重组成向量，并使用这一向量表示整篇文档。

具体而言，假设文档由n个单词组成，那么这篇文档就可以表示为由每个单词的权重组成的n维向量（长度为n的数组），[w₁, w₂, ..., w_n]。当然，为了降低维度，事先会移除一些无关紧要的词（例如the、is）。在实践中，使用一份停止词（stop words）列表移除常见的无关紧要的单词。

权重的计算有很多方法，最常用的是基于词频的方法。具体而言，单词的权重由三个因素决定：

词频（Term Frequency，TF）。词频的计算公式为TF = t / m，其中，t为单词在文档出现的次数，m为文档的长度（总词数）。例如，假设文档由1000个单词组成，其中某个单词总共出现了3次，那么这个单词的词频就等于3/1000.

逆向文档频率 （Inverse Document Frequency，IDF）。IDF衡量单词提供的信息量，换句话说，某个单词是否在所有文档中都很常见/罕见。这背后的直觉很简单。假设100篇文档中，有80篇都包含“手机”这个单词，而只有5篇文档包含“足球”这个单词。那么，对某篇特定文档而言，如果它同时包含“足球”和“手机”这两个单词，这篇文档更可能是一篇关于足球的文档，而不是一篇关于手机的文档，尽管“手机”的词频可能比“足球”高很多。

也就是说，我们需要设法加强“足球”的权重，削弱“手机”的权重。一个很容易想到的办法是用总文档数N除以包含该单词的文档数n，即N/n作为系数。在上面的例子中，“足球”的系数为100/5 = 20，“手机”的系数为100/80 = 1.25.

不过，这里有一个问题，20和1.25是比较大的数字，而词频的取值范围小于1，两者之间的数量级差异太大了。说不定有一篇文档主要是关于手机的，频繁提到“手机”，只提到过一次“足球”，也因为系数数量级的差距导致被误判为关于“足球”的文档。在实践中，文档的总数可能非常大，远不止100，上述缺陷就更严重了。因此，我们需要“压缩”一下，比如取个对数：log(N/n)。我们看到，取对数后，“足球”的系数为log(20) = 2.996，“手机”的系数为log(1.25) = 0.223，好多了。

但是，取了对数之后，当文档总数很多，同时某个单词在几乎所有文档中出现的时候，N/n趋向于1，由对数定义可知，log(N/n)趋向于0. 为了应对这个问题，我们可以在取对数前额外加1平滑下。所以，最终IDF的计算公式为：

  
  
    
   
   
     IDF = log(1 + N/n)

长度正则化 上面TF和IDF的计算，我们假定文档长度差距不大。实际上，文档长度也会影响TF和IDF的效果。

虽然，在计算TF的时候，已经除以文档总词数了，也就是已经考虑到文档长度了。然而这并不能完全消除文档长度的影响。让我们先看IDF（没有考虑文档总词数）的情形。

对于IDF而言，长文档包含的单词更多，因此更容易出现各种单词。因此，IDF相等的情况下，经常出现在短文档中的单词，信息量比经常出现在长文档中的单词要高。例如，假设100篇文档中，有2篇提到了“手机”，有2篇提到了“平板”，那么这两个单词的IDF值均为log(1 + 100/2) = 3.932。然而，假设提到“手机”的两篇文档各自长度为10个单词（一句话），而提到“平板”的两篇文档各自长度为10000个单词（长篇大论）。那么，很明显，IDF相等的“手机”和“平板”，信息量是不同的。在一句话中提到“手机”，那么这句话和手机高度相关的可能性，要比在长篇大论中偶尔提到“平板”大很多。

IDF之后，再回过头来看TF，就比较清楚了。计算IDF时，需要考虑有多少文档出现过某个单词。那么，反过来说，剩下的文档没出现过这个单词，也就是说，该单词在那些剩下的文档中的TF为零。根据之前对IDF的分析，我们知道，同样是TF为零，长文档TF为零和短文档TF为零，意义是不一样的。从另一方面来说，长度为10单词的文档没有提到“平板”，长度为10000单词的文档提到两次“平板”，未必意味着后者就更可能和平板相关。很可能后者只是一篇偶尔提及平板，主要内容和平板完全无关的文档。

1975年Salton等提出基于文档的向量空间模型，原本是为了优化文档的索引和获取。当得到基于文档的向量表示后，可以计算所有文档在整个向量空间中的密度。文档越密集、越扎堆，想要通过特定关键词检索，获取某篇特定文档就更困难。相反，文档在向量空间中，彼此的距离越远，索引系统的效果就越好。然而，这一方法的应用显然并不局限于此。

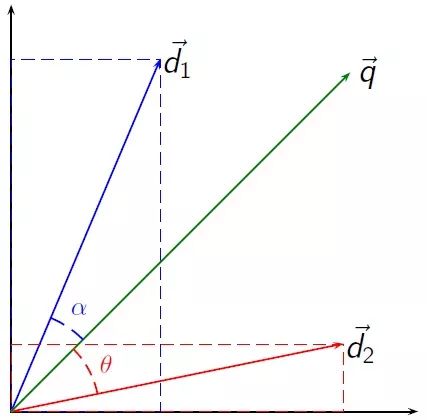
例如，我们可以通过计算文档向量的接近程度（例如，使用余弦相似度）来衡量两个文档的相似度。之后，相似度可以用于文本分类、推荐相似文本等任务。

图片来源：Riclas；许可： CC-BY 3.0

词向量空间

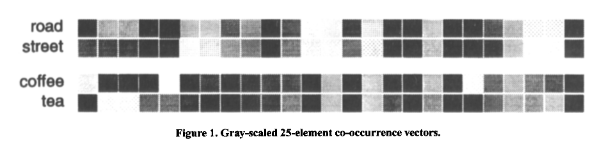
前面我们介绍了基于文档的向量空间模型，这一模型主要是基于频率（词频和逆向文档频率）构建。类似地，基于和其他单词同时出现的频率，我们可以构建基于单词的向量空间模型。词向量空间模型的主要思路是出现在类似的上下文环境中的单词在语义上很可能相似。例如，假如我们发现，“咖啡”和“喝”经常同时出现，另一方面，“茶”和“喝”也经常同时出现，那么我们可以推测“咖啡”和“茶”在语义上应该是相似的。

例如，上图可视化了“路”（road）、“街”（street）以及“咖啡”（coffee）、“茶”（tea）这两对词向量。每个词向量有25个维度（25个上下文中出现的单词），灰度表示同时出现的频率。从图中很明显能看到“路”、“街”的相似性以及“咖啡”、“茶”的相似性。另外，我们也看到，“街”和“咖啡”并不相似。（图片来源于Lund等1996年发表的论文，因年代较早，印刷、扫描的质量不高，图片有点模糊，见谅。）

上面的可视化中，为了便于查看，每个词向量仅有25个维度。实际上，词向量的维度对应于整个语料库的词汇量，因此通常维度高达上万，甚至百万。处理这样的高维向量无疑是一项巨大的挑战。这也正是词向量空间模型的主要缺陷。

为了降低词向量的维度，我们需要词嵌入（Word Embedding）。

词嵌入

词嵌入背后的直觉很简单，既然同时出现的单词在语义上有联系，那么我们可以用某个模型来学习这些联系，然后用这个模型来表示单词。

当前最流行的词嵌入方法是Word2Vec和Glove。下面我们简单介绍下这两种词嵌入方法的主要思路。

Word2Vec

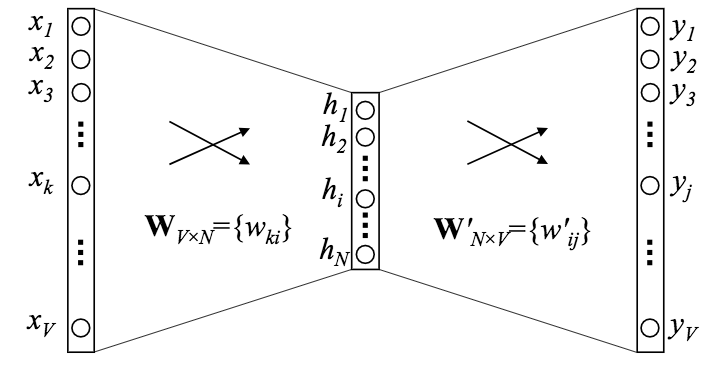
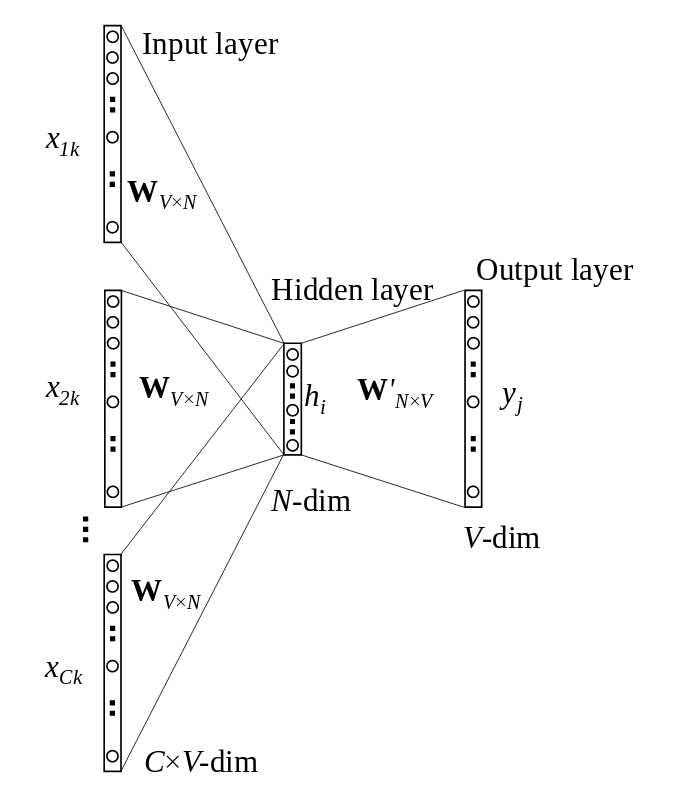
Word2Vec的网络结构很简单，包括一个输入层、一个隐藏层、一个输出层。其中，输入层对应某个（上下文）单词的独热编码向量（共有V个词汇），输出层为与输入单词同时出现的单词的概率分布，换句话说，词汇表中的每个单词，出现在这一上下文中的概率分别是多少。隐藏层由N个神经元组成。

图片来源：Xin Rong arXiv:1411.2738v4

经过训练之后，我们使用输入层和隐藏层之间的连接权重矩阵W_VxN表示单词之间的关系。矩阵W共有V行，每一行都是一个N维向量，每个N维向量分别对应一个单词。这样，词向量的维度就从V降到了N。

我们之前介绍Word2Vec的架构的时候没有提及激活函数。现在我们回过头来补充一下。由于输出层需要输出给定上下文中出现单词的概率分布，因此顺理成章地使用softmax。而Word2Vec的隐藏层不使用激活函数，这看起来有些离经叛道，其实在这一场景中很合适。因为最终我们只需要权重矩阵，并不使用隐藏层的激活函数。因此，为了简化网络架构，Word2Vec的隐藏层不使用激活函数。当然，最后的输出层也没用到，不过隐藏层和输出层之间的权重，以及softmax可不能去掉，否则网络就无法训练了。

当然，上面的网络架构其实是简化过了的。通常，上下文不止一个单词。所以，实际上Word2Vec的网络架构要比上面稍微复杂一点。

图片来源：Xin Rong arXiv:1411.2738v4

和上面简化过的架构相比，唯一的区别是现在有多个上下文单词了。所以，输入不再是某个单词的独热编码向量了，而是多个上下文单词的平均向量。相应地，原本我们仅仅使用输入层和隐藏层之间的权重矩阵来表示单词，现在则使用该权重矩阵和平均向量的乘积。

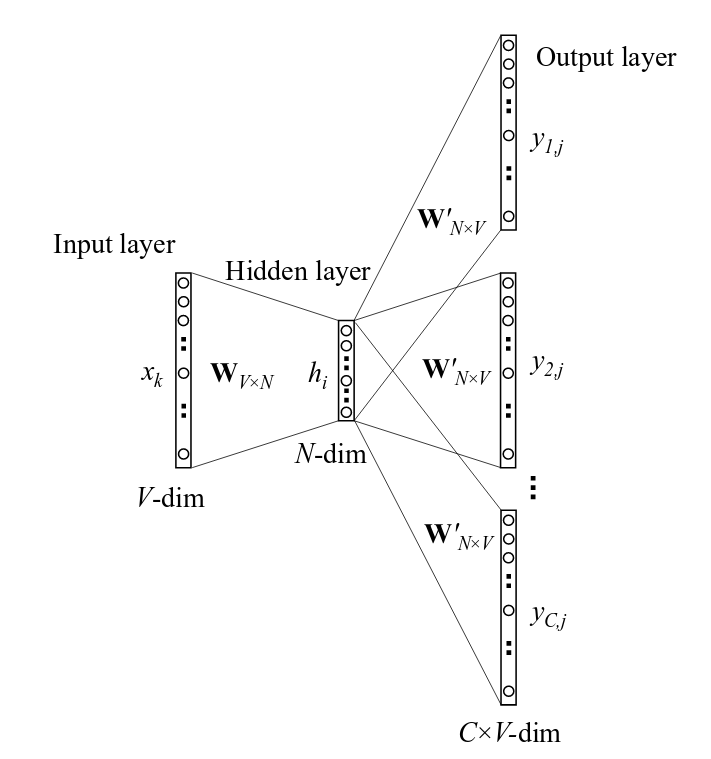
另外，其实我们也可以把上述的网络架构翻转过来，也就是将目标单词作为输入，可能的上下文作为输出。

这两种架构都属于Word2Vec，前者称为CBOW模型，后者称为Skip-Gram模型。

Glove

另一个流行的词嵌入方法是Glove。

之前我们提到，Word2Vec的输出是单词同时出现的概率分布。而Glove的主要直觉是，相比单词同时出现的概率，单词同时出现的概率的比率能够更好地区分单词。比如，假设我们要表示“冰”和“蒸汽”这两个单词。对于和“冰”相关，和“蒸汽”无关的单词，比如“固体”，我们可以期望P_冰-固体/P_{蒸汽-固体}较大。类似地，对于和“冰”无关，和“蒸汽”相关的单词，比如“气体”，我们可以期望P_冰-气体/P_{蒸汽-气体}较小。相反，对于像“水”之类同时和“冰”、“蒸汽”相关的单词，以及“时尚”之类同时和“冰”、“蒸汽”无关的单词，我们可以期望P_冰-水/P_蒸汽-水、P_冰-时尚/P_{蒸汽-时尚}应当接近于1。

另一方面，之前我们已经提到过，Word2Vec中隐藏层没有使用激活函数，这就意味着，隐藏层学习的其实是线性关系。既然如此，那么，是否有可能使用比神经网络更简单的模型呢？

基于以上两点想法，Glove提出了一个加权最小二乘回归模型，输入为单词-上下文同时出现频次矩阵：