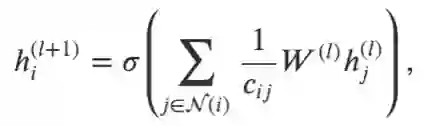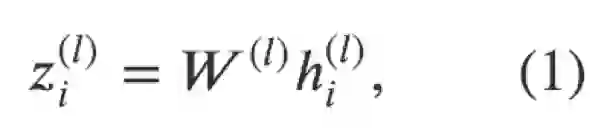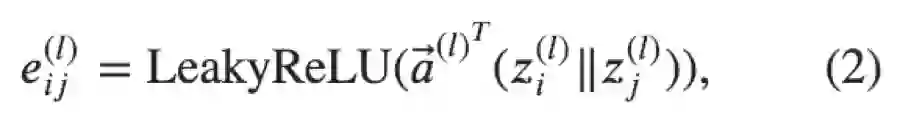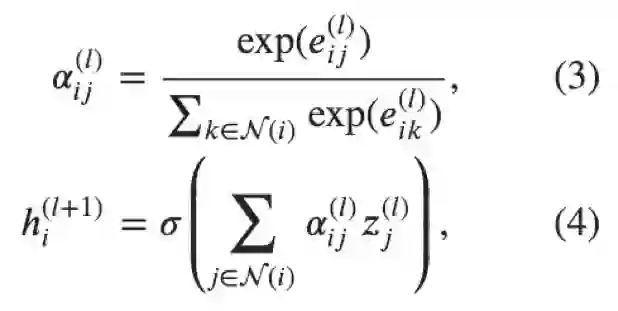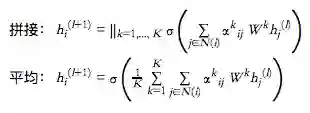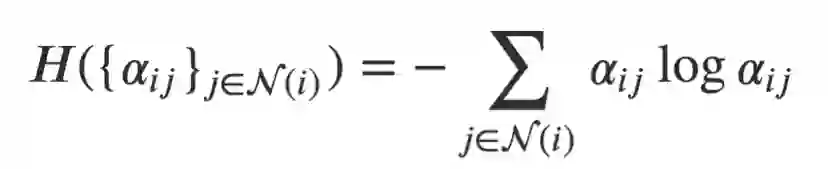专栏 | 深入理解图注意力机制

2019 年 2 月 19 日 机器之心

机器之心DGL专栏

作者：张昊、李牧非、王敏捷、张峥

图卷积网络 Graph Convolutional Network (GCN) 告诉我们将局部的图结构和节点特征结合可以在节点分类任务中获得不错的表现。美中不足的是 GCN 结合邻近节点特征的方式和图的结构依依相关，这局限了训练所得模型在其他图结构上的泛化能力。

Graph Attention Network (GAT) 提出了用注意力机制对邻近节点特征加权求和。邻近节点特征的权重完全取决于节点特征，独立于图结构。

在这个教程里我们将：

解释什么是 Graph Attention Network
演示用 DGL 实现这一模型
深入理解学习所得的注意力权重
初探归纳学习 (inductive learning)

难度：★★★★✩（需要对图神经网络训练和 Pytorch 有基本了解）

在 GCN 里引入注意力机制

GAT 和 GCN 的核心区别在于如何收集并累和距离为 1 的邻居节点的特征表示。

在 GCN 里，一次图卷积操作包含对邻节点特征的标准化求和：

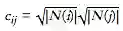
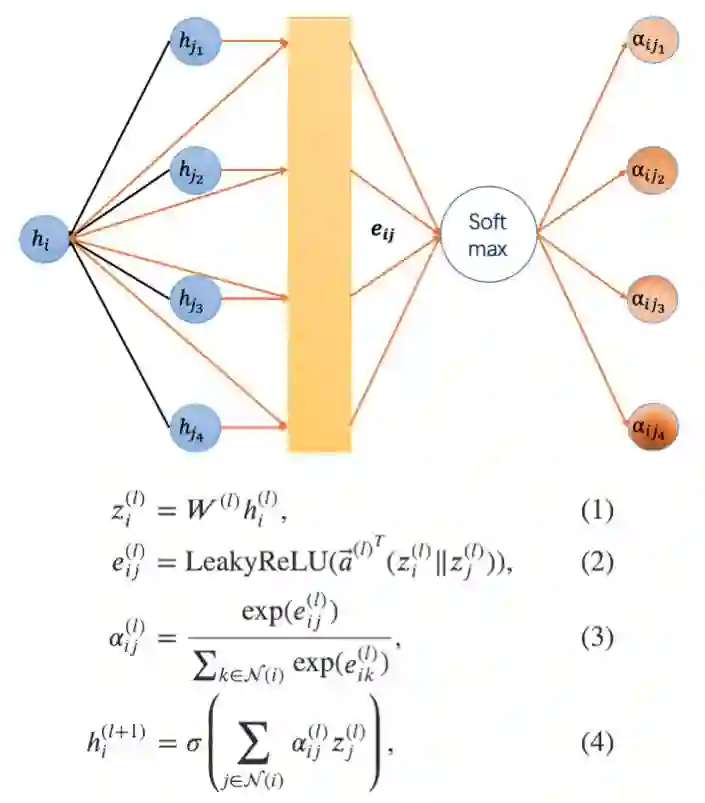
其中 N(i) 是对节点 i 距离为 1 邻节点的集合。我们通常会加一条连接节点 i 和它自身的边使得 i 本身也被包括在 N(i) 里。是一个基于图结构的标准化常数；σ是一个激活函数（GCN 使用了 ReLU）；W^((l)) 是节点特征转换的权重矩阵，被所有节点共享。由于 c_ij 和图的机构相关，使得在一张图上学习到的 GCN 模型比较难直接应用到另一张图上。解决这一问题的方法有很多，比如 GraphSAGE 提出了一种采用相同节点特征更新规则的模型，唯一的区别是他们将 c_ij 设为了|N(i)|。

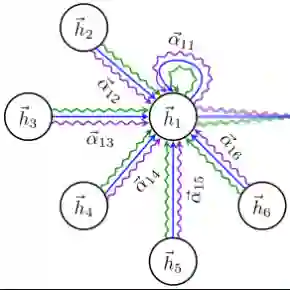
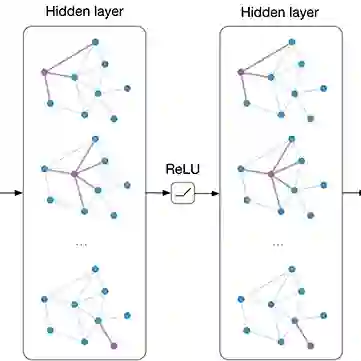
图注意力模型 GAT 用注意力机制替代了图卷积中固定的标准化操作。以下图和公式定义了如何对第 l 层节点特征做更新得到第 l+1 层节点特征：

图 1：图注意力网络示意图和更新公式。

对于上述公式的一些解释：

公式（1）对 l 层节点嵌入做了线性变换，W^((l)) 是该变换可训练的参数
公式（2）计算了成对节点间的原始注意力分数。它首先拼接了两个节点的 z 嵌入，注意 || 在这里表示拼接；随后对拼接好的嵌入以及一个可学习的权重向量做点积；最后应用了一个 LeakyReLU 激活函数。这一形式的注意力机制通常被称为加性注意力，区别于 Transformer 里的点积注意力。
公式（3）对于一个节点所有入边得到的原始注意力分数应用了一个 softmax 操作，得到了注意力权重。
公式（4）形似 GCN 的节点特征更新规则，对所有邻节点的特征做了基于注意力的加权求和。

出于简洁的考量，在本教程中，我们选择省略了一些论文中的细节，如 dropout, skip connection 等等。感兴趣的读者们欢迎参阅文末链接的模型完整实现。

本质上，GAT 只是将原本的标准化常数替换为使用注意力权重的邻居节点特征聚合函数。

GAT 的 DGL 实现

以下代码给读者提供了在 DGL 里实现一个 GAT 层的总体印象。别担心，我们会将以下代码拆分成三块，并逐块讲解每块代码是如何实现上面的一条公式。

import torch
import torch.nn as nn
import torch.nn.functional as F

class GATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim):
        super(GATLayer, self).__init__()
        self.g = g
        # 公式 (1)
        self.fc = nn.Linear(in_dim, out_dim, bias=False)
        # 公式 (2)
        self.attn_fc = nn.Linear(2 * out_dim, 1, bias=False)

    def edge_attention(self, edges):
        # 公式 (2) 所需，边上的用户定义函数
        z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1)
        a = self.attn_fc(z2)
        return {'e' : F.leaky_relu(a)}

    def message_func(self, edges):
        # 公式 (3), (4)所需，传递消息用的用户定义函数
        return {'z' : edges.src['z'], 'e' : edges.data['e']}

    def reduce_func(self, nodes):
        # 公式 (3), (4)所需, 归约用的用户定义函数
        # 公式 (3)
        alpha = F.softmax(nodes.mailbox['e'], dim=1)
        # 公式 (4)
        h = torch.sum(alpha * nodes.mailbox['z'], dim=1)
        return {'h' : h}

    def forward(self, h):
        # 公式 (1)
        z = self.fc(h)
        self.g.ndata['z'] = z
        # 公式 (2)
        self.g.apply_edges(self.edge_attention)
        # 公式 (3) & (4)
        self.g.update_all(self.message_func, self.reduce_func)
        return self.g.ndata.pop('h')

实现公式 (1)

第一个公式相对比较简单。线性变换非常常见。在 PyTorch 里，我们可以通过 torch.nn.Linear 很方便地实现。

实现公式 (2)

原始注意力权重 e_ij 是基于一对邻近节点 i 和 j 的表示计算得到。我们可以把注意力权重 e_ij 看成在 i->j 这条边的数据。因此，在 DGL 里，我们可以使用 g.apply_edges 这一 API 来调用边上的操作，用一个边上的用户定义函数来指定具体操作的内容。我们在用户定义函数里实现了公式（2）的操作：

 def edge_attention(self, edges):
        # 公式 (2) 所需，边上的用户定义函数
        z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1)
        a = self.attn_fc(z2)
        return {'e' : F.leaky_relu(a)}

公式中的点积同样借由 PyTorch 的一个线性变换 attn_fc 实现。注意 apply_edges 会把所有边上的数据打包为一个张量，这使得拼接和点积可以并行完成。

实现公式 (3) 和 (4)

类似 GCN，在 DGL 里我们使用 update_all API 来触发所有节点上的消息传递函数。update_all 接收两个用户自定义函数作为参数。message_function 发送了两种张量作为消息：消息原节点的 z 表示以及每条边上的原始注意力权重。reduce_function 随后进行了两项操作：

使用 softmax 归一化注意力权重（公式（3））。
使用注意力权重聚合邻节点特征（公式（4））。

这两项操作都先从节点的 mailbox 获取了数据，随后在数据的第二维（dim = 1 ) 上进行了运算。注意数据的第一维代表了节点的数量，第二维代表了每个节点收到消息的数量。

 def reduce_func(self, nodes):
        # 公式 (3), (4)所需, 归约用的用户定义函数
        # 公式 (3)
        alpha = F.softmax(nodes.mailbox['e'], dim=1)
        # 公式 (4)
        h = torch.sum(alpha * nodes.mailbox['z'], dim=1)
        return {'h' : h}

多头注意力 (Multi-head attention)

神似卷积神经网络里的多通道，GAT 引入了多头注意力来丰富模型的能力和稳定训练的过程。每一个注意力的头都有它自己的参数。如何整合多个注意力机制的输出结果一般有两种方式：

以上式子中 K 是注意力头的数量。作者们建议对中间层使用拼接对最后一层使用求平均。

我们之前有定义单头注意力的 GAT 层，它可作为多头注意力 GAT 层的组建单元：

class MultiHeadGATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim, num_heads, merge='cat'):
        super(MultiHeadGATLayer, self).__init__()
        self.heads = nn.ModuleList()
        for i in range(num_heads):
            self.heads.append(GATLayer(g, in_dim, out_dim))
        self.merge = merge

    def forward(self, h):
        head_outs = [attn_head(h) for attn_head in self.heads]
        if self.merge == 'cat':
            # 对输出特征维度（第1维）做拼接
            return torch.cat(head_outs, dim=1)
        else:
            # 用求平均整合多头结果
            return torch.mean(torch.stack(head_outs))

在 Cora 数据集上训练一个 GAT 模型

Cora 是经典的文章引用网络数据集。Cora 图上的每个节点是一篇文章，边代表文章和文章间的引用关系。每个节点的初始特征是文章的词袋（Bag of words）表示。其目标是根据引用关系预测文章的类别（比如机器学习还是遗传算法）。在这里，我们定义一个两层的 GAT 模型：

class GAT(nn.Module):
    def __init__(self, g, in_dim, hidden_dim, out_dim, num_heads):
        super(GAT, self).__init__()
        self.layer1 = MultiHeadGATLayer(g, in_dim, hidden_dim, num_heads)
        # 注意输入的维度是 hidden_dim * num_heads 因为多头的结果都被拼接在了
        # 一起。 此外输出层只有一个头。
        self.layer2 = MultiHeadGATLayer(g, hidden_dim * num_heads, out_dim, 1)

    def forward(self, h):
        h = self.layer1(h)
        h = F.elu(h)
        h = self.layer2(h)
        return h

我们使用 DGL 自带的数据模块加载 Cora 数据集。

from dgl import DGLGraph
from dgl.data import citation_graph as citegrh

def load_cora_data():
    data = citegrh.load_cora()
    features = torch.FloatTensor(data.features)
    labels = torch.LongTensor(data.labels)
    mask = torch.ByteTensor(data.train_mask)
    g = DGLGraph(data.graph)
    return g, features, labels, mask

模型训练的流程和 GCN 教程里的一样。

import time
import numpy as np
g, features, labels, mask = load_cora_data()

# 创建模型
net = GAT(g, 
          in_dim=features.size()[1], 
          hidden_dim=8, 
          out_dim=7, 
          num_heads=8)
print(net)

# 创建优化器
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)

# 主流程
dur = []
for epoch in range(30):
    if epoch >=3:
        t0 = time.time()

    logits = net(features)
    logp = F.log_softmax(logits, 1)
    loss = F.nll_loss(logp[mask], labels[mask])

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch >=3:
        dur.append(time.time() - t0)

    print("Epoch {:05d} | Loss {:.4f} | Time(s) {:.4f}".format(
            epoch, loss.item(), np.mean(dur)))

可视化并理解学到的注意力

Cora 数据集

以下表格总结了 GAT 论文以及 dgl 实现的模型在 Cora 数据集上的表现：

可以看到 DGL 能完全复现原论文中的实验结果。对比图卷积网络 GCN，GAT 在 Cora 上有 2~3 个百分点的提升。

不过，我们的模型究竟学到了怎样的注意力机制呢？

由于注意力权重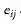与图上的边密切相关，我们可以通过给边着色来可视化注意力权重。以下图片中我们选取了 Cora 的一个子图并且在图上画出了 GAT 模型最后一层的注意力权重。我们根据图上节点的标签对节点进行了着色，根据注意力权重的大小对边进行了着色（可参考图右侧的色条）。

图 2：Cora 数据集上学习到的注意力权重。

乍看之下模型似乎学到了不同的注意力权重。为了对注意力机制有一个全局观念，我们衡量了注意力分布的熵。对于节点 i，{α_ij }_(j∈N(i)) 构成了一个在 i 邻节点上的离散概率分布。它的熵被定义为：

直观地说，熵低代表了概率高度集中，反之亦然。熵为 0 则所有的注意力都被放在一个点上。均匀分布具有最高的熵（log N(i)）。在理想情况下，我们想要模型习得一个熵较低的分布（即某一、两个节点比其它节点重要的多）。注意由于节点的入度不同，它们注意力权重的分布所能达到的最大熵也会不同。

基于图中所有节点的熵，我们画了所有头注意力的直方图。

图 3：Cora 数据集上学到的注意力权重直方图。

作为参考，下图是在所有节点的注意力权重都是均匀分布的情况下得到的直方图。

出人意料的，模型学到的节点注意力权重非常接近均匀分布（换言之，所有的邻节点都获得了同等重视）。这在一定程度上解释了为什么在 Cora 上 GAT 的表现和 GCN 非常接近（在上面表格里我们可以看到两者的差距平均下来不到 2%）。由于没有显著区分节点，注意力并没有那么重要。

这是否说明了注意力机制没什么用？不！在接下来的数据集上我们观察到了完全不同的现象。

蛋白质交互网络 (PPI)

PPI（蛋白质间相互作用）数据集包含了 24 张图，对应了不同的人体组织。节点最多可以有 121 种标签（比如蛋白质的一些性质、所处位置等）。因此节点标签被表示为有 121 个元素的二元张量。数据集的任务是预测节点标签。

我们使用了 20 张图进行训练，2 张图进行验证，2 张图进行测试。平均下来每张图有 2372 个节点。每个节点有 50 个特征，包含定位基因集合、特征基因集合以及免疫特征。至关重要的是，测试用图在训练过程中对模型完全不可见。这一设定被称为归纳学习。

我们比较了 dgl 实现的 GAT 和 GCN 在 10 次随机训练中的表现。模型的超参数在验证集上进行了优化。在实验中我们使用了 micro f1 score 来衡量模型的表现。

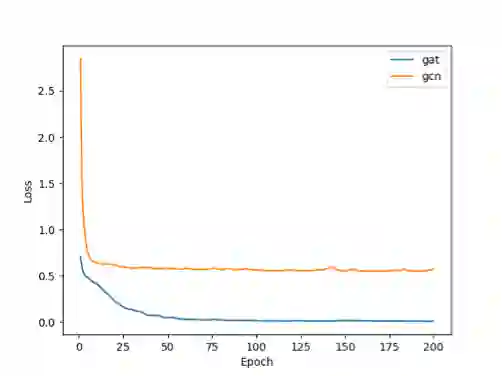
在训练过程中，我们使用了 BCEWithLogitsLoss 作为损失函数。下图绘制了 GAT 和 GCN 的学习曲线；显然 GAT 的表现远优于 GCN。

图 4：PPI 数据集上 GCN 和 GAT 学习曲线比较。

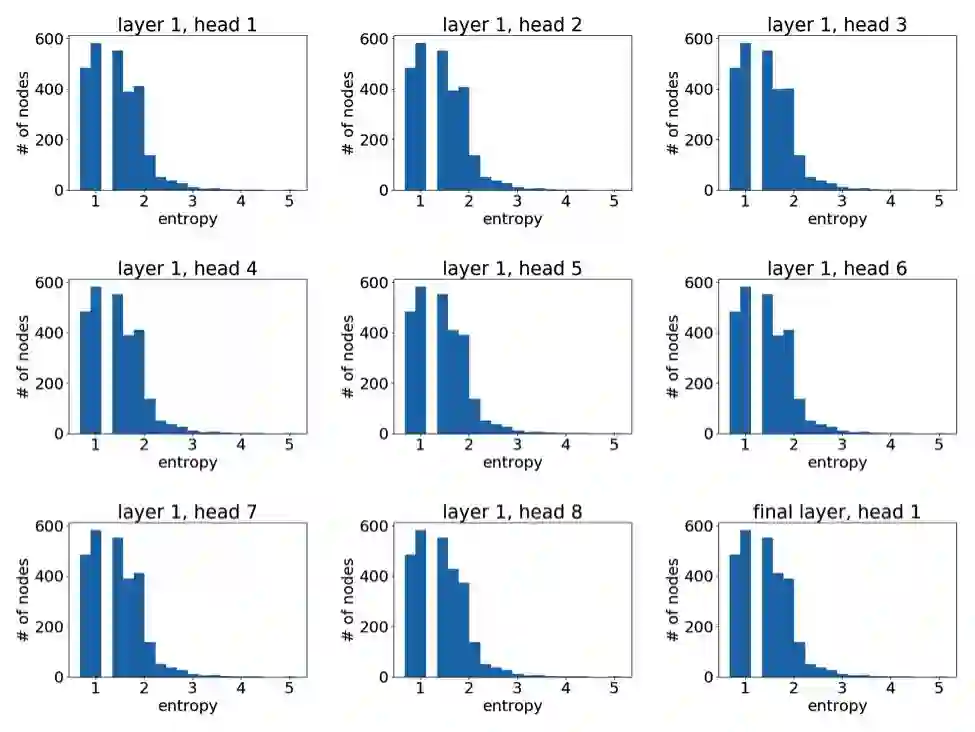
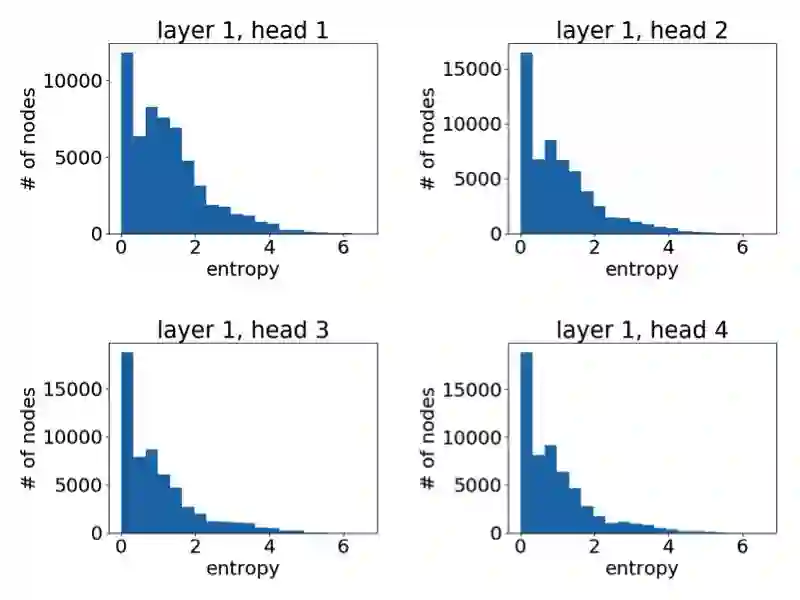
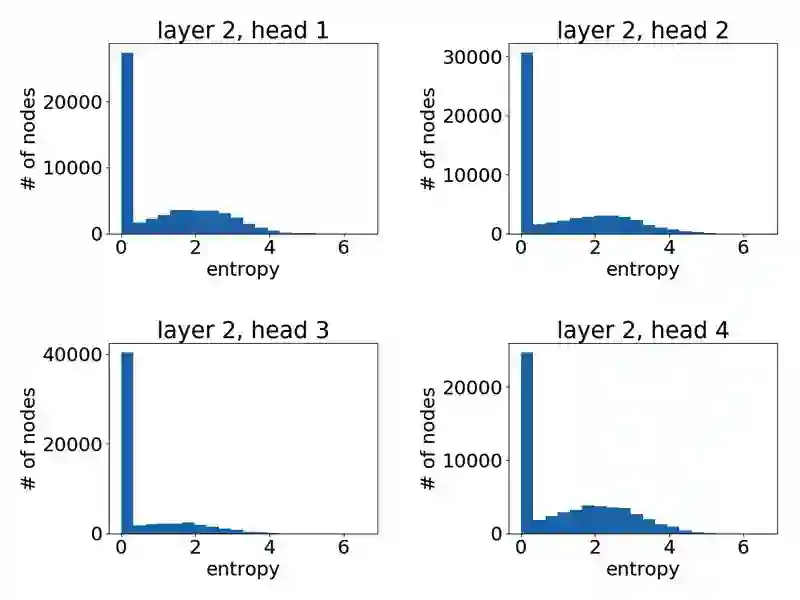
像之前一样，我们可以通过绘制节点注意力分布之熵的直方图来有一个统计意义上的直观了解。以下我们基于一个 3 层 GAT 模型中不同模型层不同注意力头绘制了直方图。

第一层学到的注意力

第二层学到的注意力

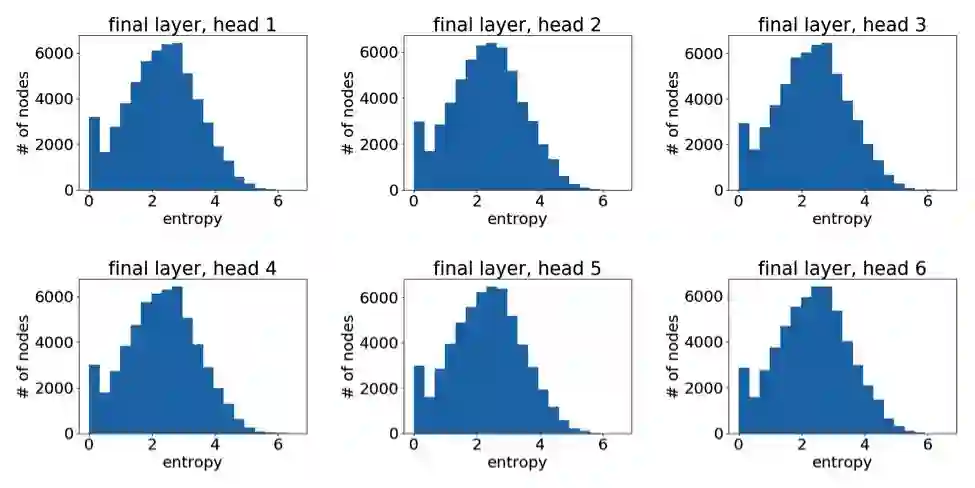
最后一层学到的注意力

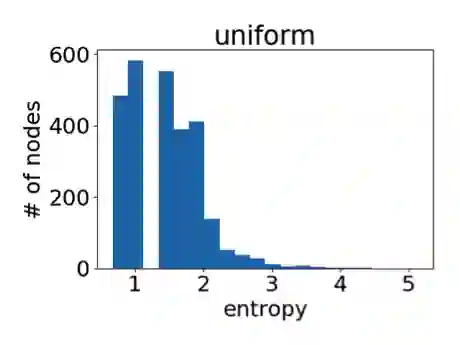
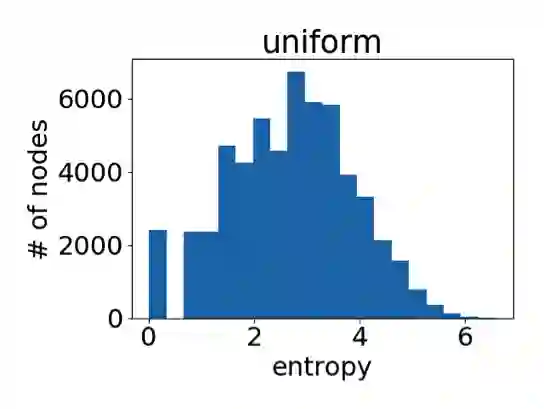
作为参考，下图是在所有节点的注意力权重都是均匀分布的情况下得到的直方图。

可以很明显地看到，GAT 在 PPI 上确实学到了一个尖锐的注意力权重分布。与此同时，GAT 层与层之间的注意力也呈现出一个清晰的模式：在中间层随着层数的增加注意力权重变得愈发集中；最后的输出层由于我们对不同头结果做了平均，注意力分布再次趋近均匀分布。

不同于在 Cora 数据集上非常有限的收益，GAT 在 PPI 数据集上较 GCN 和其它图模型的变种取得了明显的优势（根据原论文的结果在测试集上的表现提升了至少 20%）。我们的实验揭示了 GAT 学到的注意力显著区别于均匀分布。虽然这值得进一步的深入研究，一个由此而生的假设是 GAT 的优势在于处理更复杂领域结构的能力。

拓展阅读

到目前为止我们演示了如何用 DGL 实现 GAT。简介起见，我们忽略了 dropout, skip connection 等一些细节。这些细节很常见且独立于 DGL 相关的概念。有兴趣的读者欢迎参阅完整的代码实现。