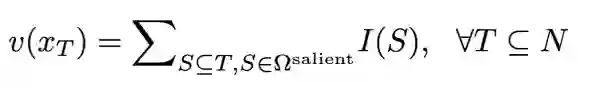该研究发现在大部分情况下,神经网络的表征是清晰的、稀疏的、符号化的。
本文围绕近期的两项工作,讨论神经网络中符号概念的涌现现象,即『
深度神经网络的表征是否是符号化的
』的问题。如果我们绕开 “应用技术提升” 的视角,从 “科学发展” 的角度来重新审视 AI,证明 AI 模型中的符号涌现现象无疑是具有重大意义的。
1. 首先,目前大部分的可解释性研究都在试图将神经网络解释为一个 “清晰的”、“语义化的”、或 “逻辑化的” 模型。但是,如果无法证明神经网络的符号涌现,如果神经网络内在表征成分真的有大量的混乱成分,那么大部分的可解释性研究就失去了其基本事实依据。
2. 其次,如果无法证明神经网络的符号涌现,深度学习的发展将会大概率困在 “结构”、“损失函数”、“数据” 等外围因素的层面,而无法直接高层的认知层面去实现知识层面的交互式学习。往这个方向发展需要更干净清晰的理论支撑。
1. 如何去定义神经网络所建模的符号化概念,从而可靠地发现神经网络的符号涌现现象。
2. 为什么所量化的符号化概念可以认为是可信的概念(稀疏性、对神经网络表征的 universal matching、迁移性、分类性、对历史解释性指标的解释)。
3. 如何证明符号化概念的涌现 —— 即理论证明当 AI 模型在某些情况下(一个并不苛刻的条件),AI 模型的表征逻辑可以解构为极少数的可迁移的符号化概念的分类效用(这部分会在 4 月底公开讨论)。
![]()
论文地址:https://arxiv.org/pdf/2111.06206.pdf
![]()
论文地址:https://arxiv.org/pdf/2302.13080.pdf
该研究作者包括上海交通大学硕士二年级学生李明杰、上海交通大学博士三年级学生任洁,李明杰和任洁都师从张拳石老师。他们所在的实验室团队常年做神经网络可解释性的研究。对于可解释性领域,研究者可以从不同角度来分析,有解释表征的,有解释性能的,有相对可靠合理的,也有不合理的。但是,深入讨论下去,对神经网络的解释有两个根本的愿景,即「
能否清晰且严谨地表示出神经网络所建模的概念」
和
「能否准确解释出决定神经网络性能的因素
」。
在「解释神经网络所建模的概念」这一方向上,所有研究者都必须面对的一个核心问题 ——“
神经网络的表征到底是不是符号化概念化的
”。如果这个问题回答不清楚,那么后续的研究很难进行 —— 如果神经网络的表征本身都是混乱的,然后研究者强行用一堆 “符号化的概念” 或 “因果逻辑” 去解释,这样一来方向就错了?对神经网络符号化表征的假设,是进行深入研究该领域的基础,但是对此问题的论证往往让人无从下手。
大部分研究者对神经网络的第一直觉是 “它不可能是符号化的吧?” 神经网络毕竟不是图模型。在一篇由 Cynthia 等人撰写的论文中《Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead》 [3],,让人们误以为对神经网络的事后解释(post-hoc explanation)天然地是不可靠的。
那么,神经网络内在表征真的是非常混乱的?而不是清晰的、稀疏的、符号化的吗?围绕这个问题,我们定义了博弈交互 [4,5],证明了神经网络表征瓶颈 [6],研究了神经网络对视觉概念表征的特点 [7,8],从而证明了交互概念与神经网络泛化和鲁棒性的关系 [9,10,11,12],进而完善了沙普利值 [13],但是实验室前期仅仅围绕 “符号化表征” 核心的周边进行探索,始终无法直接探索
神经网络表征是否是符号化的
。
这里我们先说结论 ——
在大部分情况下,神经网络的表征是清晰的、稀疏的、符号化的
。这个结论背后有大量的理论证明,以及大量的实验论证。在理论方面,我们目前的研究证明了一些可以支撑 “符号化” 的特性,但是目前证明还不足以对 “符号化表征” 给出严谨明确的解答。未来几个月,我们会有更加严谨、全面的证明。
在分析神经网络之前,我们需要明确 “如何定义网络所建模的概念”。实际上,对于这一问题,之前已经有了相关研究 [14,15],并且实验结果也比较优异 —— 但是,我们认为,“概念” 的定义在理论上应有 “
严谨性
” 的数学保证。
因此,我们在论文 [1] 中定义了 I(S) 这一指标,用来量化概念 S 对于网络输出的效用,这里 S 指的是组成这一概念的所有输入变量的集合。例如,给定一个神经网络
![]() 和一个输入句子 x=“I think he is a green hand.”,每个单词可以看成网络的其中一个输入变量,句中的三个词 “a”,“green”,“hand” 可以构成一个潜在的概念 S={a,green,hand}。每个概念 S 表示了 S 中
输入变量之间的 “与” 关系:
当且仅当 S 中的输入变量全部出现时,这一概念才被触发,从而为网络输出贡献 I (S) 的效用。而当 S 中任意变量被遮挡时,I (S) 这部分效用就从原本的网络输出中移除了。例如,对于 S={a,green,hand} 这一概念,如果把输入句子中的 “hand” 一词遮挡,那么这一概念就不被触发,网络输出中也不会包含这一概念的效用 I (S)。
我们证明了神经网络输出总可以被拆分为所有触发概念效用之和。即在理论上,对于一个包含 n 个输入单元的样本,最多有
和一个输入句子 x=“I think he is a green hand.”,每个单词可以看成网络的其中一个输入变量,句中的三个词 “a”,“green”,“hand” 可以构成一个潜在的概念 S={a,green,hand}。每个概念 S 表示了 S 中
输入变量之间的 “与” 关系:
当且仅当 S 中的输入变量全部出现时,这一概念才被触发,从而为网络输出贡献 I (S) 的效用。而当 S 中任意变量被遮挡时,I (S) 这部分效用就从原本的网络输出中移除了。例如,对于 S={a,green,hand} 这一概念,如果把输入句子中的 “hand” 一词遮挡,那么这一概念就不被触发,网络输出中也不会包含这一概念的效用 I (S)。
我们证明了神经网络输出总可以被拆分为所有触发概念效用之和。即在理论上,对于一个包含 n 个输入单元的样本,最多有
![]() 种不同的遮挡方式,我们总可以用『少量概念』的效用来『精确拟合』神经网络『所有
种不同的遮挡方式,我们总可以用『少量概念』的效用来『精确拟合』神经网络『所有
![]() 种』不同遮挡样本上的输出值,从而证明了 I (S) 的『严谨性』
。下图给了一个简单的例子。
种』不同遮挡样本上的输出值,从而证明了 I (S) 的『严谨性』
。下图给了一个简单的例子。
![]()
![]()
进一步,我们在论文 [1] 中证明了 I (S) 满足博弈论中 7 条性质,进一步说明了这一指标的可靠性。
![]()
除此以外,我们还证明了博弈交互概念 I (S)
能够解释博弈论中大量经典指标的基本机理,比如 Shapley value [16]、Shapley interaction index [17],以及 Shapley-Taylor interaction index [18]。
具体地,我们可以将这三种指标表示为交互概念的不同线性和的形式。
![]()
实际上,课题组的前期工作已经基于博弈交互概念指标来定义 Shapley value 的最优基准值 [13],并探索视觉神经网络所建模的『原型视觉概念』及其『美观度』[8]。
有了这一指标,我们进一步探索上面提到的核心问题:神经网络是否真的能从训练任务中总结出清晰的、符号化的、概念化的表征?所定义的交互概念真的能表示一些有意义的 “知识”,还是仅仅是一个纯粹从数学上凑出来的没有明确意义的 tricky metrics?为此,我们从以下四个方面回答这一问题 —— 符号化概念化的表征应当满足稀疏性、样本间迁移性、网络间迁移性,以及分类性。
要求一(概念稀疏性):神经网络所建模的概念应当是稀疏的
不同于连结主义,符号主义的一个特性在于人们希望用少量的、稀疏的概念来表示网络学到的知识,而不是用大量、稠密的概念。实验中我们发现,在大量潜在概念中,仅有非常少量的显著概念。即大部分交互概念的交互效用 I (S) 趋近于 0,故可以忽略,仅有极少量的交互概念有较显著的交互效用 I (S),这样神经网络的输出仅仅决定于少量概念的交互效用。换句话说,神经网络对于每个样本的推断可以被简洁地解释为少量显著概念的效用。
![]()
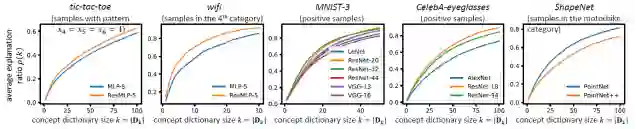
要求二(样本间迁移性):神经网络所建模的概念在不同样本间应当具有迁移性
在单个样本上满足稀疏性是远远不够的,更重要的是,这些稀疏的概念表达应当能够在不同样本之间互相迁移。如果同一个交互概念可以在不同样本中表征,如果不同样本总提取出类似的交互概念,那么这个交互概念更可能代表一种有意义的普适的知识。反之,如果大部分交互概念仅仅在一两个特定样本上有表征,那么这样所定义的交互更倾向于一个仅有数学定义但没有物理意义的 tricky metric。在实验中,我们发现,往往存在一个较小的概念字典,它能够解释神经网络为同类别样本所建模的大部分概念。
![]()
我们也可视化了一些概念,并且发现,相同的概念通常对不同的样本产生类似的效果,这也验证了概念在不同样本之间的迁移性。
![]()
![]()
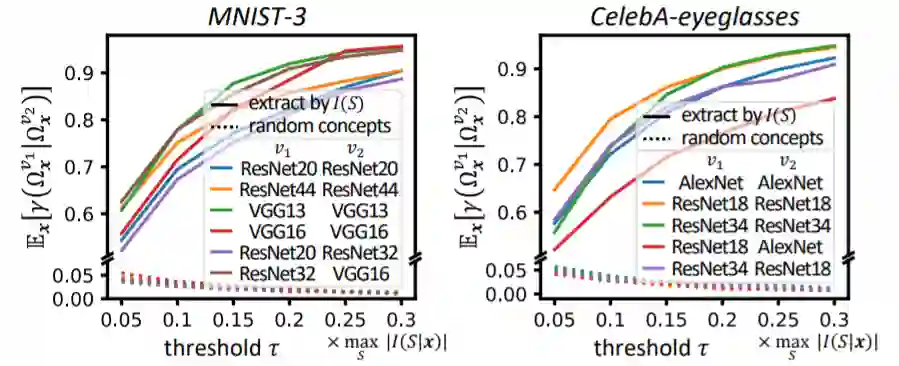
要求三(网络间迁移性):不同神经网络所建模的概念之间应当具有迁移性
类似地,这些概念应当能够被不同的神经网络稳定地学到,无论是不同初始化的网络,还是不同架构的网络。虽然神经网络可以设计为全然不同的架构,建模不同维数的特征,但是如果不同的神经网络面对同一个具体任务可以实现『殊途同归』,即如果不同神经网络都可以稳定地学习到类似的一组交互概念,那么我们可以认为这组交互概念是面向这个任务的根本的表征。比如,如果不同的人脸检测网络都不约而同地建模了眼睛、鼻子、嘴之间的交互,那么我们可以认为这样的交互是更 “本质的”“可靠的”。在实验中,我们发现,越显著的概念越容易被不同的网络同时学到,相对比例的显著交互是被不同神经网络所共同建模的。
![]()
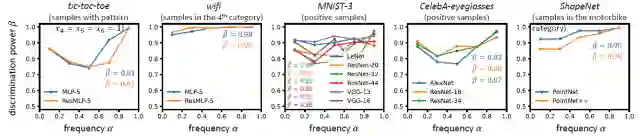
要求四(概念分类性):神经网络所建模的概念应当具有分类性
最后,对于分类任务而言,如果一个概念具有较高的分类性,那么它应当为大多数样本上的分类起到一致的正向作用(或是一致的负向作用)。较高的分类性可以验证这个概念可以独立地承担分类任务,从而更大可能的是一个可靠的概念,而不是不成熟的中间特征。我们同样设计了实验来验证这一性质,发现神经网络建模的概念往往具有较高的分类性。
![]()
综上所述,上面的四个方面表明,在大部分情况下,神经网络的表征是清晰的、稀疏的、符号化的。当然,神经网络也并不是每时每刻都能够建模这种清晰、符号化的概念,在少数极端情况下,神经网络学不到稀疏、可迁移的概念,具体请看我们的论文 [2]。
1. 从可解释性领域发展的角度来看,最直接的意义就是为 “概念层面解释神经网络” 找到了一定的依据。如果神经网络本身的表征都不是符号化的,那么从符号化概念层面对神经网络的解释就只能是隔靴搔痒,解释的结果一定是似是而非的,并不能实质性的推导深度学习进一步的发展。
2. 从 2021 年开始,我们逐步构建了一个基于博弈交互的理论体系。发现基于博弈交互,我们可以统一解释两个核心问题 “怎样量化神经网络所建模的知识” 和 “怎样解释神经网络的表征能力”。在 “怎样量化神经网络所建模的知识” 方向上,除了本文提到的两个工作之外,课题组的前期工作已经基于博弈交互概念指标,来定义 Shapley value 的最优基准值 [13],并探索视觉神经网络所建模的『原型视觉概念』及其『美观度』[7,8]。
3. 在 “怎样解释神经网络的表征能力” 方向上,课题组证明了神经网络对不同交互的表征瓶颈 [6],研究了神经网络如何通过其所建模的交互概念来确定其泛化性 [12,19],研究神经网络所建模的交互概念与其对抗鲁棒性和对抗迁移性的关系 [9,10,11,20],证明了贝叶斯神经网络更难以建模复杂交互概念 [21]。
https://zhuanlan.zhihu.com/p/264871522/
[1] Ren et al. “Can we faithfully represent masking states to compute Shapley values on a DNN?”in CVPR 2023
[2] Li et al. “Does a Neural Network Really Encode Symbolic Concepts?” in arXiv:2302.13080
[3] Rudin, Cynthia. “Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead.” Nature machine intelligence (2019): 206-215. URL: https://www.nature.com/articles/s42256-019-0048-x
[4] Zhang et al. “Interpreting multivariate Shapley interactions in DNNs.” AAAI 2021. Vol. 35. No. 12. 2021. URL: https://arxiv.org/abs/2010.05045 Zhihu blog: https://zhuanlan.zhihu.com/p/264953129
[5] Zhang et al. “Building interpretable interaction trees for deep NLP models.” AAAI 2021. URL: https://arxiv.org/abs/2007.04298. Zhihu blog: https://zhuanlan.zhihu.com/p/264953129
[6] Deng et al. “Discovering and explaining the representation bottleneck of DNNs.” ICLR 2022. URL: https://arxiv.org/abs/2111.06236 Zhihu blog: https://zhuanlan.zhihu.com/p/422420088
[7] Cheng et al. “A game-theoretic taxonomy of visual concepts in dnns.” arXiv:2106.10938 (2021). URL: https://arxiv.org/abs/2106.10938 Zhihu blog: https://zhuanlan.zhihu.com/p/386548661
[8] Cheng et al. “A hypothesis for the aesthetic appreciation in neural networks.” arXiv:2108.02646 (2021). URL: https://arxiv.org/abs/2108.02646 Zhihu blog: https://zhuanlan.zhihu.com/p/395709713
[9] Wang et al. “A unified approach to interpreting and boosting adversarial transferability.” ICLR 2021. URL: https://arxiv.org/abs/2010.04055 Zhihu blog: https://zhuanlan.zhihu.com/p/369883667
[10] Ren et al. “A unified game-theoretic interpretation of adversarial robustness.” NeurIPS 2021. URL: https://arxiv.org/abs/2111.03536 Zhihu blog: https://zhuanlan.zhihu.com/p/361686461
[11] Zhang et al. “Proving Common Mechanisms Shared by Twelve Methods of Boosting Adversarial Transferability.” arXiv:2207.11694 (2022). URL: https://arxiv.org/abs/2207.11694 Zhihu blog: https://zhuanlan.zhihu.com/p/546433296
[12] Zhang et al. “Interpreting and boosting dropout from a game-theoretic view.” ICLR 2021. URL: https://arxiv.org/abs/2009.11729. Zhihu blog: https://zhuanlan.zhihu.com/p/345561960
[13] Ren et al. “Can We Faithfully Represent Masking States to Compute Shapley Values on a DNN?” ICLR 2023. URL: https://arxiv.org/abs/2105.10719 Zhihu blog: https://zhuanlan.zhihu.com/p/395674023
[14] Bau et al. “Network dissection: Quantifying interpretability of deep visual representations.” CVPR 2017. URL: http://openaccess.thecvf.com/content_cvpr_2017/html/Bau_Network_Dissection_Quantifying_CVPR_2017_paper.html
[15] Kim et al. “Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (TCAV).” ICML 2018. URL: http://proceedings.mlr.press/v80/kim18d.html
[16] Shapley, L. S. A value for n-person games. Contributions to the Theory of Games, 2 (28):307–317, 1953.
[17] Grabisch, M. and Roubens, M. An axiomatic approach to the concept of interaction among players in cooperative games. International Journal of game theory, 28 (4):547–565, 1999.
[18] Sundararajan et al. "The Shapley Taylor interaction index." ICML 2020. URL: http://proceedings.mlr.press/v119/sundararajan20a.html
[19] Zhou et al. “Concept-Level Explanation for the Generalization of a DNN” arXiv:2302.13091 (2023), URL: https://arxiv.org/abs/2302.13091
[20] Wang et al. “Interpreting Attributions and Interactions of Adversarial Attacks” ICCV 2021.
[21] Ren et al. “Bayesian Neural Networks Tend to Ignore Complex and Sensitive Concepts”
arXiv:2302.13095 (2023), URL: https://arxiv.org/abs/2302.13095
[22] Shen et al. "Can the Inference Logic of Large Language Models be Disentangled into Symbolic Concepts?"arXiv:2304.01083(2023), URL: https://arxiv.org/abs/2304.01083
![]()
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
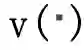 和一个输入句子 x=“I think he is a green hand.”,每个单词可以看成网络的其中一个输入变量,句中的三个词 “a”,“green”,“hand” 可以构成一个潜在的概念 S={a,green,hand}。每个概念 S 表示了 S 中
输入变量之间的 “与” 关系:
当且仅当 S 中的输入变量全部出现时,这一概念才被触发,从而为网络输出贡献 I (S) 的效用。而当 S 中任意变量被遮挡时,I (S) 这部分效用就从原本的网络输出中移除了。例如,对于 S={a,green,hand} 这一概念,如果把输入句子中的 “hand” 一词遮挡,那么这一概念就不被触发,网络输出中也不会包含这一概念的效用 I (S)。
和一个输入句子 x=“I think he is a green hand.”,每个单词可以看成网络的其中一个输入变量,句中的三个词 “a”,“green”,“hand” 可以构成一个潜在的概念 S={a,green,hand}。每个概念 S 表示了 S 中
输入变量之间的 “与” 关系:
当且仅当 S 中的输入变量全部出现时,这一概念才被触发,从而为网络输出贡献 I (S) 的效用。而当 S 中任意变量被遮挡时,I (S) 这部分效用就从原本的网络输出中移除了。例如,对于 S={a,green,hand} 这一概念,如果把输入句子中的 “hand” 一词遮挡,那么这一概念就不被触发,网络输出中也不会包含这一概念的效用 I (S)。
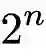 种不同的遮挡方式,我们总可以用『少量概念』的效用来『精确拟合』神经网络『所有
种不同的遮挡方式,我们总可以用『少量概念』的效用来『精确拟合』神经网络『所有
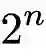 种』不同遮挡样本上的输出值,从而证明了 I (S) 的『严谨性』
。下图给了一个简单的例子。
种』不同遮挡样本上的输出值,从而证明了 I (S) 的『严谨性』
。下图给了一个简单的例子。