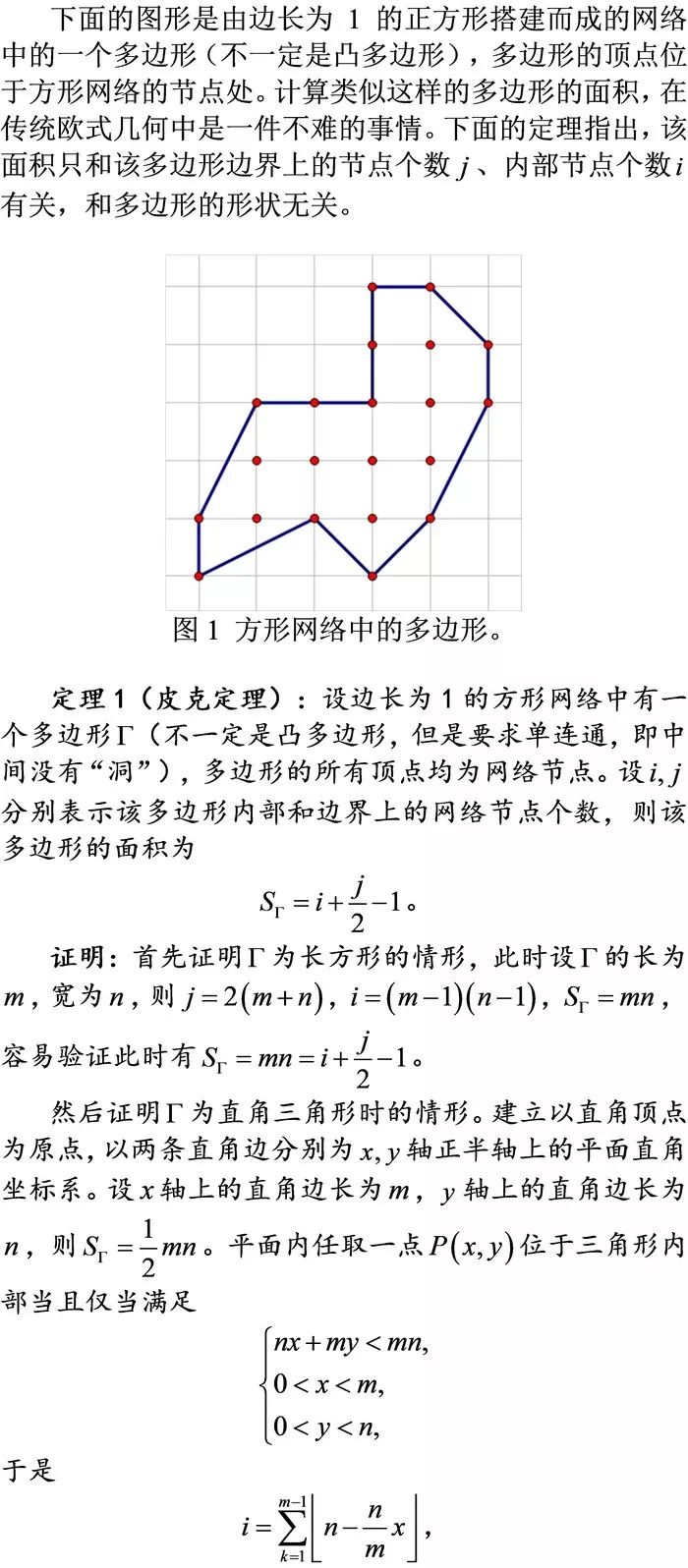
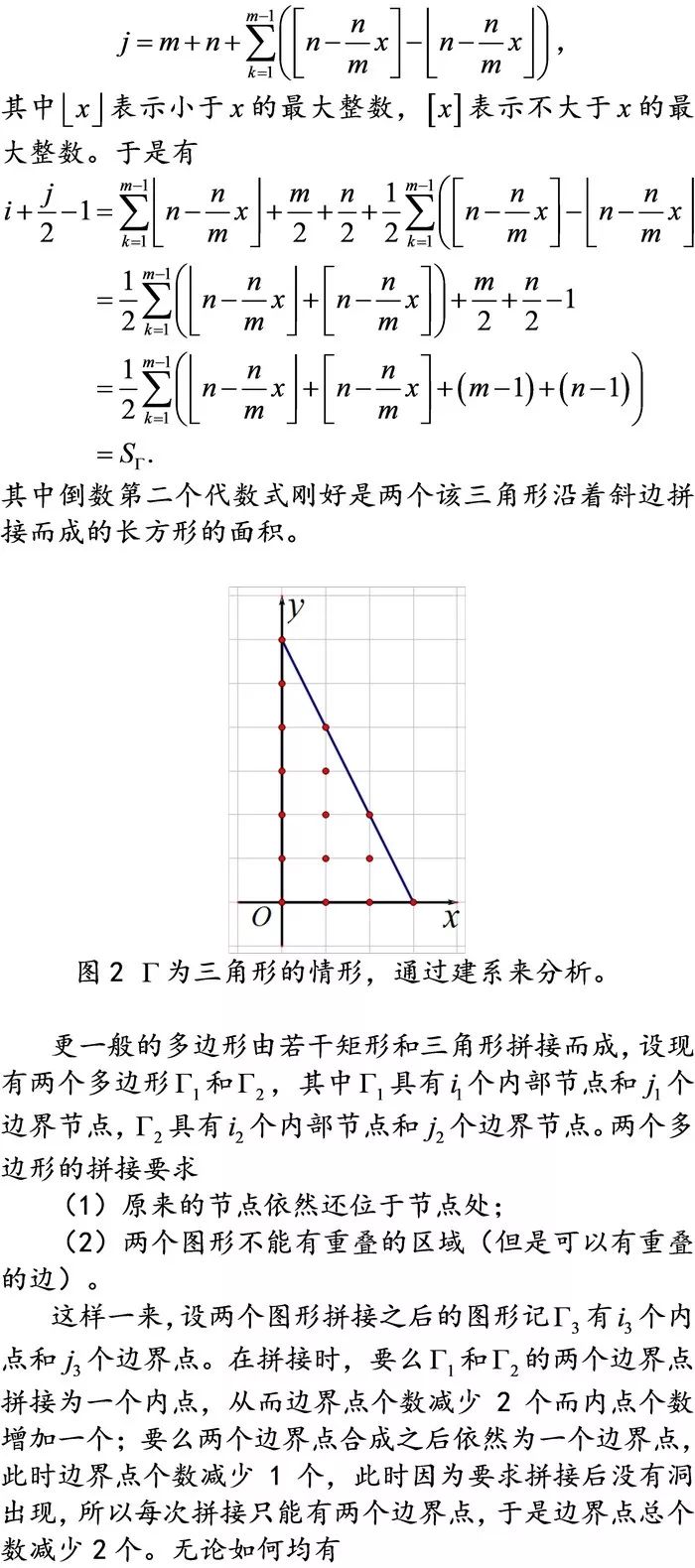
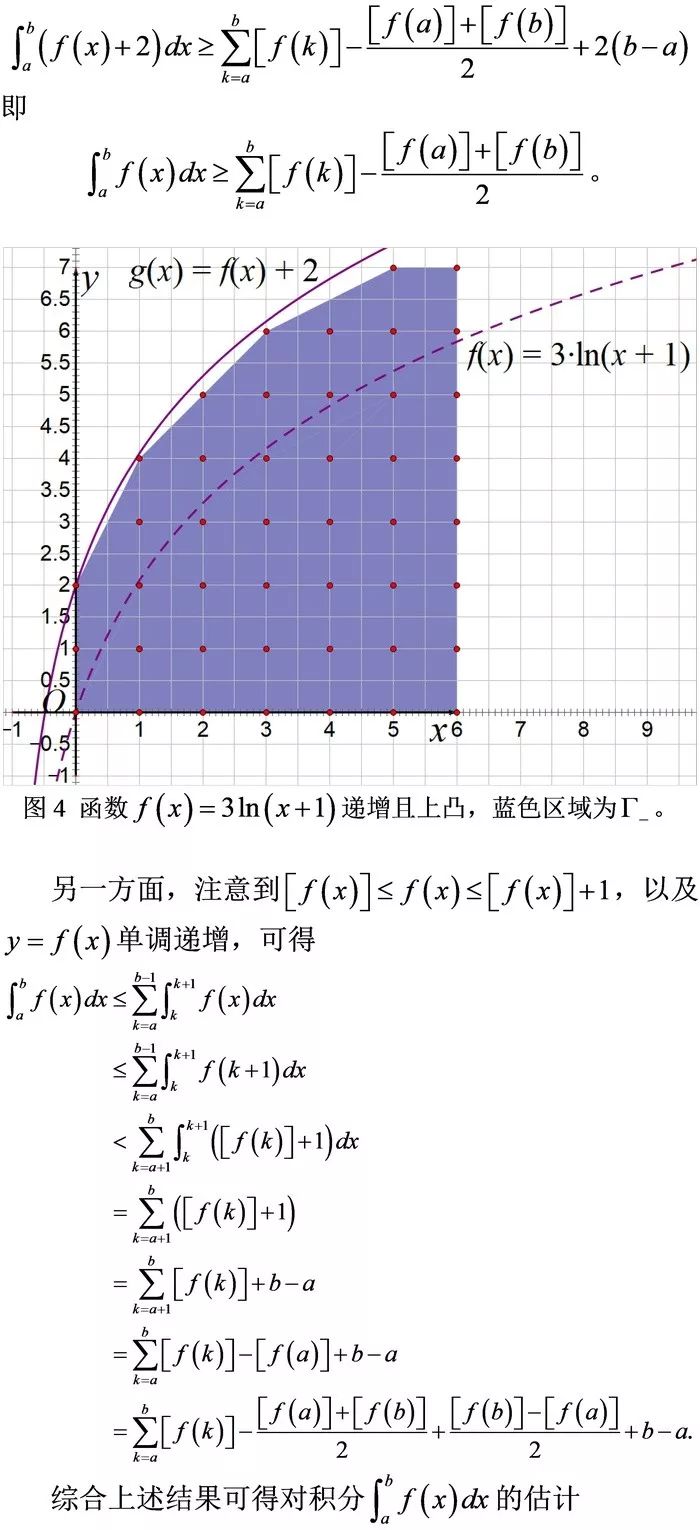
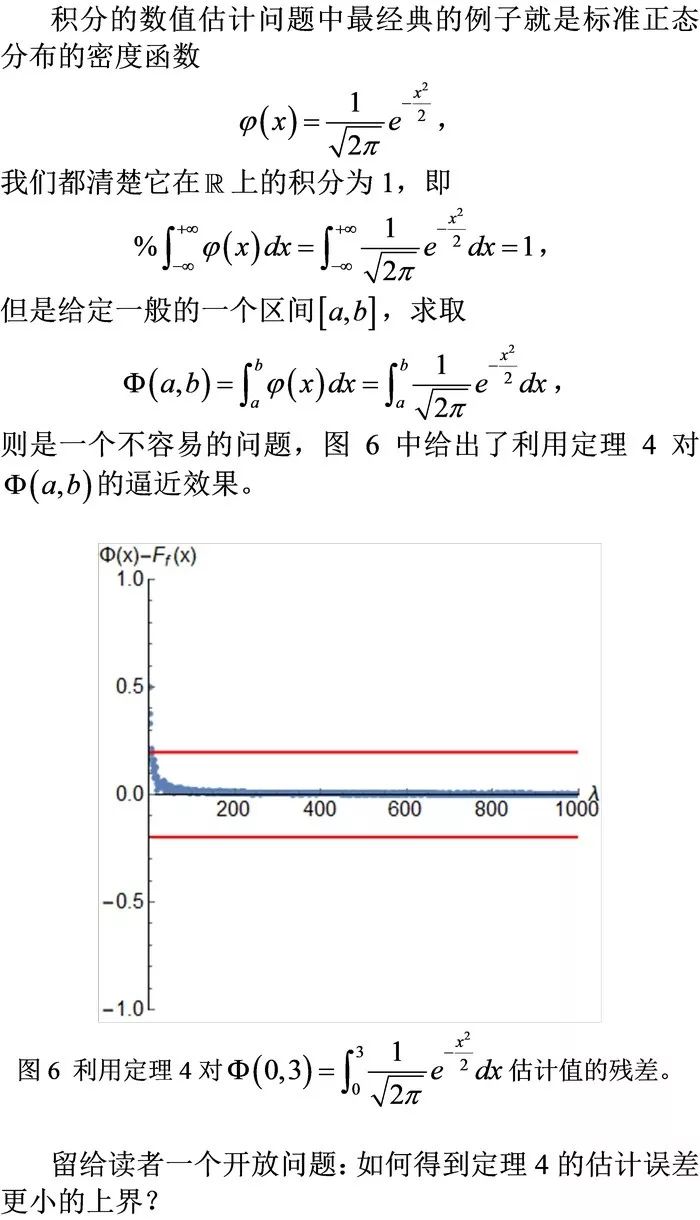
数学建模10：欧式与离散几何的桥梁——皮克定理及其应用

本讲导读

       在信息时代，图像和信息均以数位方式给出，这与连续情形下的传统欧式几何有明显的不同，也为分析带来了障碍。本讲讨论传统欧式几何与近代数位几何之间起到联系作用的皮克定理及其应用。

       本讲适合在讲授或学习完高中数学的数列章节、函数章节、平面解析几何章节、定积分章节后，作为数学建模材料，在日常教学中讲授或学习，本讲内容包括但不限于：

1. 皮克定理及其证明；（配图）

2. 应用1：估算北京市五环内的面积以及数据直径；（配图）

3. 应用2：积分的离散估计定理。（配图）

延申阅读材料：

[1] R.C. Churchill , Liouville’s Theorem onIntegration in Terms of Elementary Functions, Kolchin Seminar on DifferentialAlgebra, 2006.
在线阅读及下载地址：
http://www.sci.ccny.cuny.edu/~ksda/PostedPapers/liouv06.pdf。

日常生活中的数学建模系列文章：

» 日常生活 01: 日常生活中的等差数列和等比数列

» 日常生活 02: 二次和三次函数样条、数据的插值

» 日常生活 03: 指数函数与对数函数的普适价值

» 日常生活 04: 三角函数与极小曲面

» 日常生活 05: 概率的加法与乘法原理、加权平均的递推

» 日常生活 06: 解析几何与带标签数据的模糊线性分类

» 日常生活 07: 进制观点下的分类、距离与解析

» 日常生活 08: 迭代预测的测不准原理与熵距

» 日常生活 09: 数据直径、荣格定理及凸集