【干货】深入理解自编码器（附代码实现）

【导读】自编码器可以认为是一种数据压缩算法，或特征提取算法。本文作者Nathan Hubens 介绍了autoencoders的基本体系结构。首先介绍了编码器和解码器的概念，然后就“自编码器可以做什么？”进行讨论，最后分别讲解了四种不同类型的自编码器：普通自编码器，多层自编码器，卷积自编码器和正则化自编码器。文中给出不同类型的自编码器的GitHub链接，感兴趣的读者不妨仔细研读一下。

 

自编码器PyTorch实现，可以参见：

自编码器, 以及如何用PyTorch实现自编码器

 

Deep inside: Autoencoders

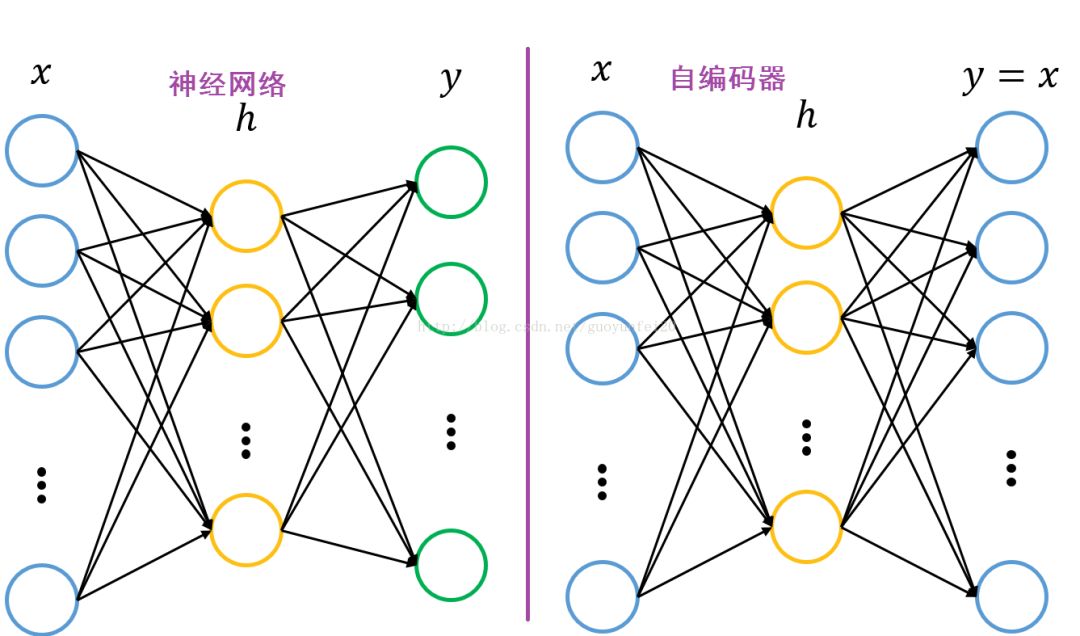
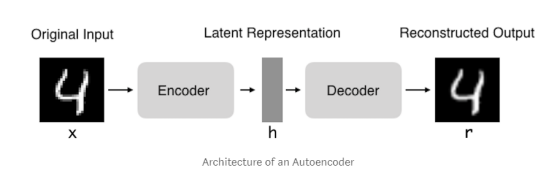
自编码器指的是试图让输出和输入一样的神经网络。他们通过将输入压缩成一个隐藏空间表示来进行工作，然后通过这种表示重构输出。 这种网络由两部分组成：

1.编码器：这是自编码网络的一部分，功能在于把输入变成一个隐藏的空间表示。 它可以用一个编码函数h = f（x）表示。

2.解码器：这部分旨在从隐藏空间的表示重构输入。 它可以用解码函数r = g（h）表示。

作为一个整体的自编码器可以用函数g（f（x））= r来描述，其中r与原始输入x相近。

▌为什么要将输入复制到输出中？

---

---

如果autoencoders的唯一目的是将输入复制到输出中，那么它们将毫无用处。 实际上，我们希望通过训练autoencoder将输入复制到输出中，隐藏表示h将具有有用的属性。

这可以通过在复制任务上添加一些限制条件进行实现。从自编码器获得有用特征的一种方法是将h限制为小于x的维度，在这种情况下，自编码器是不完整的。通过训练不完整的表示，我们强制自编码器学习训练数据的最显著特征。如果自编码器的容量过大，自编码器可以出色地完成赋值任务而没有从数据的分布抽取到任何有用的信息。如果隐藏表示的维度与输入相同，或者隐藏表示维度大于输入维度的情况下，也会发生这种情况。在这些情况下，即使线性编码器和线性解码器也可以将输入复制到输出，而无需了解有关数据分配的任何有用信息。理想情况下，自编码器可以成功地训练任何体系结构，根据要分配的复杂度来选择编码器和解码器的代码维数和容量。

▌自编码器可以用于干什么？

---

---

当前，数据去噪和数据可视化中的降维被认为是自编码器的两个主要的实际应用。通过适当的维度和稀疏性约束，自编码器可以学习比PCA或其他基本技术更有趣的数据投影。

自编码器通过数据样本自动学习。这意味着很容易训练特定的算法实例，该算法在特定类型的输入中表现良好，并且不需要任何新工程，只需要适当的训练数据。

但是，自编码器在图像压缩方面做得不好。 由于自编码器是在给定的一组数据上进行训练的，因此它将对类似于所用训练集中的数据实现合理的压缩结果，但是作为图像压缩器效果是不好的。 像JPEG这样的压缩技术效果比自编码器效果好很多。

自编码器经过训练，可以在输入通过编码器和解码器后保留尽可能多的信息，但也会接受训练以使新的表示具有各种不错的属性。 不同类型的自编码器旨在实现不同类型的属性。 我们将关注四种类型的自编码器。

▌自编码器的类型：

---

---

在本文中，将介绍以下四种类型的自编码器：

1.普通自编码器

2.多层自编码器

3.卷积自编码器

4.正则化的自编码

为了演示不同类型的自编码器，我使用Keras框架和MNIST数据集创建了每个类型自编码器的示例。 每种类型的自编码器的代码都可以在我的GitHub（https://github.com/Yaka12/Autoencoders）上找到。

• 普通自编码器

普通自编码器是三层网络，即具有一个隐藏层的神经网络。 输入和输出是相同的，我们将学习如何重构输入，例如使用adam优化器和均方误差损失函数。

在这里，我们看到我们有一个欠完备自编码器，因为隐藏层维（64）小于输入（784）。 这个约束将强加我们的神经网络来学习压缩的数据表示。

input_size = 784
hidden_size = 64
output_size = 784

x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='relu')(x)

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

• 多层自编码器

如果一个隐藏层不够用，我们显然可以将自编码器扩展到更多的隐藏层。

现在我们的实现使用3个隐藏层，而不是一个。 任何隐藏层都可以作为特征表示，但我们将使网络结构对称并使用最中间的隐藏层。

input_size = 784
hidden_size = 128
code_size = 64

x = Input(shape=(input_size,))

# Encoder
hidden_1 = Dense(hidden_size, activation='relu')(x)
h = Dense(code_size, activation='relu')(hidden_1)

# Decoder
hidden_2 = Dense(hidden_size, activation='relu')(h)
r = Dense(input_size, activation='sigmoid')(hidden_2)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

• 卷积自编码器

我们也可能会问自己：自编码器可以用于卷积层而不是全连接层吗？

答案是肯定的，原理是一样的，但使用图像（3D矢量）而不是平坦的1维矢量。 对输入图像进行下采样以提供较小尺寸的隐藏表示并强制自编码器学习图像的压缩版本。

x = Input(shape=(28, 28,1)) 

# Encoder
conv1_1 = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
pool1 = MaxPooling2D((2, 2), padding='same')(conv1_1)
conv1_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool1)
pool2 = MaxPooling2D((2, 2), padding='same')(conv1_2)
conv1_3 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool2)
h = MaxPooling2D((2, 2), padding='same')(conv1_3)


# Decoder
conv2_1 = Conv2D(8, (3, 3), activation='relu', padding='same')(h)
up1 = UpSampling2D((2, 2))(conv2_1)
conv2_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2, 2))(conv2_2)
conv2_3 = Conv2D(16, (3, 3), activation='relu')(up2)
up3 = UpSampling2D((2, 2))(conv2_3)
r = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up3)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

• 正则化的自编码器

还有其他一些方法可以限制自编码器的重构，而不是简单地强加一个维度比输入小的隐藏层。 正规化自编码器不是通过调整编码器和解码从而限制模型容量，而是使用损失函数，鼓励模型学习除了将输入复制到其输出之外的其他属性。 在实践中，我们通常会发现两种正规化自编码器：稀疏自编码器和去噪自编码器。

稀疏自编码器：稀疏自编码器通常用于学习分类等其他任务的特征。 稀疏自编码器必须响应数据集独特的统计特征，而不仅仅是作为标识函数。 通过这种方式，用稀疏性惩罚来执行复制任务的训练可以产生有用的特征模型。

我们可以限制自编码器重构的另一种方式是对损失函数施加约束。 例如，我们可以在损失函数中添加一个修正术语。 这样做会使我们的自编码器学习数据的稀疏表示

注意在我们的正则项中，我们添加了一个l1激活函数正则器，它将在优化阶段对损失函数应用一个惩罚。 在结果上，与正常普通自编码器相比，该表示现在更稀松。

input_size = 784
hidden_size = 64
output_size = 784

x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='relu', activity_regularizer=regularizers.l1(10e-5))(x)

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

去噪自编码器：我们可以获得一个自编码器，通过改变损失函数的重构误差项来学习一些有用的东西，而不是对损失函数加以惩罚。 这可以通过给输入图像添加一些噪声并使自编码器学会移除噪声从而来进行训练。 通过这种方式，编码器将提取最重要的特征并学习数据的更鲁棒的表示。

x = Input(shape=(28, 28, 1))

# Encoder
conv1_1 = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
pool1 = MaxPooling2D((2, 2), padding='same')(conv1_1)
conv1_2 = Conv2D(32, (3, 3), activation='relu', padding='same')(pool1)
h = MaxPooling2D((2, 2), padding='same')(conv1_2)


# Decoder
conv2_1 = Conv2D(32, (3, 3), activation='relu', padding='same')(h)
up1 = UpSampling2D((2, 2))(conv2_1)
conv2_2 = Conv2D(32, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2, 2))(conv2_2)
r = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up2)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

▌总结

---

---

在本文中，我们介绍了autoencoders的基本体系结构。我们还研究了许多不同类型的自编码器：普通自编码器，多层自编码器，卷积自编码器和正则化自编码器。 根据约束的不同（缩小隐藏层的尺寸或施加其他类型的惩罚项），可以学到不同属性的编码。

参考链接：

https://towardsdatascience.com/deep-inside-autoencoders-7e41f319999f

https://github.com/Yaka12/Autoencoders

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！

点击“阅读原文”，使用专知