ICML 2020 | 摆脱warm-up!巧置LayerNorm使Transformer加速收敛

编者按:Transformer 网络结构存在 warm-up 阶段超参数敏感、优化过程收敛速度慢等问题。为此,中科院、北京大学和微软亚洲研究院机器学习组的研究员们在 ICML 2020 的最新论文[1]中,从理论上分析了 Transformer 优化困难的原因,并提出了让 Transformer 摆脱 warm-up 阶段并加快收敛速度的解决方法。
近年来,Transformer 网络结构已经在自然语言处理的各项任务中都取得了“屠榜”的成绩。然而 Transformer 结构的优化非常困难,其具体表现有 warm-up 阶段超参数敏感、优化过程收敛速度慢等问题。近日,中科院、北京大学和微软亚洲研究院的研究员们在国际机器学习大会 ICML 2020 上发表了题为“On the Layer Normalization in the Transformer Architecture”的论文(点击阅读原文查看),从理论上详细分析了 Transformer 结构优化困难的原因,并给出了解决方法,可以让 Transformer 彻底摆脱 warm-up 阶段,并且大幅加快训练的收敛速度。
在随机优化的理论中,学习率往往设置为常数或者逐渐衰减 (decay),从而保证算法的收敛,这种学习率的设置方法也与机器学习里很多任务上的实际经验类似,例如图像分类、语音识别等。然而,不管是设置学习率为常数还是使学习率逐渐衰减都不能让 Transformer 很好地收敛。
在优化 Transformer 结构时,除了设置初始学习率与它的衰减策略,往往还需要在训练的初始阶段设置一个非常小(接近0)的学习率,让它经过一定的迭代轮数后逐渐增长到初始的学习率,这个过程也被称作 warm-up 阶段。
Warm-up 是原始 Transformer 结构优化时的一个必备学习率调整策略。Transformer 结构对于 warm-up 的超参数(持续轮数、增长方式、初始学习率等)非常敏感,若调整不慎,往往会使得模型无法正常收敛。
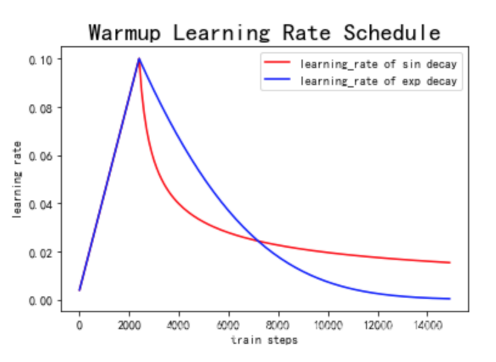
图1:常见的 warm-up 学习率策略
近日,来自伊利诺伊大学香槟分校的研究员们对 warm-up 问题进行了研究[2], 他们认为 Transformer 结构的优化中常用的 Adam 优化器[3](自适应学习率优化器的一种)在训练前期由于数据样本不足,导致自适应学习率在调整学习率时方差过大,从而引起优化稳定性不足,所以提出了 Rectified Adam(RAdam)算法来控制 Adam 优化器前期的方差。
我们在 IWSLT14 De-En 翻译数据集上使用 Transformer 模型对这一观点进行验证,采用 Adam 和 SGD 两种随机优化器,分别测试了两种学习率(1e^-3, 5e^-4)在没有 warm-up(0轮), warm-up 迭代轮数不足(500轮)和迭代轮数充足(4000轮)情况下模型的验证集 Loss 与 BLEU 分数。
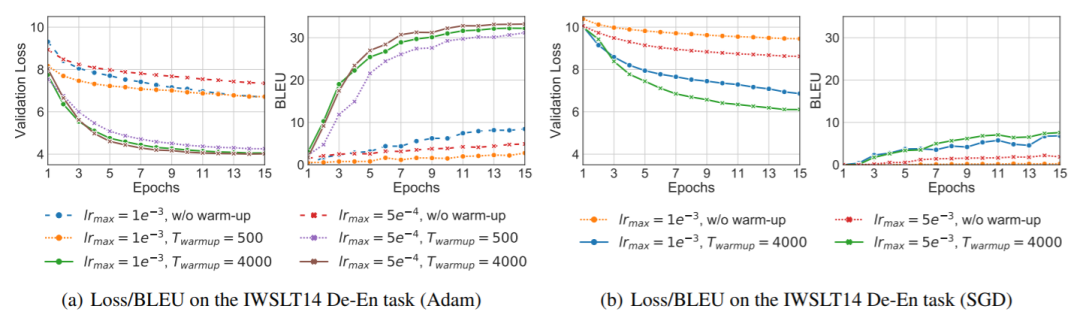
图2:IWSLT14 De-En 对比实验结果
从实验中可以看出:(1)模型最终性能对无论是 warm-up 所需迭代轮数还是学习率的大小都非常敏感;(2)不仅仅是自适应学习率方法 Adam, warm-up 方法对非自适应性学习率方法 SGD 也同样十分重要。由此看来,“自适应学习率在训练前期方差过大”这个解释并不能完全解答 Transformer 依赖 warm-up 的问题。
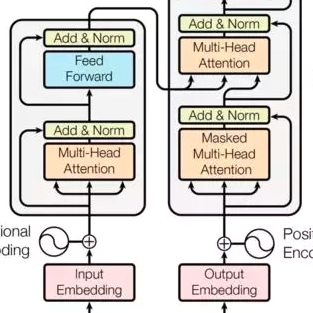
由于 Transformer 优化困难的阶段是在训练的初始阶段,warm-up 也只是在迭代的前若干轮起作用,因此我们从模型的初始化阶段开始探究原因。如图3(a)所示,原始 Transformer 结构的每一层中分别经过了带残差连接的 Multi-Head Attention 和 FFN 两个子层(sub-layer),在两子层之后分别放置了层归一化(Layer Normalization)层,即 Post-LN Transformer。
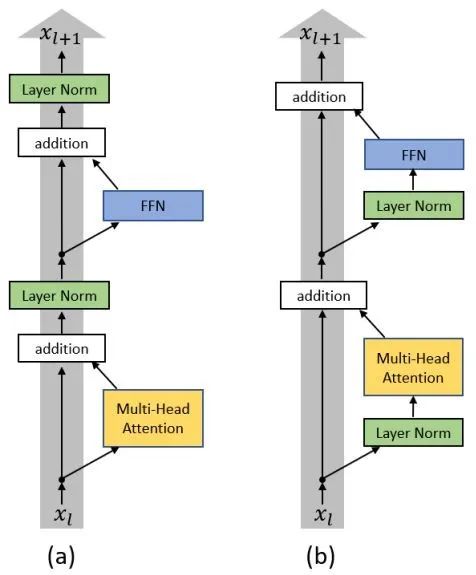
图3:(a) Post-LN Transformer;(b) Pre-LN Transformer
当采用 Xavier[4] 方法对 Post-LN Transformer 进行初始化后,通过对各隐层梯度值进行分析可以证明,在初始化点附近的 Post-LN Transformer 结构最后一层的梯度值非常大,同时随着反向传播的前传会导致梯度值迅速衰减。这种在各层之间不稳定的梯度分布必然会影响优化器的收敛效果,导致训练过程初始阶段的不稳定。造成 Post-LN Transformer 梯度分布出现问题的核心原因在于各子层之后的 Layer Normalization 层会使得各层的输入尺度与层数 L 无关,因此当 Layer Normalization 对梯度进行归一化时,也与层数 L 无关。
将 Layer Normalization 放到残差连接中的两个子层之前,并且在整个网络最后输出之前也增加一个 Layer Normalization 层来对梯度进行归一化,我们称这样的结构为 Pre-LN Transformer[5][6],如图3(b)所示。
使用相同的方法对 Pre-LN Transformer 结构进行分析后,发现最后一层 Layer Normalization 层的输入尺寸的量级只有 Post-LN 的√(1/L)倍,并且每个 LN 层都会对梯度以 √L 的比例归一化。所以对于 Pre-LN 结构来说,其每层梯度范数都近似不变。
我们在 IWSLT 14 De-En 数据集对两种结构在初始化附近以及经过了 warm-up 阶段的梯度范数进行了验证:
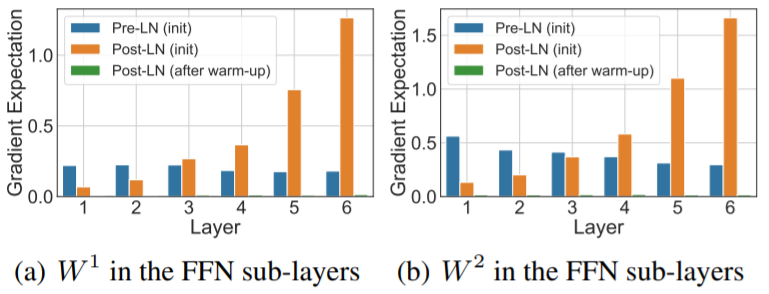
图4:梯度范数验证实验
可以看出,相比于 Post-LN 结构梯度分布的不稳定,Pre-LN 在各层之间梯度范数几乎保持不变,这种结构明显更利于优化器进行优化。而在进行一定轮数的 warm-up 后,Post-LN 的梯度范数也基本保持不变,并且其量级非常小(图4中绿色),这也验证了我们的结论。
在 IWSLT、WMT 和 BERT 三个任务上验证了是否可以在 Pre-LN 结构中去掉 warm-up:
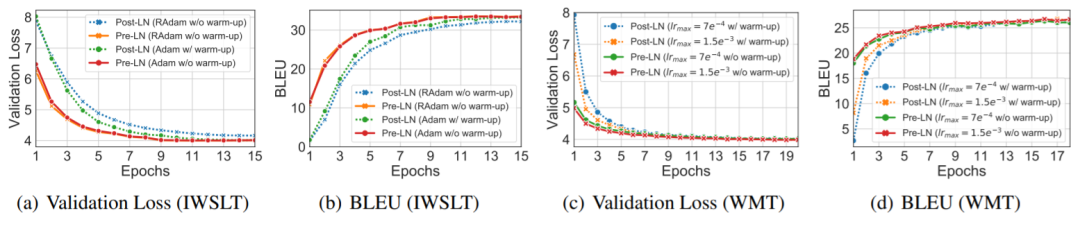
图5:IWSLT 与 WMT 实验结果
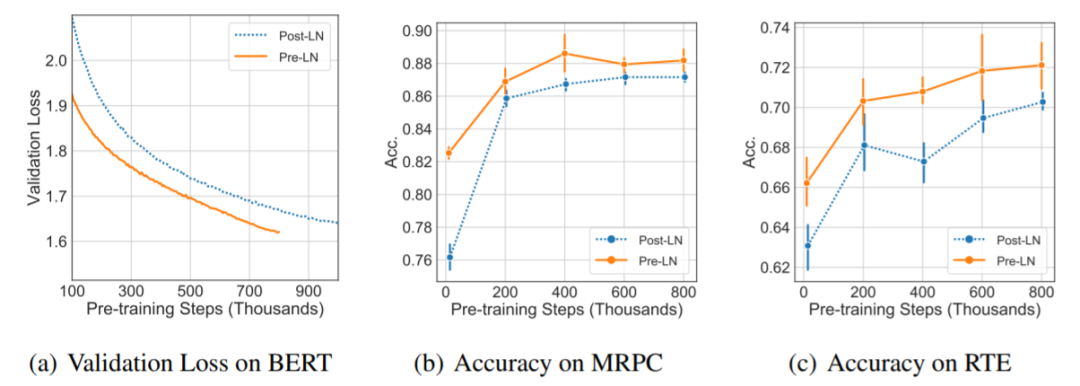
图6:BERT 验证集 Loss 与下游任务表现
我们发现,当使用 Pre-LN 结构时,warm-up 阶段已经不再是必需,并且 Pre-LN 结构可以大幅提升 Transformer 的收敛速度。对于机器翻译任务(IWSLT/WMT),不需要 warm-up 的 Pre-LN 结构可以比 Post-LN 收敛快1倍左右,而在 BERT 上,Pre-LN 在下游任务上达到和 Post-LN 相同的性能也只需要后者迭代轮数的1/3左右,并且最终的效果也更好。
至此,我们通过对 warm-up 问题的本质进行分析,不仅彻底摆脱了恼人的 warm-up 以及敏感的调参过程,还令 Transformer 结构的训练过程更稳定,收敛速度也更快。
参考文献
[1] Ruibin X, Yunchang Y, Di H, et al. On Layer Normalization in the Transformer Architecture. ICML 2020
[2] Liu L, Jiang H, He P, et al. On the variance of the adaptive learning rate and beyond. ICLR 2019.
[3] Kingma D P, Ba J. Adam: A method for stochastic optimization[J]. arXiv preprint arXiv:1412.6980, 2014.
[4] Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the thirteenth international conference on artificial intelligence and statistics. 2010: 249-256.
[5] Baevski, A. and Auli, M. Adaptive input representations for neural language modeling. arXiv preprint arXiv:1809.10853, 2018.
[6] Child, R., Gray, S., Radford, A., and Sutskever, I. Generating long sequences with sparse transformers. arXiv preprint arXiv:1904.10509, 2019.
你也许还想看: