绝对干货 | 随机梯度下降算法综述

本文讲述了“随机梯度下降算法综述”，起源于一篇英文论文，国内也有人专门翻译过，现在在公开课上遇到了，重新温习了一次，故记录下来。链接见文末。

~开始~

菜鸟说：公开课的脉络与原文结构保持了一致。

~

菜鸟说：梯度下降法一般分为两步：第一、求梯度，第二、选择合适的学习率。

~

菜鸟说：学习率的选择比较麻烦，在实践中很多的也是尝试，经验发挥较大作用，故自适应学习率才是王道。

~

菜鸟说：批梯度下降法时间复杂度较高，但稳定性好；随机梯度下降法稳定性差，但时间复杂度较低。所以，小批量随机梯度下降法是批梯度下降法和随机梯度下降法的一种折衷，在工程中也是最为主流的使用方法。

菜鸟说：不稳定性也需一分为二看待，优点：增加了跳出当前局部极小值的可能性；缺点：可能会降低收敛速度，亦受噪音影响。不稳定性不一定会带来好的结果，但带来了好的结果的可能性。

菜鸟说：小批量如何选择呢？有文章说明在几十到几百之间，但与具体应用场景有很大关系。切记：训练之前，训练样本一定要shuffle。

~

菜鸟说：小批量随机梯度下降法也不是万能的，单独使用也会出现各种各样的问题，需要与其他技术相配合。

菜鸟说：缺点3中意思就是有些特征在训练样本中稀少，有些特征在训练样本很多，若采用相同的学习率，特征少的学习会很不充分，应该采用较大的学习率。

菜鸟说：学习率，自适应学习率+多样性学习率是王道，老铁，没毛病。

菜鸟说：缺点4中在鞍点附近会比较平滑，训练过程中若遇到鞍点，很难逃离了。

~

菜鸟说：牛顿法是二阶收敛，采用二阶泰勒展现去逼近，收敛速度很快，但时间复杂度、空间复杂度较大。

菜鸟说：在实际应用中，与其遇到鞍点，还不如遇到局部最小值点。

下面正式开始介绍实际应用中解决上述问题的方法

~

菜鸟说：梯度下降法会在隧道两侧来回震荡，降低收敛速度。

~

菜鸟说：从更新公式看出，不仅考虑当前的梯度，还考虑以前的余势。

菜鸟说：例如，t-1时刻是往右走，t时刻也是往右走，这样就加速了往右走的速度。

~

菜鸟说：动量法的问题在于到达山底停不下来，又跑到了另一侧。为了避免这种问题，于是就有了NAG。

~

菜鸟说：自适应+多样化的更新学习率。

~

菜鸟说：对于稀疏数据来说，Adagrad效果比较好。它主要考虑历史梯度平方和，即为Grad_Sum，若Grad_Sum大， 说明该特征更新较为频繁，这样学习率应该更小些；若Grad_Sum小，说明该特征更新较为不频繁，这样学习率应该大一些。但总体都是衰减的。

~

菜鸟说：AdaGrad的问题在于每次更新学习率都会衰减，如果衰减到非常小，会造成收敛速度降低，甚至不收敛。所以Adadelta则使用梯度平方的移动平均来取代全部历史平方和，更多考虑距离当前更新近的梯度来作为学习率衰减程度的因素。

菜鸟说：Adadelta有一篇论文，可以看下。

~

菜鸟说：RMSprop更牛逼，初始学习率都不用选择了，当然，量纲也保持一致了，哈哈。

~

~

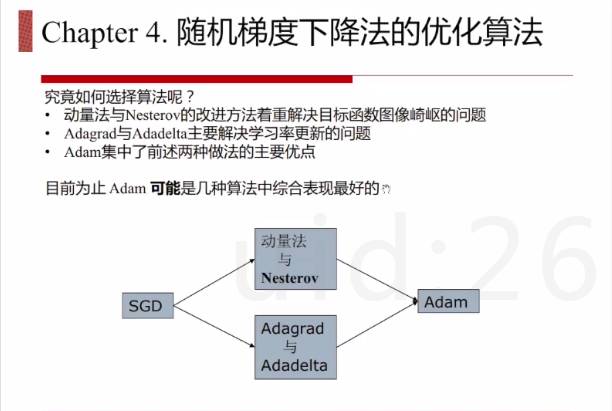
菜鸟说：如何根据数据选择相应的优化算法呢？应该从问题本身的特点来选择不同的算法。我实践中应用过动量法+Adagrad+Adadelta，Adam还真没有用过，也没有见人用过，囧。

菜鸟说：感觉可以看模型指标，然后通过交叉验证去选择。

~

~

菜鸟说：除了从算法角度优化随机梯度下降，也可以从其他的角度去考虑。

菜鸟说：批规范化主要针对多层神经网络，同理，批再规范化也类似。

~结束~

原文题目：An overview of gradient descent optimization algorithms

原文链接：http://sebastianruder.com/optimizing-gradient-descent

视频地址：http://www.julyedu.com/video/play/69/646

---