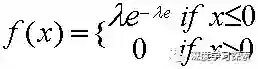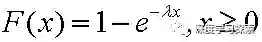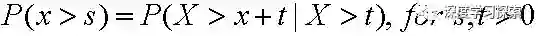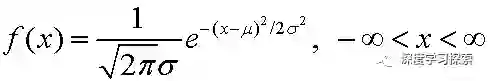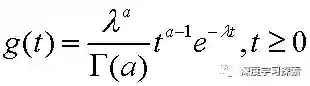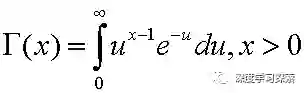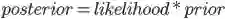概率06——连续分布

在随机变量中，我提到了连续随机变量。相对于离散随机变量，连续随机变量可以在一个连续区间内取值。比如一个均匀分布，从0到1的区间内取值。一个区间内包含了无穷多个实数，连续随机变量的取值就有无穷多个可能。

为了表示连续随机变量的概率分布，我们可以使用累积分布函数或者密度函数。密度函数是对累积分布函数的微分。连续随机变量在某个区间内的概率可以使用累积分布函数相减获得，即密度函数在相应区间的积分。

在随机变量中，我们了解了一种连续分布，即均匀分布(uniform distribution)。这里将罗列一些其他的经典连续分布。

 

指数分布

---

 

指数分布(exponential distribution)的密度函数随着取值的变大而指数减小。指数分布的密度函数为:

 

累积分布函数为:

 

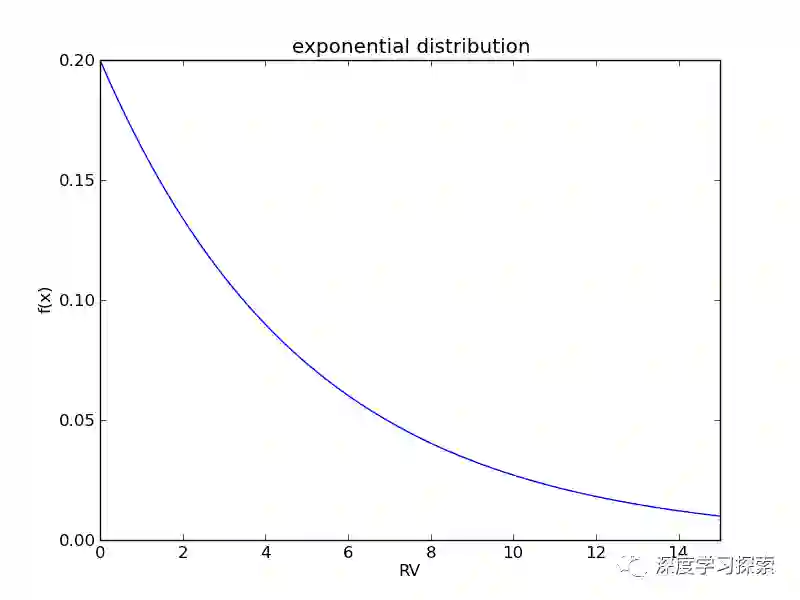
我们绘制一个指数分布$=0.2\lambda =0.2，如下:$

这样一种分布在生活中很常见。比如，洪水等级的分布就类似于这样一个分布。小等级的洪水常发生，而大洪水发生的概率则很小。再比如，金矿的分布：大部分矿石的含金量少，而少部分矿石的含金量高。这提醒我们，一些特殊的条件导致了指数分布。感兴趣的话可以学习“随机过程”这一数学分支。

指数分布是无记忆(memoryless)的。我们以原子衰变为例。任意时刻往后，都需要10年的时间，会有一半的原子衰变。已经发生的衰变对后面原子衰变的概率分布无影响。用数学的语言来说，就是

 

 

 

  

等式的左边是原子存活了s的概率。而等式的右边是某一时刻t之后，原子再存活s时间的概率。可以利用指数分布的累积分布函数，很容易的证明上面的等式。指数分布经常用于模拟人的寿命或者电子产品的寿命，这意味着我们同样假设这些分布是无记忆的。一个人活10年的概率和一个人到50岁后，再活10年的概率相等。这样的假设有可能与现实情况有所出入，需要注意。

 

正态分布

---

 

正态分布(normal distribution)是最常用到的概率分布。正态分布又被称为高斯分布(Gauss distribution)，因为高斯在1809年使用该分布来预测星体位置。吐槽一句，第一个提出该分布的并不是数学王子高斯，而是法国人De Moivre。作为统计先驱，这位数学家需要在咖啡馆“坐台”，为赌徒计算概率为生。(看来法国咖啡馆不止有文艺青年，也有技术屌丝啊。)

Abraham De Moivre

 

Gauss

 

正态分布的发现来自于对误差的估计。早期的物理学家发现，在测量中，测量值的分布很有特点：靠近平均值时，概率大；远离平均值时，概率小。比如我们使用尺子去测量同一个物体的长度，重复许多次。如果没有系统误差，那么测量到的长度值是一个符合正态分布的随机变量。再比如，在电子信号中白噪音，也很有可能符合正态分布。De Moivre最早用离散的二项分布来趋近这一分布，而高斯给出了这一分布的具体数学形式。

正态分布自从一出生就带着无比强大的“主角光环”，它的特殊地位在后面文章中的中心极限定理中凸显出来。

正态分布的密度函数如下:

正态分布有两个参数，μ和σ。我们可以将正态分布表示成N(μ,σ)。当μ=0,σ=1，这样的正态分布被称作标准正态分布(standard normal distribution)。

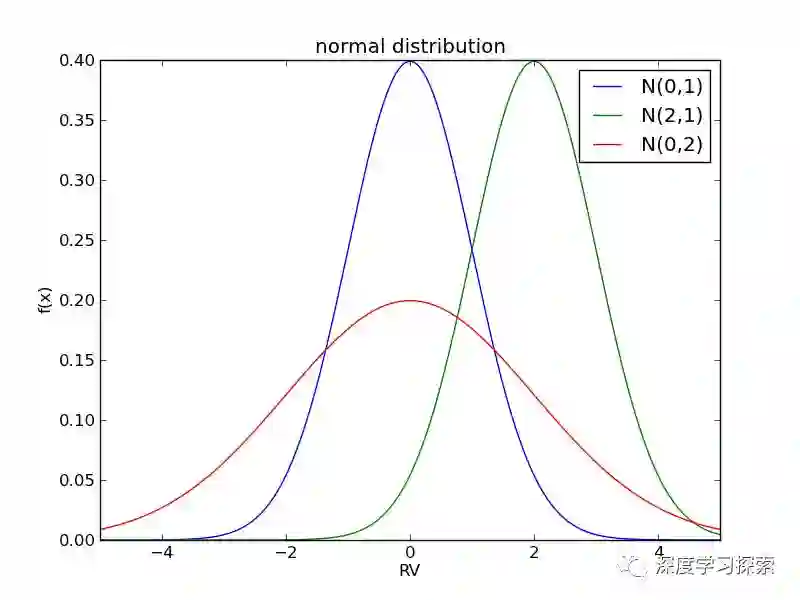
我们绘制三个正态分布的密度函数:

可以看到，正态分布关于x=μ对称，密度函数在此处取得最大值，并随着偏离中心而递减。如果以测量长度为例，这说明的读取值靠近
μ的可能性较大，而偏离μ的可能性变小。

σ代表了概率分布的离散程度。σ越小，概率越趋近对称中心x=μ。

 

Gamma分布

---

 

Gamma分布在统计推断中具有重要地位。它的密度函数如下:

其中的Gamma函数可以表示为:

注意到，Gamma分布有两个控制参数α和λ。

 

贝塔分布

---

在介绍贝塔分布(Beta distribution)之前，需要先明确一下先验概率、后验概率、似然函数以及共轭分布的概念。

• 先验概率就是事情尚未发生前，我们对该事发生概率的估计。利用过去历史资料计算得到的先验概率，称为客观先验概率； 当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率，称为主观先验概率。例如抛一枚硬币头向上的概率为0.5，这就是主观先验概率。

• 后验概率是指通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的概率。

• 先验概率和后验概率的区别：先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料。另外一种表述：先验概率是在缺乏某个事实的情况下描述一个变量；而后验概率（Probability of outcomes of an experiment after it has been performed and a certain event has occured.）是在考虑了一个事实之后的条件概率。

• 似然函数

• 共轭分布(conjugacy)：后验概率分布函数与先验概率分布函数具有相同形式

好了，有了以上先验知识后，终于可以引入贝塔分布啦！！首先，考虑一点，在试验数据比较少的情况下，直接用最大似然法估计二项分布的参数可能会出现过拟合的现象（比如，扔硬币三次都是正面，那么最大似然法预测以后的所有抛硬币结果都是正面）。为了避免这种情况的发生，可以考虑引入先验概率分布p(μ)来控制参数μ，防止出现过拟合现象。那么，问题现在转为如何选择p(μ)！先验概率和后验概率的关系为：

二项分布的似然函数为（就是二项分布除归一化参数之外的后面那部分，似然函数之所以不是pdf，是因为它不需要归一化）：

μ^m(1-μ)ⁿ 

如果选择的先验概率p(μ)也与μ和(1-μ)次方的乘积的关系，那么后验概率分布的函数形式就会跟它的先验函数形式一样了。具体来说，选择prior的形式是

ω₁*μ^m(1-μ)ⁿ

那么posterior就会变成

ω₂*μ^m+a(1-μ)^n+b

这个样子了(ω1, ω2为pdf的归一化参数)，所以posterior和prior具有相同的函数形式(都是p(μ)也与μ和(1-μ)次方的乘积),这样先验概率与后验概率就是共轭分布了。所以，我们选择了贝塔分布作为先验概率，其概率分布函数为：

总结

---

 

我们研究了四种连续随机变量的分布，并使用概率密度函数的方法来表示它们。密度函数在数学上比较容易处理，所以有很重要的理论意义。

密度函数在某个区间的积分，是随机变量在该区间取值的概率。这意味着，在密度函数的绘图中，概率是曲线下的面积。

如果你也无基础想研究深度学习

长按上方二维码

立即关注

深度学习探索微信：mydeeplearning