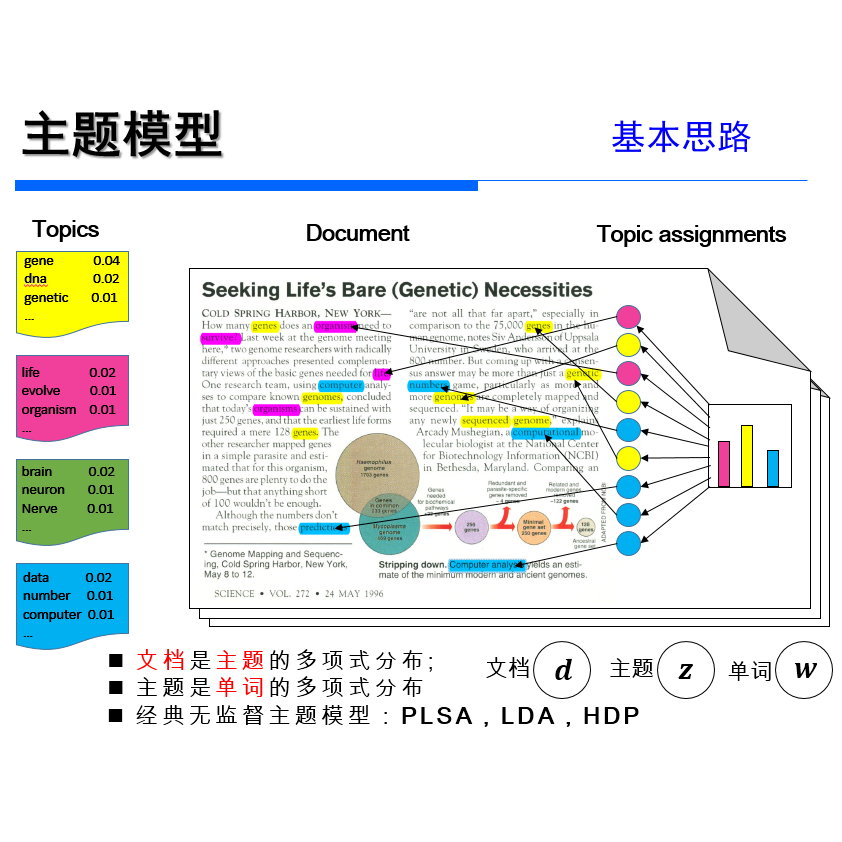
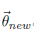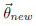基于LDA的主题模型实践(二 )MCMC--吉布斯采样
上篇文章废了九牛二虎之力花了好多篇幅好容易把LDA主题模型联合概率分布推导出来,然壮士空有报国伟大愿惋惜无回天之屠龙宝刀,有了概率分布要如何从输入文档中求解抽取出我们想要得到的文档主题分布和主题词袋分布呢。下面我们由LDA联合分布到达彼岸文档“主题—分布”和“主题—词”分布利用的吉布斯抽样方法。吉布斯抽样数与蒙特卡洛马尔科夫链(MCMC)一个特殊抽样解决算法,所以下文会先给各位看官介绍MCMC算法,然后引出吉布斯抽样,最后以LDA吉布斯抽样求解作为例子结尾。
MCMC简介
随机模拟方法是通过随机变量函数的概率模拟、统计实验或随机抽样求解数学物理、工程技术、生产管理等各种不同问题的近似数值解的概率统计方法。
利用大数定理抽取足够多的样本取均值,逼近所求值的近似求解方法。
MC基本思路
1) 针对实际问题建立一个简单且便于实现的概率统计模型,使所求的解恰好是所建模型的概率分布或某个数字特征,比如是某个事件的概率,或者是该模型的期望值。
2) 对模型中的随机变量建立抽样方法,在计算机上进行模拟试验,抽取足够的随机数,并对有关的事件进行统计。
3) 对模拟试验结果加以分析,给出所求解的估计及其精度(方差)的估计。
4) 改进模型以降低估计方差和优化算法步骤,提高模拟计算的效率
特殊MCMC
MC方法的一个基本步骤是产生随机数,使之服从一个概率分布π(X).当X是一维的情况时,这很容易做到。当X取值域实数域多维下向量,直接产生符合π的独立样本是行不通,往往样本要么不独立,要么不符合π,或者两者都有。最常用的解决办法MCMC,Metropolis方法和Hastings的概括奠定MCMC方法的基石。此方法就是在以π为平稳分布的马氏链上产生相互依赖的样本。MCMC是MC综合程序,它的随机样本的产生与一条马氏链有关。
基于条件分布的迭代取样是另一种重要的MCMC方法,其中最著名的特殊情况就是吉布斯抽样。其潜在的马氏链是通过分解一些列条件建立起来。通过建立一个平稳分布为π(x)的马氏链来得到π(x)的样本,基于这些样本做各种统计推断。
例: 假设状态空间是(雨、晴、阴),并且天气变化过程是一个马氏过程,这样,明天天气的概率仅依赖今天的天气,与以前的无关。假如已知今天是雨的情况下的转移概率是
P(雨|雨)=0.5 , P(晴|雨)=0.25 ,P(阴|雨)=0.25
这样转移概率矩阵的第一行为(0.5,0.25,0.25)
如此假设转移概率矩阵为
所有状态之间都是有联系的,因此这个马氏链是不可约的。假设今天是晴,那么2天后与7天后的天气可如下给出,这儿π(0) = (0,1,0)
如果假设今天是雨,即π(0) = (1,0,0),则有π(2) = (0.4375,0.1875,0.75)和π(0) = (0.4,0.2,0.4)
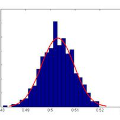
实际上,经过一个充分长的时间,期望的天气与初始状态无关,达到马氏链平衡状态,这儿的概率值与初始值是独立的。一个马氏链可能达到一个平稳分布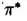
平稳分布的条件是马氏链是不可约非周期的,当马氏链是周期的,它会在状态之间以一个稳定的方式循环。是平稳分布的一个充分条件是下面的细致平衡条件成立
如果对所有i,k都有上述方程成立,就说马氏链是可逆的。记
为πP的第J个元素则
最后一个等式利用了转移矩阵每行元素的和为1离散状态的马氏链的基本思想可以推广到连续情形,设其转移核为P(x,y)
相应的平稳分布满足:
吉布斯抽样
吉布斯抽样是一种基于条件分布的迭代取样方法。这样就要用到条件分布,特别是满足条件分布。所谓满足条件分布就是形如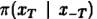
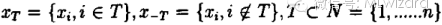
在上述条件分布中,所有的变量全部出现(出现在条件中,或出现在变元中)。考虑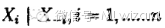
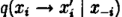
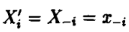
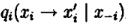
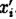
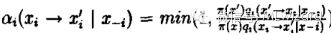
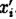
其中
而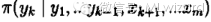
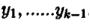
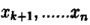
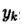
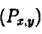
可验证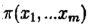
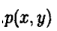
吉布斯抽样具体步骤:
由马氏链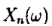
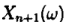
1)先得到服从分布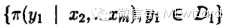
(注意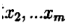
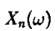
2)在得到服从分布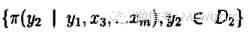
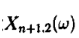
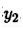
的随机变量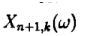
3)得到服从分布
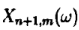
流程如下:
实例:
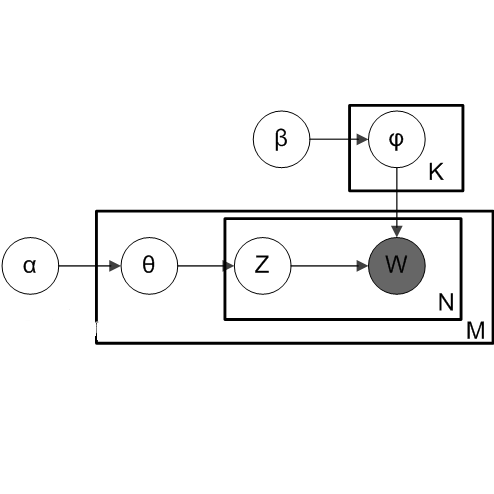
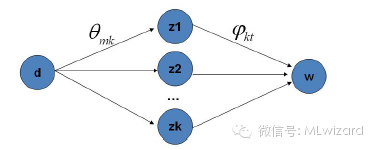
LDA主体分文本聚类,根据上章模型主题模型建立得到主题模型的联合概率分布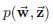
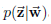
o Gibbs Sampling算法的运行方式是每次选取概率向量的一个维度,给定其他维度的变量值采样当前维度的值。不断迭代,直到收敛输出待估计的参数。
o 初始时随机给文本中的每个单词分配主题z(0),然后统计每个主题z下出现term t的数量以及每个文档m下出现主题z中的词的数量,每一轮计算p(zi|z-i,d,w),即排除当前词的主题分配:根据其他所有词的主题分配估计当前词分配各个主题的概率。当得到当前词属于所有主题z的概率分布后,根据这个概率分布为该词采样一个新的主题。然后用同样的方法不断更新下一个词的主题,直到发现每个文档下Topic分布θ和每个Topic下词的分布φ收敛,算法停止,输出待估计的参数θ和φ,最终每个单词的主题zmn也同时得出。
o 实际应用中会设置最大迭代次数。每一次计算p(zi|z-i,d,w)的公式称为吉布斯迭代更新规则.
联合分布如下:
o 第一项因子是给定主题采样词的过程
o 后面的因子计算,nz(t)表示term t被观察到分配topicz的次数, nm(t)表示topic k分配给文档m中的word的次数。
计算因子:

其中:
得出吉布斯更新规则如下:
其中词主题和分布:
最终我们得到LDA的吉布斯采样公式:
右边是P(topic|doc).p(word|topic),这个概率其实是doc—〉topic—〉word的路径概率,由于topic有k歌,所以吉布斯抽样公式的物理意义就是在这K条路径进行采样。
LDA训练:
有了LDA模型,我们目标有两个
估计模型中参数
和
对于新来的一篇文章,能够计算这篇文档的topic分布
统计文档中topic分布,该分布就是1、 随机初始化:对当前文档中的每个词W,随机的赋一个topic编号z;
2、 扫描当前文档,按照吉布斯抽样公式,对每个词w,重新采样它的topic
3、 重复以上过程知道吉布斯抽样收敛;
4、统计文档中topic分布,该分布就是

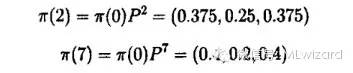
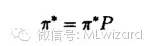
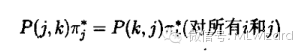
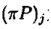
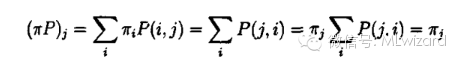
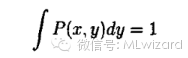
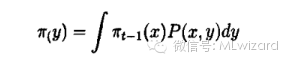
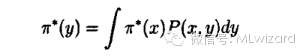
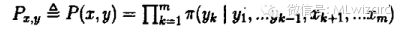
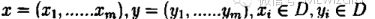
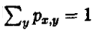
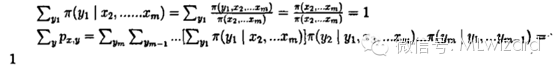
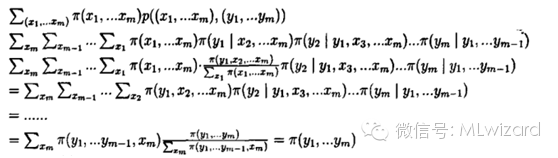
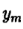

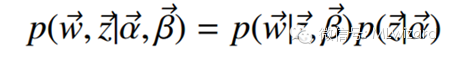



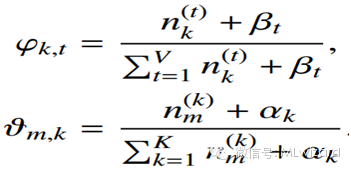
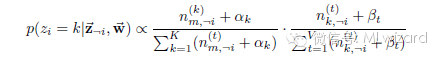
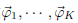 和
和