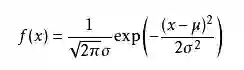干货 | 一文搞懂极大似然估计

极大似然估计，通俗理解来说，就是在假定整体模型分布已知，利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

可能有小伙伴就要说了，还是有点抽象呀。我们这样想，一当模型满足某个分布，它的参数值我通过极大似然估计法求出来的话。比如正态分布中公式如下：

如果我通过极大似然估计，得到模型中参数u和sigma的值，那么这个模型的均值和方差以及其它所有的信息我们是不是就知道了呢。确实是这样的。

极大似然估计中采样需满足一个重要的假设，就是所有的采样都是独立同分布的。

下面我通过俩个例子来帮助理解一下最大似然估计

例子一

别人博客的一个例子。

假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。

现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球 再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？

很多人马上就有答案了：70%。而其后的理论支撑是什么呢？

我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜色服从同一独立分布。

这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的,三十次为黑球事件的概率是P(样本结果|Model)。

如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样，我们可以得到如下表达式：

P(样本结果|Model)

　　= P(x1,x2,…,x100|Model)

　　= P(x1|Mel)P(x2|M)…P(x100|M)

　　= p^70(1-p)^30.

好的，我们已经有了观察样本结果出现的概率表达式了。那么我们要求的模型的参数，也就是求的式中的p。

那么我们怎么来求这个p呢？按照什么标准来求这个p呢？

不同的p，直接导致P（样本结果|Model）的不同。

好的，我们的p实际上是有无数多种分布的。如下：

那么在上面p的分布条件下求出 p^70(1-p)^30为 7.8 * 10^(-31)

p的分布也可以是如下：

那么也可以求出p^70(1-p)^30为2.95* 10^(-27)

那么问题来了，既然有无数种分布可以选择，极大似然估计应该按照什么原则去选取这个分布呢？

答：采取的方法是让这个样本结果出现的可能性最大，也就是使得p^70(1-p)^30值最大，那么我们就可以看成是p的方程，求导即可！

那么既然事情已经发生了，为什么不让这个出现的结果的可能性最大呢？使得发生的样本出现的可能性最大。这就是最大似然估计的核心。

我们想办法让观察样本出现的概率最大，转换为数学问题就是使得：

p^70(1-p)^30最大，这太简单了，未知数只有一个p，我们令其导数为0，即可求出p为70%，与我们一开始认为的70%是一致的。其中蕴含着我们的数学思想在里面。

 例子二

假设我们要统计全国人民的年均收入，首先假设这个收入服从服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的收入。我们国家有10几亿人口呢？那么岂不是没有办法了？

不不不，有了极大似然估计之后，我们可以采用嘛！我们比如选取一个城市，或者一个乡镇的人口收入，作为我们的观察样本结果。然后通过最大似然估计来获取上述假设中的正态分布的参数。

有了参数的结果后，我们就可以知道该正态分布的期望和方差了。也就是我们通过了一个小样本的采样，反过来知道了全国人民年收入的一系列重要的数学指标量！

那么我们就知道了极大似然估计的核心关键就是对于一些情况，样本太多，无法得出分布的参数值，可以采样小样本后，利用极大似然估计获取假设中分布的参数值。就相当于得到了模型的一系列重要数学指标了。

参考：

从最大似然到EM算法浅解 - zouxy09的专栏 - 博客频道 - CSDN.NET

最大似然估计的学习 - growoldwith_you的博客 - 博客频道 - CSDN.NET

热文精选

何恺明团队推出Mask^X R-CNN，将实例分割扩展到3000类

AI人才缺失催生的“跨境猎头”，人才年薪高达300万，猎头直赚100万

如何成为一名全栈语音识别工程师？

Twitter大牛写给你的机器学习进阶手册

AI研究生应届生年薪可达50万 没出校门已被"抢光

深度学习高手该怎样炼成？这位拿下阿里天池大赛冠军的中科院博士为你规划了一份专业成长路径

专访图灵奖得主John Hopcroft：中国必须提升本科教育水平，才能在AI领域赶上美国

2017年首份中美数据科学对比报告，Python受欢迎度排名第一，美国数据工作者年薪中位数高达11万美金