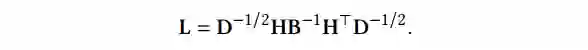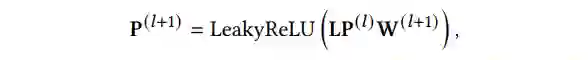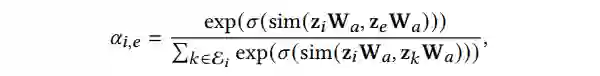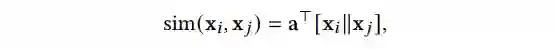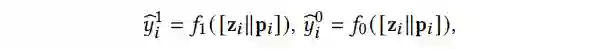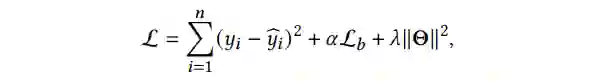KDD最佳论文又又又颁给了GNN。。。

©PaperWeekly 原创 · 作者 | 张三岁

研究方向 | 图神经网络

论文标题：

Learning Causal Effects on Hypergraphs

论文作者：

Jing Ma, Mengting Wan, Longqi Yang, Jundong Li, Brent Hecht, Jaime Teevan

收录会议：

KDD 2022 Best Paper

论文链接：

https://arxiv.org/abs/2207.04049

Background

个人（individual）间的群体互动（Group interaction）广泛存在，比如大规模的聚会、WhatsApp 或微信上的日常群聊（group chat）以及微软团队或 Slack 频道上的工作交际（workplace interaction）。尽管传统图（pairwise graph）的定义涵盖了大部分的应用场景（例如人与人之间的物理接触或社交网络），但它不能捕捉到群体互动（group interaction）的信息（即每个互动会涉及两个以上的人）。

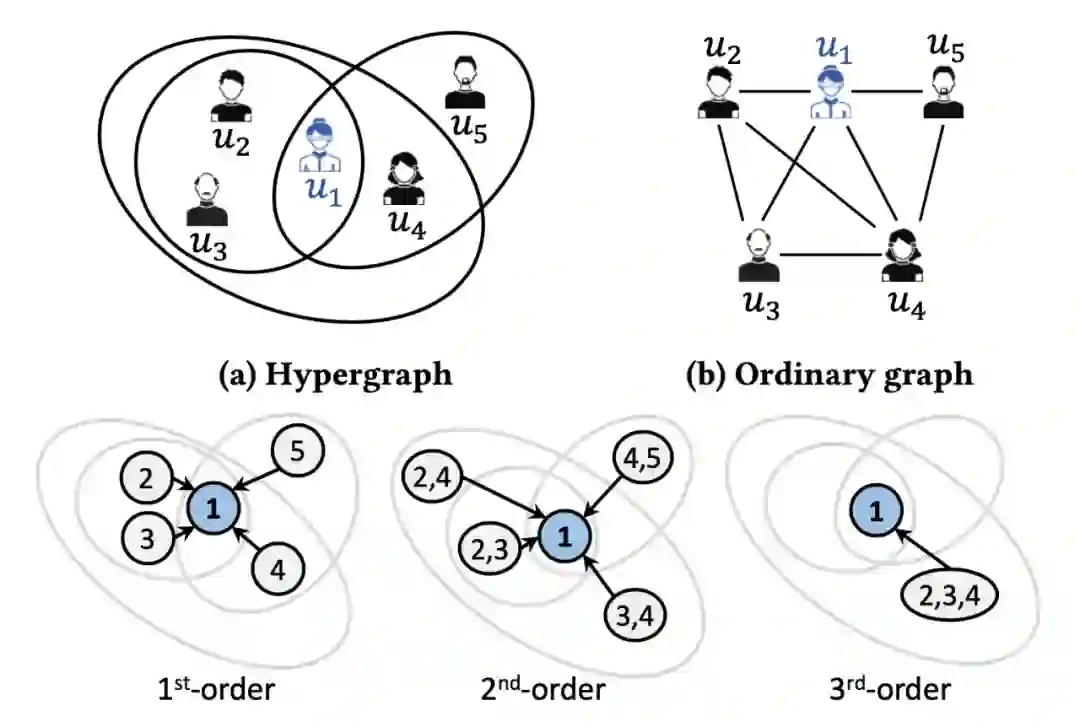
由此，我们引入超图（hypergraph）的概念来解决这个问题。以图 1(a) 所示的超图为例，每个人（individual）通过面对面的社交活动建立连接，而每个把人聚集起来的活动可以被表示为一个超边（hyperedge）。每个超边（hyperedge）可以连接任意数量的人（individual）/节点，而普通图的边，如图 1(b) 所示，则只能连接两人/节点。

▲ 图1

Motivation

虽然许多研究都致力于利用这样一个超图（hypergraph）结构来促进机器学习任务，但它们中的大多数仍是在统计相关性（statistical correlation）的角度进行研究。例如，通过捕捉一个人（individual）的人口信息（即节点特征 node features）、团体聚会史（超图结构 hypergraph structure）和感染结果（节点标签 node labels）之间的相关性来预测每个人（节点 node）的 COVID-19 感染风险。

这类研究方法的一个局限性在于缺乏因果性（causality），而因果性对于了解政策干预（如：戴口罩）对结果（如：感染 COVID-19）的影响尤为重要。例如，对图 1(a) 中相连的个体（individual），有人可能会问：“个人是否戴口罩（实验 treatment）会如何在因果关系上影响其感染风险（结果 outcome）？”

所以，这篇文章想要探索在超图上进行因果推断任务的学习。具体来说， 这篇文章专注于从观察数据中估计在超图干涉（hypergraph interference）下的个体实验效果（individual treatment effect ITE）。

Challenge

但如 motivation 中所述的因果推断任务需要保持除实验变量（treatment variable）外所有其他可能的因素不变，从而构建同一个个体的反事实状态（counterfactual state）。这在超图（hypergraph）数据上是一个特别困难的问题，因为个人的结果（outcome) 不仅受到他们自己（如个人的健康状况和疫苗状态）的影响（confounding factor），而且还受到超图（hypergraph）上其他个体的影响（如与目标个体通过聚会有物理接触的其他个体是否戴口罩），具体可分为如下两点：

1. 随机实验的实证限制（Empirical constraints of randomized experiments）：估计实验效果（treatment effect estimation）最可靠的方法之一是进行随机对照试验（randomized controlled trials RCTs），然而进行 RCTs 实验通常成本高且不切实际，还会存在实验道德问题。此外，由于在图（graph）上的节点彼此间存在依赖性（dependency），我们很难在图上直接应用 RCTs 方法来估计实验效果。

2. 超图上高阶干涉（High-order interference on hypergraphs）的建模困难：ITE 估计问题（ITE estimation）的目标是估计某个实验 treatment（如戴口罩）对每个个体的结果 outcome（如 COVID-19 感染）的因果效应（causal effect）。

传统的 ITE 估计（ITE estimation）是基于稳定单位实验值（Stable Unit Treatment Value SUTVA）的假设。这个假设是指实例（instance）或单位（unit）之间不存在干涉（interference），即不存在溢出效应（spillover effect）。这意味着任何实例的结果（outcome）都不会受到其他实例的影响。这个假设在真实世界中是不现实的，特别是在实例间存在依赖性的图（graph） 上。

目前大部分试图解决这个问题的工作都认为干涉（interference）只以成对的（pairwise）方式存在于普通图（ordinary graph）上，如图 1(b) 所示。但这种成对的干涉不足以描述存在于超图（hypergraph）上的高阶干涉（high-order interference）。

如图 1(c) 所示，在 都参与的聚会（gathering event）中即它们在同一条超边（hyperedge）内，个体 的感染结果（outcome）会受到其一阶个体 的影响。我们将 , 这种影响称之为一阶干涉（first-order interference）。

此外，个体 的感染结果（outcome）还会受到其他个体之间相互作用的影响，即 和 间的相互作用也可能影响到病毒对 的暴露程度。我们将 这种二阶（second-order）互动效应的影响称之为高阶干涉（high-order interference）。

请注意，这种高阶干涉（high-order interference）项的数量会随着超图大小的增加而呈组合式地增长，导致原始超图和超图投影下的成对普通图（只考虑一阶干涉）之间出现明显的信息差。为了更好的利用超图进行因果推断，我们需要能够对高阶干涉进行建模的技术，然而在这一领域的工作很少。

Method

▲ 图2

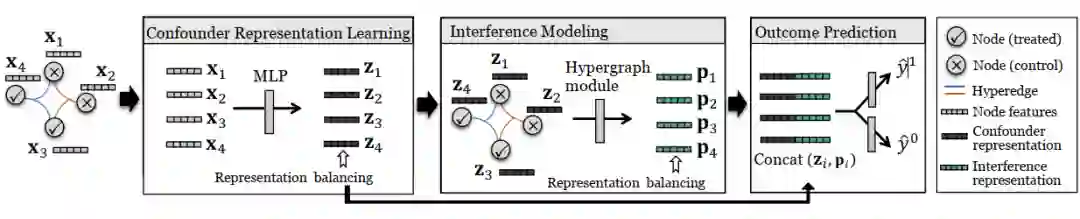
为了对高阶干涉进行建模从而在超图上进行因果推断任务，这篇文章提出了一个新的框架 Causal Inference under Spillover Effects in Hypergraphs（HyperSCI）。简单来说，HyperSCI 控制了混杂因素（confounder），在表征学习（representation learning）的基础上建立了高阶干涉（high-order interference）模型，最后根据学习到的表征做出估计（estimation）。

具体来说，HyperSCI 主要由三部分构成，如图 2 所示，：

（1）Confounder Representation Learning：基于混杂因素（confounder）包含在特征（feature）中的假设，通过表征学习技术，从个体的特征中捕捉和控制混杂因素。

（2）Modeling High-order Interference：通过超图卷积（hypergraph convolution）和注意力机制（attention operation）来学习每个节点的干涉表征（interference representation），从而对干涉（interference）进行建模。

（3）Outcome Prediction：基于学习到的混杂因素表征（confounder representation）和干涉表征（interference representation）来预测个体在不同实验（treatment）下相应的潜在结果（outcome）。

3.1 Confounder Representation Learning

我们先 通过多层感知器（multilayer perceptron MLP）模块将节点特征（feature） 编码到一个隐空间（latent space） ，即 。这样我们就可以得到一组表征（representation） 。 可以捕捉到所有潜在的混杂因素（confounder），所以模型可以通过控制 来减轻混杂偏倚（confounding bias）。我们将 称为混杂因素表征（confounder representation）。

3.1.1 Representation Balancing

由于混杂因素表征 的分布在对照组（control group）和实验组（treatment group）可能存在差异，从而对因果效应估计的结果（causal effect estimation）造成偏差。为了使这种分布的差异最小化，我们决定 在损失函数中加入差异惩罚项（discrepancy penalty）来平衡表征  。 差异惩罚项可以用任何计算两个分布间距离指标来计算。本文采用 Wasserstein-1 distance 作为计算对照组和实验组间表征分布的差异惩罚项。

3.2 Interference Modeling

▲ 图3

在 Interference Modeling 模块，我们把混杂因素表征 、实验分配 （treatment assignment）和超图 上的关系信息（relational information）作为输入，来捕捉个体的高阶干涉（9high-order interference）。具体来说，我们通过超图（hypergraph）来学习一个转换（transformation）函数 来生成每个节点 的干涉表征 （interference representation），即 。

如图 3 所示， 该模块由超图卷积网络（hypergraph convolutional network）和超图注意力机制（hypergraph attention mechanism）构成。 其中，卷积算子形成了超边（hyperedge）干涉的骨架，而注意力算子通过衡量节点对超边（hyperedge）的贡献度来增强这个骨架。

3.2.1 Learning interference representations

为了学习超图（hypergraph）上每个节点的干涉表征（interference representation）， 我们用超图卷积层（hypergraph convolutional layer）来传播实验分配（treatment assignment）和混杂因素表征（confounder representation）。 我们首先为超图 引入一个拉普拉斯矩阵（Laplacian matrix），如公式 1 所示：

▲ 公式1

其中， 是一个对角矩阵， 中的每个元素表示节点的度 。 也是一个对角矩阵， 中的每个元素表示每条超边的大小 。

这样一来，超图卷积算子的定义如公式 2 所示：

▲ 公式2

其中， 代表第 层的表征。我们用经过实验分配后的混杂因素表征 confounder representation 作为干涉表征的第一层，即 ， 表示对应元素相乘（element-wise multiplication）。 是第 层的参数矩阵，其中 和 分别指的是第 层和第 层干涉表征的维度。

3.2.2 Modeling interference with different significance

尽管上述卷积层可以通过超边（hyperedge）传播干涉（interference），但它没有提供太多的灵活性来说明不同节点在不同超边下干涉的意义。在 COVID-19 的例子中，从直觉上来说，那些活跃参加聚会活动的个体更有可能感染或被这些群体中的其他人所传染。因此，为了更好捕捉到超图上节点和超边之间这种内在的关系（intrinsic relationship），我们利用超图注意力机制来学习每个节点及包含该节点的超边的权重（attention weight）。

具体来说，我们给每条超边 计算其表征 。该表征是通过聚合其有关联的节点 得到，即： ，其中 可以是任何聚合函数（aggregation function）。对于每个节点 及其相关的超边 ，节点 和超边 之间的注意力得分的计算如公式 3 所示：

▲ 公式3

其中， 是一个非线性激活函数， 表示与节点 相关的超边集合（the set of hyperedges）。我们用 表示一个用来计算节点-超边间注意力的参数矩阵， 是一个相似度函数，它的实现如公式 4 所示：

▲ 公式4

在公式 4 中， 是一个权重向量（weight vector）， 是一个连结操作（concatenation operation）。

我们用注意力分数（attention score）来模拟不同程度的干涉。具体来说，我们用一个增强矩阵 来取代公式 1 中的原始关联矩阵 ，其中 。这样一来，在同一超边内不同节点的干涉就可以被赋予不同的权重，来表示对建模干涉不同程度的贡献。我们将卷积层最后一层的表征定义为 ，并希望它能捕捉到每个节点的高阶干涉。

3.2.3 Representation Balancing

与 coufounder representation learning 模块类似，我们计算了一个差异惩罚项（discrepancy penalty）来反映干涉表征（interference representation）在对照组和实验组间的分布差异。我们将这两个差异惩罚项相加，计算出一个表征平衡损失 （representation balancing loss）。

3.3 Outcome Prediction

在得到混杂因素表征 和干涉表征 后，我们对潜在结果（potential outcome）进行建模，如公式 5 所示：

▲ 公式5

其中， 和 是可学习的函数，用来预测潜在结果即 和 。在本文中， 和 是两个 。我们通过 得到对观察结果（observed outcome）的预测。我们通过最小化下列损失函数来优化模型，损失函数如公式 6 所示：

▲ 公式6

其中，损失函数的第一项是标准的均方误差（mean squared error）， 是表征平衡损失， 表示这个神经网络模型的参数。 和 是两个超参数，用来控制表征平衡损失和参数正则（parameter regularizatio）项的权重。每个实例 的 ITE 可以被估计为： 。

3.4 Discussion

在这一章节，我们重新审视所提出的 HyperSCI 框架中一些隐含假设。

1. 假设节点 的干涉（interference）是来自其在超图结构上的邻居。这里，来自多跳之外（multiple hops away）邻居的干涉可以通过堆叠更多的超图卷积层来捕获。

2. 为了简单起见，假设每个节点的干涉只来自其他具有非零实验分配（non-zero treatment assignment）的节点；

3. 假设在同一超边（hyperedge）内的节点表征在隐空间（latent space）是相似的；

4. 假设超边表征和节点表征是同质的（homogeneous）。

尽管有上述假设，我们仍然需要提及的是 HyperSCI 是通用的（general）和可扩展的（extendable）。上述假设可以通过丰富超图处理（hypergraph processing） 模块而进一步放宽。

Experiment

实验部分可分为如下章节，关于数据集的处理和介绍在这里不多做赘述，有兴趣的读者可以自行阅读原文。

4.1 Experiment Settings

4.1.1 Metrics

我们通过两个指标来评估因果效应估计（causal effect estimation）的性能，包括异质效应估计（Estimation of Heterogeneous Effect）中的平方根精度 （Rooted Precision） 和平均绝对误差（Mean Absolute Error） 。这两个指标的定义如公式 7 所示：

▲ 公式7

或 越低，表示因果效应估计越好。

4.1.2 Baselines

为了研究 HyperSCI 的有效性，我们有以下三类基线：

1. No graph-LR, CFR, CEVAE

这一类基线不考虑图数据（graph data）和溢出效应（spillover effect）。具体来说，由线性回归 LR 实现的结果（outcome）计算、由反事实回归 CFR (counterfactual regression) 实现的结果预测和因果效应自动编码器 CEVAE (causal effect variational autoencoder)。这一类基线是用来评估建模干涉（modeling interference）对 ITE 估计的有效性。

2. No spillover effect in ordinary graphs - Netdeconf

这一类基线考虑图结构（network structure），但仍不考虑溢出效应（spillover effect）。具体来说，网络去混因子模型 Netdeconf 利用实例间的网络结构 （network structure）来为 ITE 估计捕捉潜在的混杂因子（latent confounder）。

3. Spillover effect in ordinary graphs -

这一类基线可以处理普通图（ordinary graph）上的成对（pairwise）溢出效应 （spillover effect）。它们以一种基于节点表征学习的方法在网络干扰下估计 ITE，分为如下两种：

（1）GNN+HSIC：基于图神经网络（GNNs）和希尔伯特-施密特独立性准则 HSIC（Hilbert Schmidt independence criterion）；

（2） GCN+HSIC ：基于图卷积神经网络（GCN）和希尔伯特-施密特独立性准 HSIC（Hilbert Schmidt independence criterion）。

4.2 ITE Estimation Performance

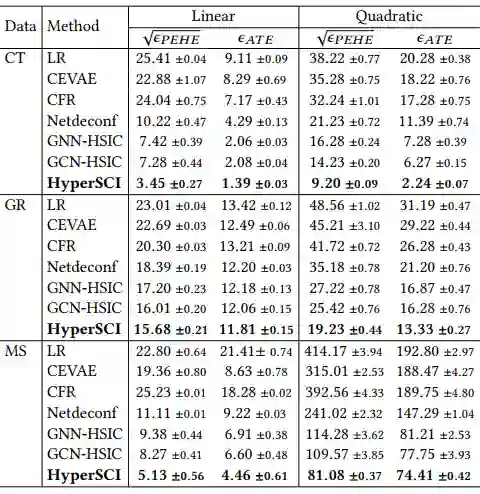
▲ 表1

ITE 估计（ITE estimation）的实验结果如表 1 所示，在线性和二次结果模拟（outcome simulation）的任务下，HyperSCI 表现都优于所有的基线（baseline）。我们认为 HyperSCI 的优越表现源于：它可以利用超图中的关系信息（relational information）来建模高阶干扰（high-order interference），从而减轻了溢出效应（spillover effect）对 ITE 估计任务的负面影响。

此外，与不利用关系信息的基线 LR，CEVAE 和 CFR 相比，利用关系信息的基线，即 NetdeconfGCN-HSIC 和 GNN-HSIC，表现更好。

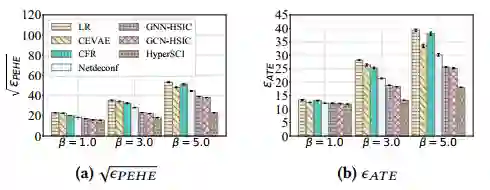
▲ 图4

我们还改变了超参数 来控制超图溢出效应在结果预测（outcome simulation） 中的重要性。实验结果如图4所示，随着 的增加，结果（outcome）受溢出效应的影响越厉害，但所提出的模型 HyperSCI 相对于基线来说仍有很大的性能提升。这一结果进一步验证了我们的框架通过对干扰进行建模来提高 ITE 估计（ITE estimation）的有效性。

4.3 Ablation Study

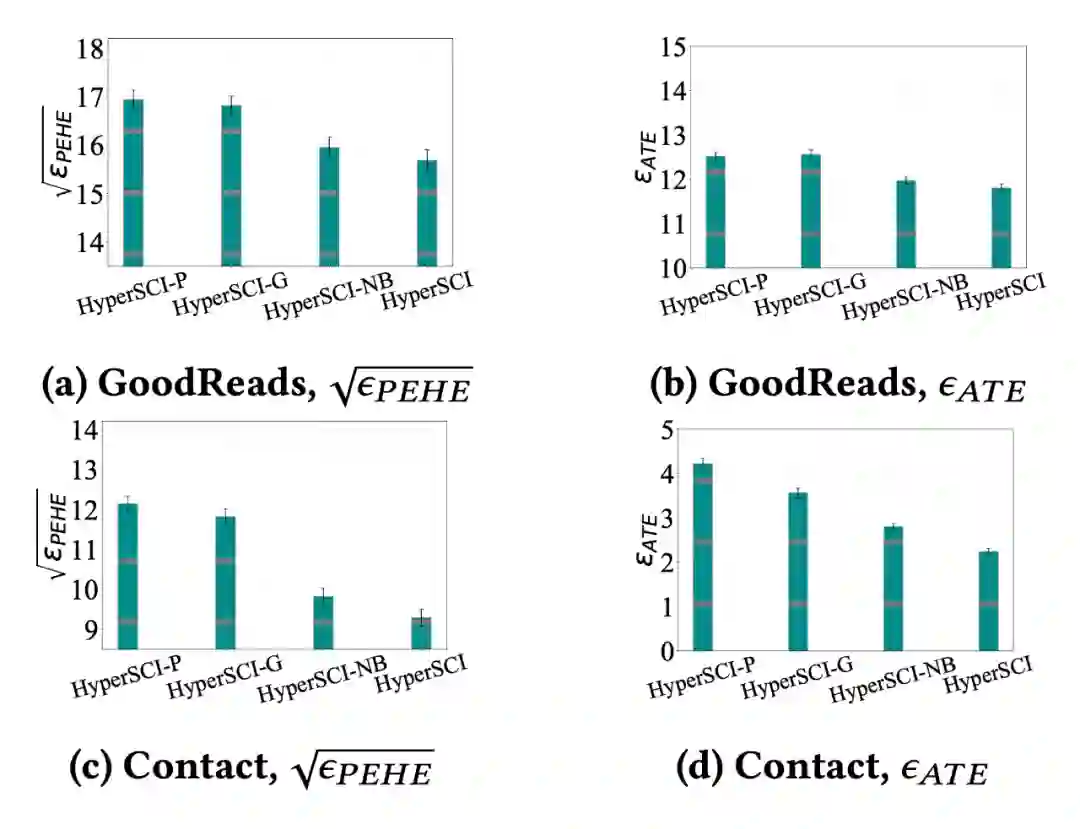
▲ 图5

为了研究 HyperSCI 中不同组成部分的有效性，我们通过以下变种（variant）对进行 HyperSCIL 进行消融实验：

（1）HyperSCI-P：将 HyperSCI 应用于投影图（projected graph）上。请注意该投影图为超图结构（hypergraph structure）。

（2）HyperSCI-G：用一个具有相同层数的图神经网络模块来取代超图神经网络模块，然后将其应用于投影图（以原始图结构的形式）。请注意，尽管 HyperSCI-P 和 HyperSCI-G 都是在投影图上进行评估，但 HyperSCI-G 是用图神经网络模块处理普通图，而 HyperSCI-P 使用超图神经网络模块处理超图。

（3）HyperSCI-NB：移除了 HyperSCI 中的表征平衡模块（balancing technique）。

消融实验的结果如图 5 所示，HyperSCI-P/HyperSCI-G 表现明显差于 HyperSCI。 这证明了对超图上的高阶关系（high-order relationship）进行建模的有效性。 此外，和 HyperSCI 相比，移除了表征平衡模块的 HyperSCI-NB 表现有所下降。 这证明了表征平衡技术在减轻 ITE 估计偏倚（bias）方面的有效性。

4.4 A Closer Look at High-Order Interference

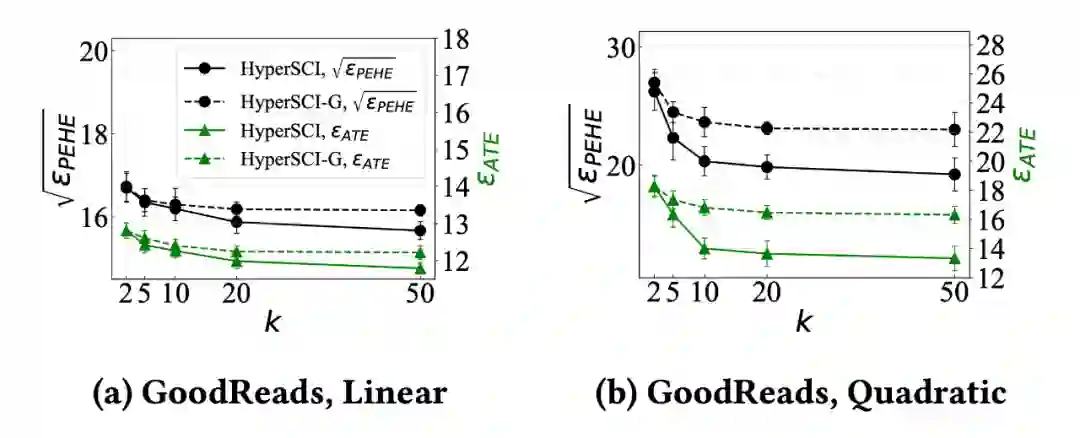
▲ 图6

在这一节中，我们研究了 HyperSCI 是如何应对超边（hyperedge）的不同大小（size）。具体来说，我们移除了尺寸（size）大于 的超边，将修改后的超图表示为 ，并改变 的值。我们比较了 HyperSCI 及其变种 HyperSCI-G 在不同 上的表现。实验结果如图 6 所示，我们有如下发现：

（1） 当 即超边的大小 时，HyperSCI-G 的表现与 HyperSCI 靠近。 这是因为当 时，超图和普通图拉普拉斯矩阵（Laplacian matrix）的差异很小，所以图卷积可以被看作是超图卷积的一个特例。从实验上看，这就导致了 HyperSCIG 和 HyperSCI 之间微小的性能差异。

（2） 当 逐渐增加，HyperSCI 和 HyperSCI-G 的性能都逐渐提高。 但当 增加到一定值之后，两种方法的性能都逐渐稳定。此外，HyperSCI 的表现一直优于 HyperSCI-G，且随着 的增加，两者的表现差异变得更大。这表明 HyperSCI 在建模高阶干扰方面的有效性，尤其是在大的超边上。

4.5 Sensitivity Analysis

▲ 图7

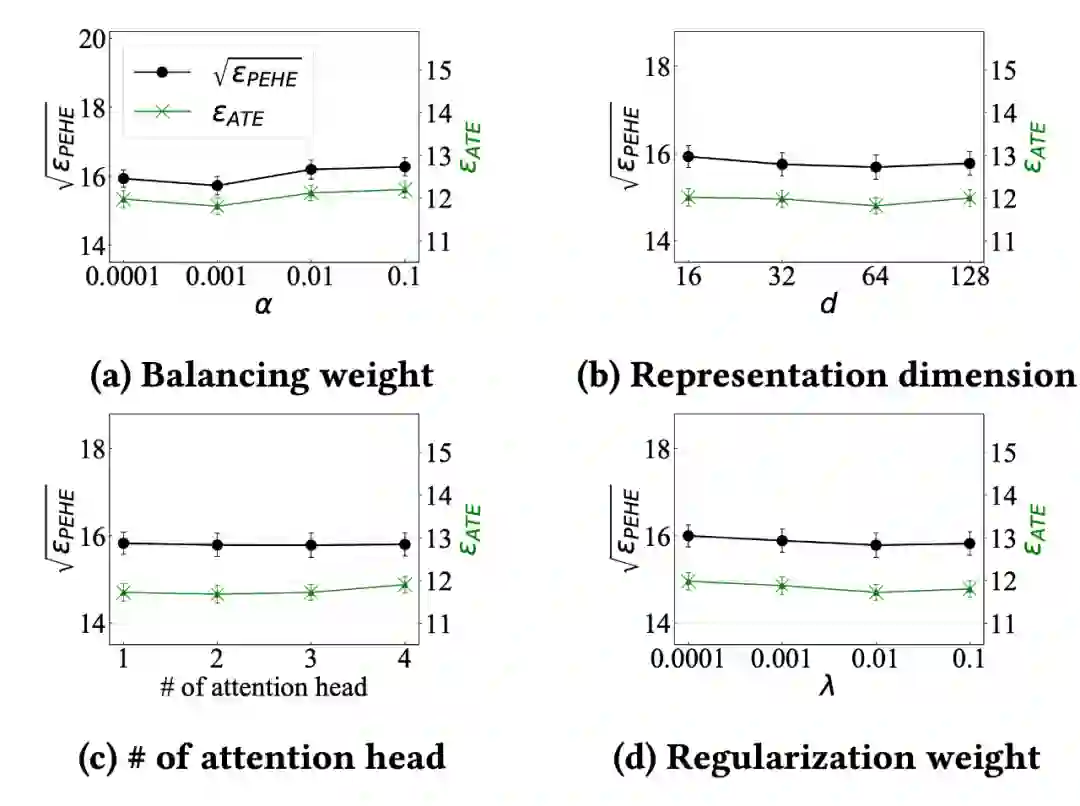
为了评估所提出的框架 HyperSCI 的鲁棒性（robustness），我们在图 7 中展示了 HyperSCI 在不同的超参数设置下的表现。 从实验结果可以看出，HyperSCI 在不同的超参数下总体表现稳健的，但对这些超参数进行适当的微调仍然有利于 HyperSCI 性能。

Conclusion

这篇文章研究了超图上存在高阶干扰（high-order interference）的个体实验效果估计（individual treatment effect estimation）的问题。我们确定并分析了高阶干扰对因果效应（causal effect）估计的影响。为了解决这个问题，我们提出了一个基于表征学习来估计 ITE 的新框架 HyperSCI。

具体来说，HyperSCI 可以学习到混杂因素（confounder）的表征，用超图神经网络模块建立高阶干扰模型，然后用学到的表征预测每个实例的潜在结果（potential outcome）。我们进行了广泛的实验来评估所提出的框架 HyperSCI，结果验证了 HyperSCI 在不同干扰场景下估计 ITE 的有效性。

更多阅读