ICML'22|可解释可泛化的图学习,随机注意力机制就够了!
ICML'22|可解释可泛化的图学习,随机注意力机制就够了!
论文标题: Interpretable and Generalizable Graph Learning via Stochastic Attention Mechanism
作者: Siqi Miao, Mia Liu, Pan Li
论文链接: https://arxiv.org/abs/2201.12987
代码链接: https://github.com/Graph-COM/GSAT
背景
因为图神经网络(GNNs)能够天然的处理不规则的数据结构,如今它们被越来越多的应用在各种科学应用中:比如生物中的蛋白质折叠、材料学中的玻璃动力学模拟、化学中的分子属性预测、高能物理中的Jet Tagging,等等等等。
在这些科学应用中,出色的模型分类性能往往并不是唯一的目标。它们同样重视模型的可解释能力,并希望从训练样本中找出数据的关键特征(Effective Data Patterns)来指导进一步的研究。但是正如其它神经网络一样,GNN本身也无法提供太多的可解释性。因此,人们提出了许多工作来尝试为GNN提供可解释性。
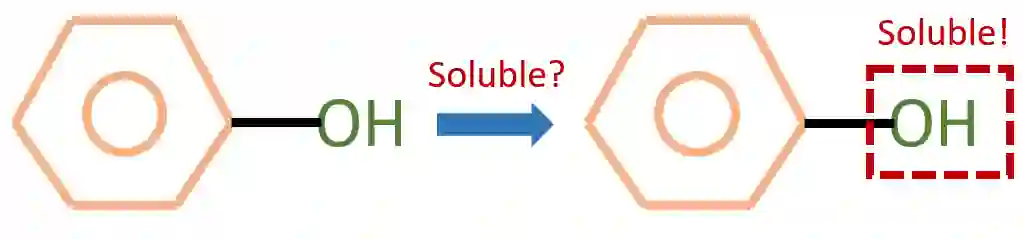
GNN的可解释性问题通常旨在从原始的输入图中提取一个子图:人们希望提取的子图中仅包含最能帮助标签预测的信息。如下图,我们知道-OH官能团能够使得一个分子具有水溶性。因此对于一个用来预测分子水溶性的GNN来说,人们希望给定下图的分子后,模型能够告诉我们对预测最重要的部分是-OH官能团所代表的子图。这样一来,人们就能从模型中获取更多的关于数据关键特征的理解,从而指导进一步的研究。
研究动机
GNN可解释性主要有两大类方法:
-
自身可解释的模型(Inherently Interpretable Models); -
事后解释方法(Post-hoc Interpretation Methods)。
第一类方法主要旨在设计自身即可提供解释性的GNN模型。这类方法往往被人诟病牺牲模型分类性能来换取可解释性。并且这一方向中最常见的设计之一,注意力机制(如GAT),多篇研究显示其无法为GNN带来值得信任的可解释结果。
因此,过去的绝大多数工作均致力于第二类方法,即事后解释方法。这些工作通常假设人们会提供一个预先训练好的GNN。随后它们会将该GNN的参数固定,然后训练一个新的模型,即解释器(Explainer),来从输入图中找出一个子图。它们希望这些子图能够:1)尽可能小;2)尽可能保持原有预测分数。最后这些子图即被认为是GNN捕捉到的数据的关键特征。
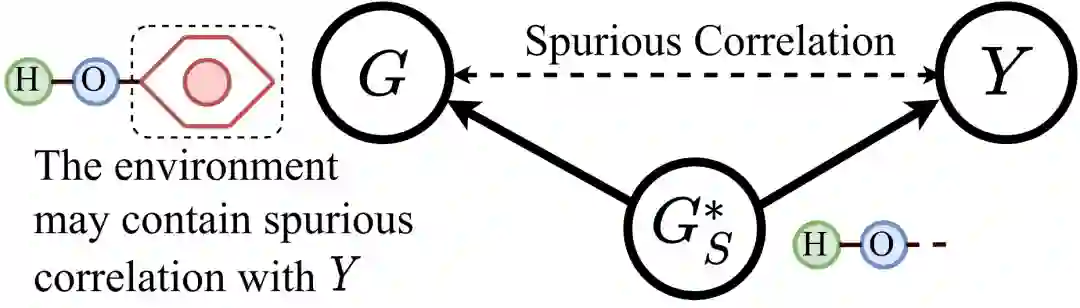
最近,新的基于不变因果特征学习(Invariant Learning)的工作也逐渐被提出。这些工作认为训练数据中可能会存在数据偏见(Data Bias),使得模型最终学习到一些和标签具有伪相关性(Spurious Correlations)的特征。下图展示了伪相关特征的一个例子。这些特征可能是收集或生成训练数据时的偏见造成的,它们实质上并不是真正决定样本类别的特征。而当测试集不存在这些伪相关的特征时,模型的效果将大打折扣。因此,这些工作引入了因果分析理论(Causality Analysis),希望迫使模型学习数据中不变的、与标签具有因果关系的特征(Invariant Causal Patterns),来解决上述OOD 泛化问题(Out-of-distribution Generalization)。这类方法在寻找那些不变的因果特征时,也能提供一定程度的自身可解释性。不过也由于这些方法引入了因果分析,它们的架构往往十分复杂且需要大量的计算。
而在这篇工作中,作者们指出了事后解释方法的诸多问题,并同样专注于设计自身可解释模型。这篇工作提出了一种全新的随机注意力机制(Stochastic Attention Mechanism),该机制显示出了强大的可解释能力和泛化能力。对比过去的可解释工作,该机制在6个数据集上提升了至多20%、平均12%的可解释性能;在11个数据集上提升了平均3%的模型准确率,并且在OGBG-MolHiv榜单上达到SOTA(在不使用手工设计的专家特征的模型中)。
除此之外,该机制对可解释能力和泛化能力的提升同样具有理论保障。在一定假设下,该机制天然的不受伪相关特征的影响,从而能够抓取出真正重要的数据特征。在去除伪相关特征的能力上,该机制以远远更小的复杂度,对比基于因果分析的方法提升了平均12%的OOD泛化能力。
事后解释方法的问题
作者们在文中首先指出了事后可解释方法的四个问题,并认为这些事后解释方法擅长于检查预先训练好的模型对一些特征的敏感程度,但它们并不能提取出对预测真正重要的数据特征,而这才应该是可解释方法需要解决的最有趣的问题。具体来说,作者们指出的四个问题是:
1. 数据分布偏移(Data Distribution Shifts)
首先,事后解释方法将不可避免的遭受数据分布偏移的影响。直觉上,这是因为给定的预先训练好的模型(记作 ),总是在原始输入图 上进行训练的:它从来没有在任何子图 上进行过训练。因而 极有可能在 上是欠拟合的,故而导致 并不能真正反应各个子图 的重要性。
2. 与标签伪相关的数据特征(Spuriously Correlated Patterns)
其次,预先训练得到的 可能会过拟合训练数据中与标签信息伪相关,甚至是无关的特征。这是由于大多数模型本身是基于最大化互信息法则(Maximum Mutual Information Principle)来进行训练的,因此 在训练中自然会捕捉尽可能多的输入特征,而这也是不变因果特征学习这个方向产生的主要动机。
在这种情况下,事后解释方法很可能会将这些伪相关或者无关的特征提取出来,当作数据中的关键特征,而这可能会将人们引入到一个错误的方向。
3. 初始化问题(Initialization Issuses)
随后,作者们从优化和信息瓶颈理论切入,指出事后解释方法对不同的 的初始化是敏感的。在同一个数据集上,基于不同的随机种子训练得到的 ,事后解释方法可能会得出差异较大解释结果。而过去的事后解释方法,在评估时往往会忽略这一点,只基于某一个固定的 ,仅在不同的随机种子上训练解释器。这可能会得到过于乐观的结果,而使得事后解释方法的性能没有得到全面的评估。
4. 潜在的有偏见的约束(Potentially Biased Constraints)
最后,由于上述各种问题,事后解释方法有时很难得出符合人们直觉的解释子图。故而这些方法中往往嵌入稀疏化约束(Sparsity Constraint),或是连接性约束(Connectivity Constraint)等,来得到人们更能理解的数据特征。这些约束极大的要求人们对数据集和任务自身具有一定的先验知识,否则这些约束很可能极大的影响模型的解释结果。一个优秀的可解释模型应当自身即能够抓取适当的数据关键特征而不用附加其它约束。本文提出的随机注意力机制能够在没有上述约束的情况下,取得远远更好的可解释性能。
注:
作者们在论文中提供了更为详细的推理,并通过实验验证了事后解释方法的上述问题。故而作者们认为设计更好的自身可解释模型可能是解决上述问题的关键。感兴趣的读者请进一步阅读该论文原文。
新的注意力机制:图随机注意力 Graph Stochastic Attention (GSAT)
在很长的一段时间里,人们认为注意力机制无法提供较好的可解释性,尤其是在图学习领域。而该论文的作者们提出了一种随机注意力机制,并特别的在图学习领域进行了推导和评估,作者们称该机制为GSAT,即图随机注意力(Graph Stochastic Attention)。后续实验表明该机制能够同时提供强大的可解释能力和泛化能力。
机制原理
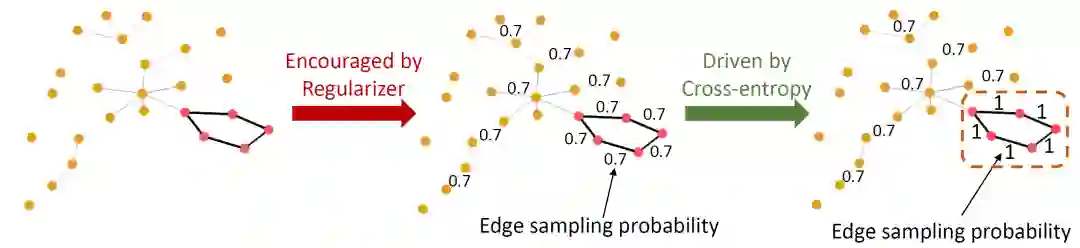
随机注意力机制,顾名思义,即是在学习注意力时注入随机性。下图提供了其在图学习领域的一个例子。该任务目标是预测图中是否存在五节点环(由图中粉色节点包围),这些环中的边是自然则是对预测结果重要的边。该机制原理的直觉如下:
-
首先,每一条边将会习得一个 之间的注意力权重,该权重将指代每一条边在训练中的抽样概率。一个正则项需要被引入来鼓励每一条边习得较小的抽样概率,即维持较大的随机性。如下图中间样本。 -
随后,倘若对预测结果重要的边存在较大的随机性,那么它们在训练中将会被过于频繁的丢弃,而这将极大的影响分类损失(交叉熵)。因此被分类损失推动,重要的边最后则会维持较小的随机性,即习得较大的抽样概率(理想情况下接近于1)。如下图右侧样本。 -
最后,每条边的随机程度指代其对预测性能的重要程度,而越重要的边应有越大的抽样概率。如下图右侧样本虚线框中的子图即为低随机性的子图,它代表着对预测最为重要的子图。
训练目标
现在的问题即是,上述的正则项应当如何选取呢?事实上这也非常直觉。因为作者们的目标是控制训练图中的随机性,而从信息论的角度来说,作者们即是希望控制图中的信息量。那么一个显而易见的选择就是信息瓶颈理论(Information Bottleneck Principle)。通过注入信息瓶颈,GSAT能够天然的控制图中的信息量,从而达到预期的效果。
具体而言,图信息瓶颈损失可以写作:
其中 代表两个随机变量之间的互信息量(Mutual Information), 是一个正则系数,代表信息瓶颈注入的强度。 是一个负责从原图 中提取子图 的模型,而 则是负责对提取出的子图 进行下游任务 的预测的模型。
互信息量自身不易优化,作者们为上述目标中的两项分别推导出了变分上界(Variational Upper Bound)来优化该目标。
-
对于第一项 ,易得其变分上界即为 ,而这事实上就是 基于 进行预测后产生的交叉熵损失。 -
对于第二项中的 ,易得其变分上界为 ,其中 即为 基于 得到的每条边的采样概率;而 即是对各边采样概率分布的一个正则,因为该KL散度本质上将鼓励习得的每条边的采样分布逼近 的分布。举例来说,倘若 是一个参数为 的伯努利分布,那么这一项则将鼓励每条边的采样概率接近 ,而这正好符合作者们对随机注意力机制中正则项工作原理的期待。
有保障的可解释性和OOD泛化(伪相关性去除)能力
由上文可知,最终GSAT的训练目标即是一个分类损失(鼓励高分类性能),加上一个KL散度的正则项(鼓励高随机性)。理想情况下,我们期待当模型仅将重要的边维持较小的随机性时,该训练目标应该被最小化,因为在这种情况下我们可能可以在达到最高分类性能的同时,取得最高的整体随机性。而作者们则在论文的定理4.1中证明了这一点,使得GSAT的性能具有理论保障。
具体来说,论文中定理4.1表明:给定一个任务,如果我们假设输入图 中包含一个子图 ,并且其标签 将由下式决定: ,其中 是一个可逆的且无随机性的函数, 是与 无关的随机噪声。那么对于任何的 能够最小化上文提出的信息瓶颈损失。
这意味着GSAT能够在不利用因果分析工具的情况下,天然的找出真正重要的子图 ,并且移除可能存在的伪相关特征,从而提供有保障的可解释性和OOD泛化能力。
GSAT 模型架构
有了文中提出的两个变分上界,那么GSAT的模型架构问题则变得一目了然。现在只需要对 和 进行适当的参数化。
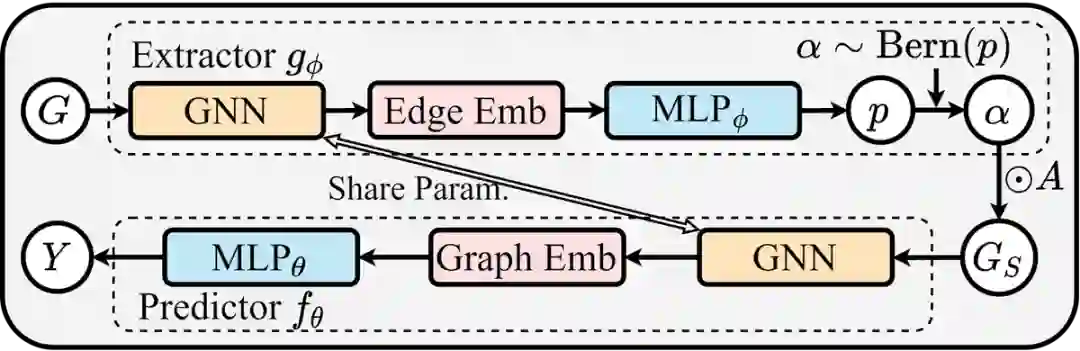
直觉来说,如下图:
-
的输入是原始图 ,其对每一条边输出一个注意力权重,那么 显然可以是一个这样工作的GNN。 -
的输入是子图 ,其输出对该样本的标签预测,那么 显然可以是一个这样工作的GNN。 -
因此,在GSAT中, 将会接受原图 作为输入,然后输出每一条边的随机注意力的值。紧接着,基于随机注意力的取值,一个子图 将会被采样出来。最后 将会被喂给 进行最后的标签预测。 -
尽管 和 可以是两个不同的GNN,但作者们发现这里用同一个GNN效果就足够好。另外,架构中 最后的采样操作本身是不可导的,因此作者们提出利用Gumbel-softmax Trick来重参数化这一步骤,使其可导。
实验
由上一节可见,GSAT架构简单直接,但同时其性能又具有理论保障。这一章节将通过实验结果具体展示GSAT的可解释能力、泛化能力和各模块的消融实验结果。
可解释性
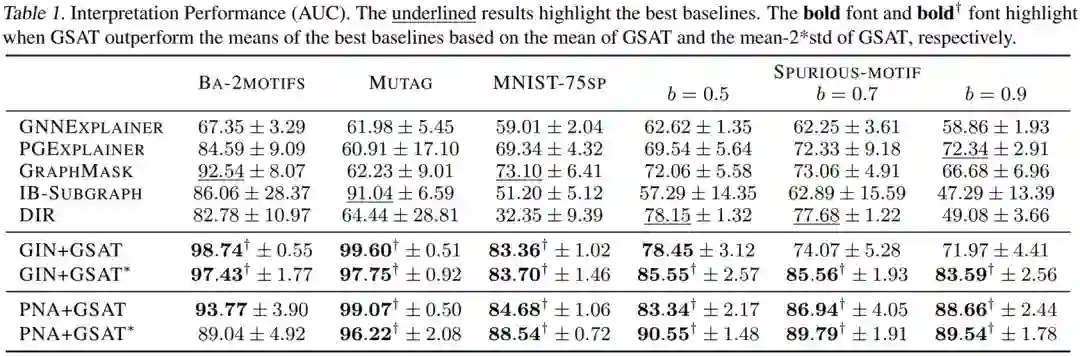
作者们在真实数据集和合成数据集上都对GSAT的可解释性进行了评估。作者们基于这些数据集中已知的解释标注对每个方法的解释结果评估了ROC AUC。如下图,GSAT对比过去的可解释工作,在6个数据集上提升了至多20%、平均12%的可解释性能。
泛化性能
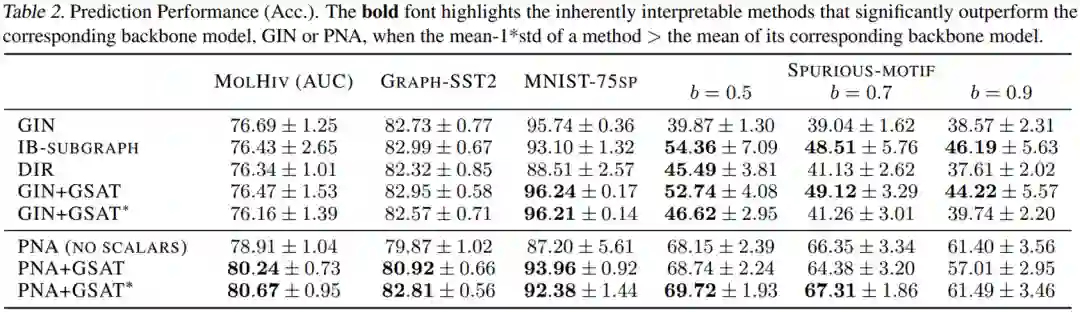
由于GSAT能够帮助去除伪相关性,它同时也能帮助提升模型的分类泛化能力。如下图,GSAT在11个数据集上提升了平均3%的模型准确率,并且在OGBG-MolHiv榜单上达到SOTA(在不使用手工设计的专家特征的模型中)。
OOD泛化性能(伪相关性移除)
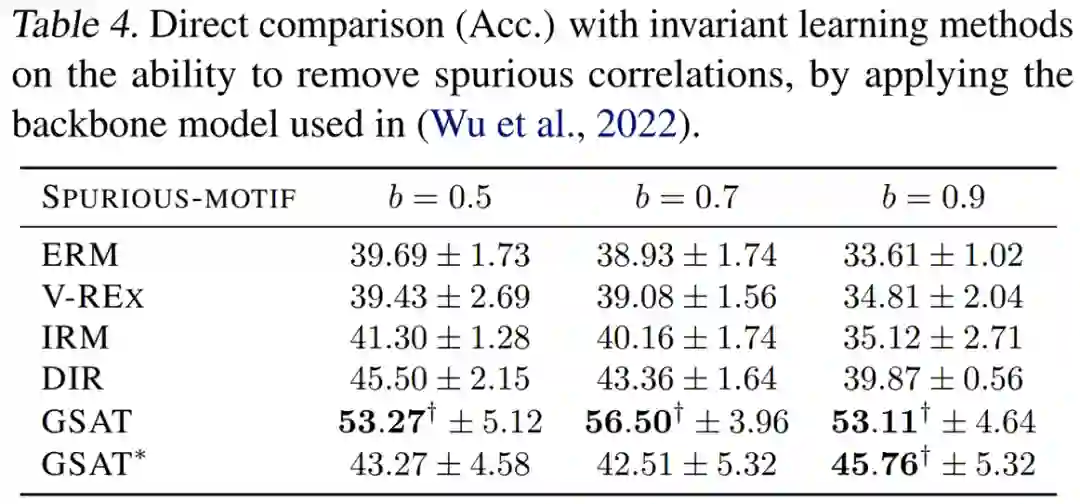
为了对比GSAT的移除伪相关特征的能力,作者们同时提供了和不变因果特征学习的方法的直接对比。如下图,可见GSAT能够在不利用因果分析框架的情况下,以更为简单的架构提升平均12%的OOD泛化能力。
消融实验
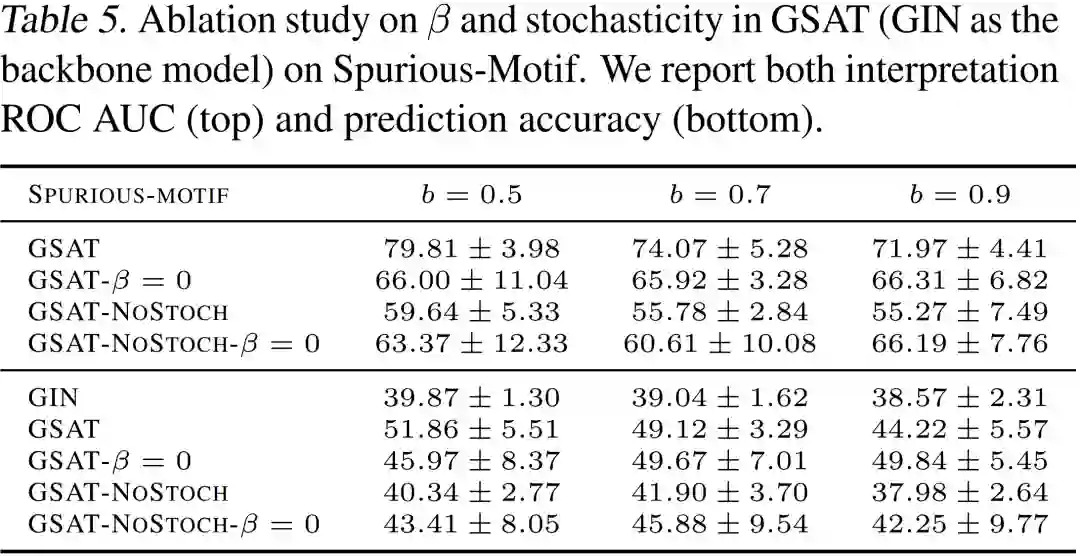
作者们提供了GSAT中各个模块的消融实验结果,如下表,可见当不注入随机性(NoStoch),或者不添加正则项( )时,模型效果均会大幅下降。而当不注入随机性时,模型效果将遭受最大的下降。这一消融实验展示了注入的随机性在GSAT中扮演着极其重要的角色。
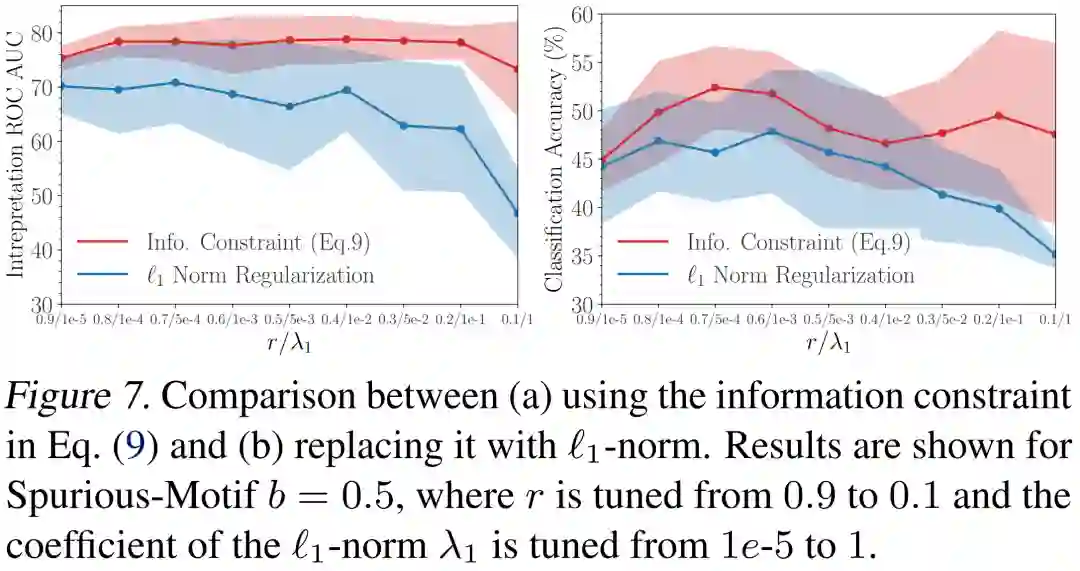
作者们同样实验了将从信息瓶颈中推导得来的KL散度正则项替换成过去的方法常用的
正则。下图对各正则项的系数进行了网格搜索,可见文中提出的信息正则项显著优于
正则。
注:
论文中对各个实验的结果有更多的分析,请有兴趣的读者进一步阅读论文原文。
结论
这篇论文提出了一个全新的图随机注意力机制GSAT,它通过在注意力的学习中注入随机性来达到有保障的可解释能力和泛化能力。这篇论文同时指出了事后解释方法背后潜在的问题,并展示了基于注意力机制的自身可解释模型的巨大潜力。