OpenAI提出Reptile：可扩展的元学习算法

选自OpenAI Blog

作者：ALEX NICHOL & JOHN SCHULMAN

机器之心编译

近日，OpenAI 发布了简单元学习算法 Reptile，该算法对一项任务进行重复采样、执行随机梯度下降、更新初始参数直到习得最终参数。该方法的性能可与 MAML（一种广泛应用的元学习算法）媲美，且比后者更易实现，计算效率更高。

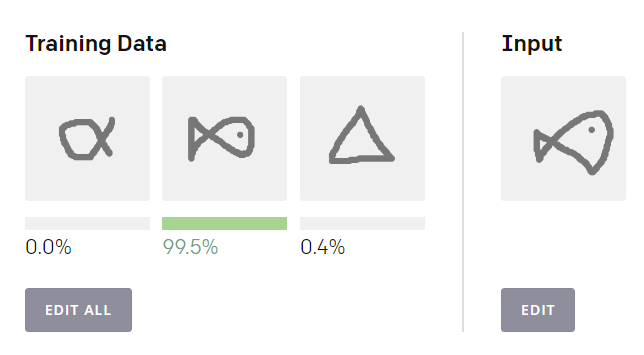
元学习是学习如何学习的过程。元学习算法会学习任务的一个分布，每项任务都是学习问题，并输出快速学习器，学习器可从少量样本中学习并进行泛化。一个得到充分研究的元学习问题是 few-shot 分类，其中每项任务都是分类问题，学习器只能看到 1-5 个输入-输出样本（每个类别），之后学习器必须对新输入进行分类。下面，你可以尝试 OpenAI 的 1-shot 分类交互 Demo，其使用了 Reptile。

点击「Edit All」按钮，绘制三种不同的形状或符号，然后在后侧的输入区域绘制其中一个形状，就可以看到 Reptile 的分类效果。前三个图是标注样本：每个定义一类。最后的图表示未知样本，Reptile 输出其属于每个类别的概率。（请点击原文链接体验交互）

Reptile 的工作原理

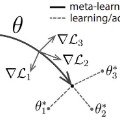
和 MAML 类似，Reptile 会学习神经网络的参数初始化方法，以使神经网络可使用少量新任务数据进行调整。但是 MAML 通过梯度下降算法的计算图来展开微分计算过程，而 Reptile 在每个任务中执行标准形式的随机梯度下降（SGD）：它不用展开计算图或计算任意二阶导数。因此 Reptile 比 MAML 所需的计算量和内存都更少。伪代码如下：

最后一步也可以把 Φ−W 作为梯度，将其插入如 Adam 等更复杂的优化器。

很令人震惊，该方法运行效果很好。如果 k=1，该算法对应「联合训练」（joint training）：在多项任务上执行 SGD。尽管联合训练在很多情况下可以学到有用的初始化，但在 zero-shot 学习不可能出现的情况下（如输出标签是随机排列的）它能学习的很少。Reptile 要求 k>1，更新依赖于损失函数的高阶导数。正如 OpenAI 在论文中展示的那样，k>1 时 Reptile 的行为与 k=1（联合训练）时截然不同。

为了分析 Reptile 的工作原理，OpenAI 使用泰勒级数逼近更新。Reptile 更新最大化同一任务中不同小批量的梯度内积，以改善泛化效果。该发现可能在元学习之外也有影响，如解释 SGD 的泛化性能。OpenAI 的分析结果表明 Reptile 和 MAML 可执行类似的更新，包括具备不同权重的相同两个项。

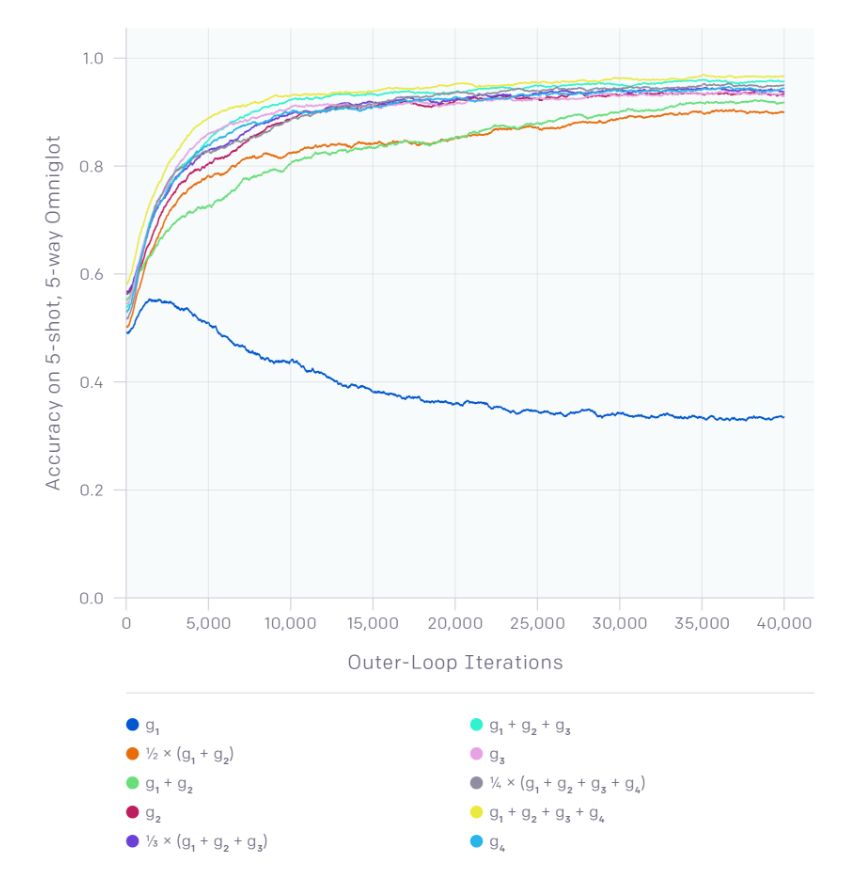
在 OpenAI 的实验中，他们展示了 Reptile 和 MAML 在 Omniglot 和 Mini-ImageNet 基准上执行 few-shot 分类任务时具备类似的性能。Reptile 收敛速度更快，因为其更新具备更低的方差。OpenAI 关于 Reptile 的分析表明，我们可以使用不同的 SGD 梯度组合获取大量不同的算法。在下图中，假设我们在不同任务中使用不同批量大小的 SGD 执行 K 个更新步，产生 g_1,g_2,…,g_k k 个梯度。下图展示了在 Omniglot 上的学习曲线，且它由梯度的和作为元梯度而绘制出。g_2 对应一阶 MAML，即原版 MAML 论文提出的算法。由于方差缩减，使用更多的梯度会导致更快的学习或收敛。注意仅使用 g_1（对应 k=1）如预测那样在这个任务中没有什么提升，因为我们无法改进 zero-shot 的性能。

实现

实现的 GitHub 地址：https://github.com/openai/supervised-reptile

该实现应用 TensorFlow 进行相关的计算，代码可在 Omniglot 和 Mini-ImageNet 上复现。此外，OpenAI 也发布了一个更小的基于 JavaScript 的实现（https://github.com/openai/supervised-reptile/tree/master/web），其对使用 TensorFlow 预训练的模型进行了调整——以上 demo 就是基于此实现的。

最后，下面是一个 few-shot 回归的简单示例，预测 10(x,y) 对的随机正弦波。该示例基于 PyTorch：

import numpy as np
import torch
from torch import nn, autograd as ag
import matplotlib.pyplot as plt
from copy import deepcopy
seed = 0
plot = True
innerstepsize = 0.02 # stepsize in inner SGD
innerepochs = 1 # number of epochs of each inner SGD
outerstepsize0 = 0.1 # stepsize of outer optimization, i.e., meta-optimization
niterations = 30000 # number of outer updates; each iteration we sample one task and update on it
rng = np.random.RandomState(seed)
torch.manual_seed(seed)
# Define task distribution
x_all = np.linspace(-5, 5, 50)[:,None] # All of the x points
ntrain = 10 # Size of training minibatches
def gen_task():
    "Generate classification problem"
    phase = rng.uniform(low=0, high=2*np.pi)
    ampl = rng.uniform(0.1, 5)
    f_randomsine = lambda x : np.sin(x + phase) * ampl
    return f_randomsine
# Define model. Reptile paper uses ReLU, but Tanh gives slightly better results
model = nn.Sequential(
    nn.Linear(1, 64),
    nn.Tanh(),
    nn.Linear(64, 64),
    nn.Tanh(),
    nn.Linear(64, 1),
)
def totorch(x):
    return ag.Variable(torch.Tensor(x))
def train_on_batch(x, y):
    x = totorch(x)
    y = totorch(y)
    model.zero_grad()
    ypred = model(x)
    loss = (ypred - y).pow(2).mean()
    loss.backward()
    for param in model.parameters():
        param.data -= innerstepsize * param.grad.data
def predict(x):
    x = totorch(x)
    return model(x).data.numpy()
# Choose a fixed task and minibatch for visualization
f_plot = gen_task()
xtrain_plot = x_all[rng.choice(len(x_all), size=ntrain)]
# Reptile training loop
for iteration in range(niterations):
    weights_before = deepcopy(model.state_dict())
    # Generate task
    f = gen_task()
    y_all = f(x_all)
    # Do SGD on this task
    inds = rng.permutation(len(x_all))
    for _ in range(innerepochs):
        for start in range(0, len(x_all), ntrain):
            mbinds = inds[start:start+ntrain]
            train_on_batch(x_all[mbinds], y_all[mbinds])
    # Interpolate between current weights and trained weights from this task
    # I.e. (weights_before - weights_after) is the meta-gradient
    weights_after = model.state_dict()
    outerstepsize = outerstepsize0 * (1 - iteration / niterations) # linear schedule
    model.load_state_dict({name : 
        weights_before[name] + (weights_after[name] - weights_before[name]) * outerstepsize 
        for name in weights_before})
    # Periodically plot the results on a particular task and minibatch
    if plot and iteration==0 or (iteration+1) % 1000 == 0:
        plt.cla()
        f = f_plot
        weights_before = deepcopy(model.state_dict()) # save snapshot before evaluation
        plt.plot(x_all, predict(x_all), label="pred after 0", color=(0,0,1))
        for inneriter in range(32):
            train_on_batch(xtrain_plot, f(xtrain_plot))
            if (inneriter+1) % 8 == 0:
                frac = (inneriter+1) / 32
                plt.plot(x_all, predict(x_all), label="pred after %i"%(inneriter+1), color=(frac, 0, 1-frac))
        plt.plot(x_all, f(x_all), label="true", color=(0,1,0))
        lossval = np.square(predict(x_all) - f(x_all)).mean()
        plt.plot(xtrain_plot, f(xtrain_plot), "x", label="train", color="k")
        plt.ylim(-4,4)
        plt.legend(loc="lower right")
        plt.pause(0.01)
        model.load_state_dict(weights_before) # restore from snapshot
        print(f"-----------------------------")
        print(f"iteration               {iteration+1}")
        print(f"loss on plotted curve   {lossval:.3f}") # would be better to average loss ove

论文：Reptile: a Scalable Metalearning Algorithm 

地址：https://d4mucfpksywv.cloudfront.net/research-covers/reptile/reptile_update.pdf

摘要：本论文讨论了元学习问题，即存在任务的一个分布，我们希望找到能在该分布所采样的任务（模型未见过的任务）中快速学习的智能体。我们提出了一种简单元学习算法 Reptile，它会学习一种能在新任务中快速精调的参数初始化方法。Reptile 会重复采样一个任务，并在该任务上执行训练，且将初始化朝该任务的已训练权重方向移动。Reptile 不像同样学习初始化的 MAML，它并不要求在优化过程中是可微的，因此它更适合于需要很多更新步的优化问题。我们的研究发现，Reptile 在一些有具备完整基准的 few-shot 分类任务上表现良好。此外，我们还提供了一些理论性分析，以帮助理解 Reptile 的工作原理。

原文链接：https://blog.openai.com/reptile/

点击下方“阅读原文”了解更多信息

↓↓↓