学界 | 一个样本也能准确学习，OpenAI元学习算法邀你体验

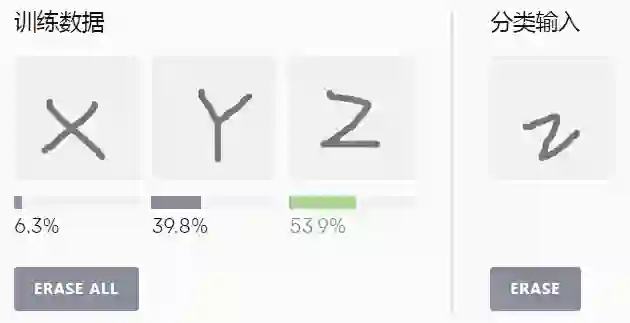
 AI 科技评论按：OpenAI 今天发表了一篇博客介绍了自己新设计的元学习算法「Reptile」。算法的结构简单，但却可以同时兼顾单个样本和大规模样本的精确学习。OpenAI 甚至还在博客页面上做了一个互动界面，可以直接在四个方框里画出训练样本和要分类的样本，算法可以立即学习、实时更新分类结果。

用 Reptile 实时小样本学习，分类手绘图案。训练数据和要分类的图案都可以任意绘制。欢迎到博客页面 https://blog.openai.com/reptile/ 自行尝试一下。

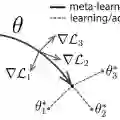
根据 OpenAI 的介绍，这个新的元学习（meta-learning）算法 Reptile 的运作原理是反复对任务采样、在其上运用梯度下降，并从初始参数开始持续地向着任务上学到的参数更新。Reptile 可以和应用广泛的元学习算法 MAML （model-agnostic meta-learning）达到同样的表现，同时还更易于实现、计算效率更高。AI 科技评论把这篇介绍博客全文翻译如下。

元学习是一个学习「如何学习」的过程。一个元学习算法要面对一组任务，其中每一个任务都是一个学习问题；然后算法会产生一个快速学习器，这个学习器有能力从很小数目的一组样本中泛化。小样本分类（few-shot classification）就是一个得到了充分研究的元学习问题，其中的每个任务都是一个分类问题，这里的学习器只能看到每个类别的 1 个到 5 个输入-输出样本，然后它就要开始对新的输入样本进行分类。

Reptile 的工作方式

和 MAML 类似，Reptile 首先会为神经网络寻找一组初始参数，以便网络稍后可以根据来自新任务的数量不多的几个样本进行精细调节（fine-tune）。不过，相比于 MAML 需要在梯度下降算法的计算图中展开并求导，Reptile 只需要简单地在每个任务中以标准方法执行随机梯度下降（SGD），并不需要展开一个计算图以及计算任何二阶导数。这样的设计让 Reptile 所需的计算资源和存储资源都比 MAML 更小。Reptile 的伪码如下所示：

这里的最后一步也有另一种做法，可以把 Φ−W 整体作为梯度，然后把它嵌入进 Adam 之类的更复杂的优化器中。

OpenAI 的研究人员们从一开始就感到惊讶，惊讶的是这个算法居然能运行出结果。当 k =1 的时候，这个算法就相当于是「联合训练」，在所有任务的混合体中做随机梯度下降。虽然联合训练在某些状况下可以作为一种有用的初始化手段，但是零样本学习（zero-shot learning）不可用的时候（比如当输出标签被随机替换了），它所能学到的东西就非常有限。Reptile 算法中需要 k >1，也就是说，参数更新依靠的是损失函数的更高阶导数。正如论文中所示的，此时算法的表现和 k =1 时相比有很大不同。

为了分析为什么 Reptile 会奏效，OpenAI 的研究人员们用泰勒级数逼近了参数更新。他们发现 Reptile 的更新可以让在同一个任务中不同 minibatch 的梯度的内积最大化，这就对应了模型的更强的泛化能力。这一发现也有超出了元学习研究领域的指导意义，可能可以用来解释随机梯度下降的泛化性质。OpenAI 的研究表明 Reptile 和 MAML 执行的参数更新非常详细，包括其中有两个相同的项，不过权重不一样。

在 OpenAI 的实验中，Reptile 和 MAML 在 Omniglot 和 Mini-ImageNet 的两项小样本学习 benchmark 中取得了近似的表现。Reptile 收敛到最终解决方案的速度也更快，因为它的更新的方差更小。

OpenAI 对 Reptile 的分析也表明，通过对随机梯度下降的梯度做不同的组合，我们可以得到许多中不同的算法。假设每个任务中使用不同的 minibatch 进行 k 步随机梯度下降，得到的梯度分别为 g1、g2、……、gk。下图就展示了在 Omniglot benchmark 中把每种不同的梯度和作为元学习的梯度的算法的学习曲线。g2 对应的是一阶 MAML，也就是最初的 MAML 论文中表述的算法。包括的梯度越多，算法学习得就越快，因为其中的方差会随之减小。可以注意到仅仅使用 g1（也就是 k =1 时）并不会给这个任务带来什么改进，因为零样本学习无法被改进。

算法实现

OpenAI 已经把 Reptile 的算法实现开源在了 GitHub 上。它的计算借助 TensorFlow 完成，而且开源中也包括了复现 Omniglot 和 Mini-ImageNet 的两项小样本学习 benchmark 的代码。他们也编写了一个 JavaScript 的实现，模型预训练仍然由 TensorFlow 完成，然后 JavaScript 根据样本做精细调节。OpenAI 博客中的算法样例（也就是本文的开头动图）就是借助  JavaScript 实现完成的。PyTorch 实现的完整代码也一并在博客页面上给出。

论文地址：

https://d4mucfpksywv.cloudfront.net/research-covers/reptile/reptile_update.pdf 

开源地址：

https://github.com/openai/supervised-reptile 

via OpenAI Blog，AI 科技评论编译。

—————  AI 科技评论招人了  —————

—————  给爱学习的你的福利  —————

三大模块，五大应用，手把手快速入门NLP

海外博士讲师，丰富项目经验

算法+实践，搭配典型行业应用

随到随学，专业社群，讲师在线答疑

点击阅读原文或扫码了解详情

▼▼▼

————————————————————