OpenAI邀您体验元学习算法Reptile，一个样本也能准确学习

本文转载自AI科技评论

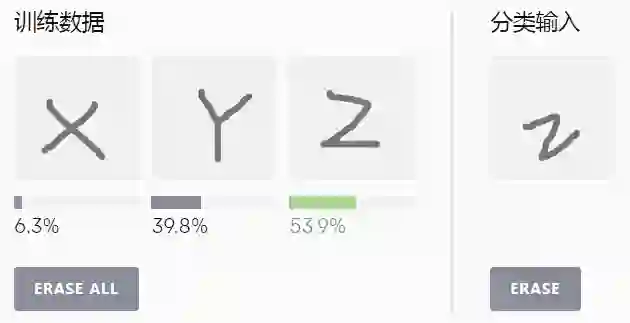
日前，OpenAI发表了一篇博客介绍了自己新设计的元学习算法「Reptile」。算法的结构简单，但却可以同时兼顾单个样本和大规模样本的精确学习。OpenAI甚至还在博客页面上做了一个互动界面，可以直接在四个方框里画出训练样本和要分类的样本，算法可以立即学习、实时更新分类结果。

用Reptile实时小样本学习，分类手绘图案。训练数据和要分类的图案都可以任意绘制。欢迎到博客页面https://blog.openai.com/reptile/自行尝试一下。

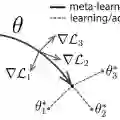
根据OpenAI的介绍，这个新的元学习（meta-learning）算法Reptile的运作原理是反复对任务采样、在其上运用梯度下降，并从初始参数开始持续地向着任务上学到的参数更新。Reptile可以和应用广泛的元学习算法MAML（model-agnostic meta-learning）达到同样的表现，同时还更易于实现、计算效率更高。

元学习是一个学习「如何学习」的过程。一个元学习算法要面对一组任务，其中每一个任务都是一个学习问题；然后算法会产生一个快速学习器，这个学习器有能力从很小数目的一组样本中泛化。小样本分类（few-shot classification）就是一个得到了充分研究的元学习问题，其中的每个任务都是一个分类问题，这里的学习器只能看到每个类别的1个到5个输入-输出样本，然后它就要开始对新的输入样本进行分类。

Reptile的工作方式

和MAML类似，Reptile首先会为神经网络寻找一组初始参数，以便网络稍后可以根据来自新任务的数量不多的几个样本进行精细调节（fine-tune）。不过，相比于MAML需要在梯度下降算法的计算图中展开并求导，Reptile只需要简单地在每个任务中以标准方法执行随机梯度下降（SGD），并不需要展开一个计算图以及计算任何二阶导数。这样的设计让Reptile所需的计算资源和存储资源都比MAML更小。Reptile的伪码如下所示：

这里的最后一步也有另一种做法，可以把Φ−W整体作为梯度，然后把它嵌入进Adam之类的更复杂的优化器中。

OpenAI的研究人员们从一开始就感到惊讶，惊讶的是这个算法居然能运行出结果。当k=1的时候，这个算法就相当于是「联合训练」，在所有任务的混合体中做随机梯度下降。虽然联合训练在某些状况下可以作为一种有用的初始化手段，但是零样本学习（zero-shot learning）不可用的时候（比如当输出标签被随机替换了），它所能学到的东西就非常有限。Reptile 算法中需要k>1，也就是说，参数更新依靠的是损失函数的更高阶导数。正如论文中所示的，此时算法的表现和k=1时相比有很大不同。

为了分析为什么Reptile会奏效，OpenAI的研究人员们用泰勒级数逼近了参数更新。他们发现Reptile的更新可以让在同一个任务中不同minibatch的梯度的内积最大化，这就对应了模型的更强的泛化能力。这一发现也有超出了元学习研究领域的指导意义，可能可以用来解释随机梯度下降的泛化性质。OpenAI的研究表明Reptile和MAML执行的参数更新非常详细，包括其中有两个相同的项，不过权重不一样。

在OpenAI的实验中，Reptile和MAML在Omniglot和Mini-ImageNet的两项小样本学习benchmark中取得了近似的表现。Reptile收敛到最终解决方案的速度也更快，因为它的更新的方差更小。

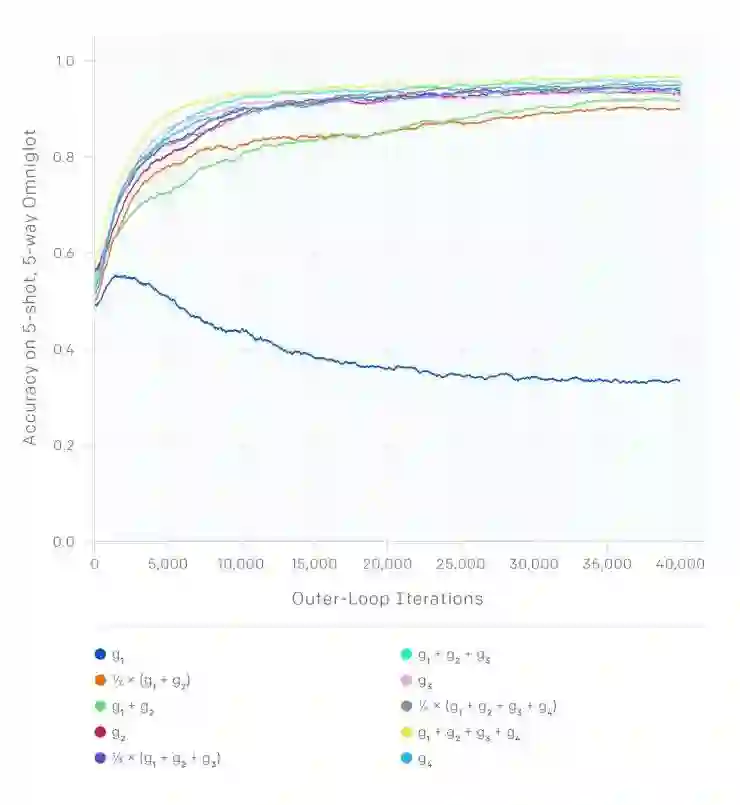
OpenAI对Reptile的分析也表明，通过对随机梯度下降的梯度做不同的组合，我们可以得到许多中不同的算法。假设每个任务中使用不同的minibatch进行k步随机梯度下降，得到的梯度分别为g1、g2、……、gk。下图就展示了在Omniglot benchmark中把每种不同的梯度和作为元学习的梯度的算法的学习曲线。g2对应的是一阶MAML，也就是最初的MAML论文中表述的算法。包括的梯度越多，算法学习得就越快，因为其中的方差会随之减小。可以注意到仅仅使用g1（也就是k=1时）并不会给这个任务带来什么改进，因为零样本学习无法被改进。

算法实现

OpenAI已经把Reptile的算法实现开源在了GitHub上。它的计算借助TensorFlow完成，而且开源中也包括了复现Omniglot和Mini-ImageNet的两项小样本学习benchmark的代码。他们也编写了一个JavaScript的实现，模型预训练仍然由TensorFlow完成，然后JavaScript根据样本做精细调节。OpenAI博客中的算法样例（也就是本文的开头动图）就是借助  JavaScript实现完成的PyTorch实现的完整代码也一并在博客页面上给出。

论文地址：

https://d4mucfpksywv.cloudfront.net/research-covers/reptile/reptile_update.pdf 

开源地址：

https://github.com/openai/supervised-reptile 

📚往期文章推荐

人工智能名人堂第49期 | 斯坦福研究院名人堂成员：Peter E. HaAI+区块链丨区块链如何解锁人工智能新领域

🔗生于伽利略祭日，卒于爱因斯坦诞辰丨巨星陨落，纪念霍金

🔗活动通知丨中国自动化学会第4期智能自动化学科前沿讲习班暨第14期自动化前沿热点论坛

🔗两会速递丨科技部部长万钢：发展AI要从“快”到“强”

🔗两会速递丨杨善林院士：建议深化改革“杰青”“长江学者”管理

🔗人们更偏爱假消息？《科学》发文探讨假消息的科学

🔗李飞飞纽约时报最新博文：如何让AI更好地关怀人类

🔗他物理曾考39分，拼搏不息终成清华物理大师

🔗物理学家辞掉NASA工作玩折纸，专注折纸把卫星送上了天

🔗“女神”传奇：中国最早四位女留学生的故事

🔗她是Sci-Hub背后的“盗版女王”，被出版机构视为死敌的“侠盗”

德先生公众号 ｜ 往期精选

在公众号会话位置回复以下关键词，查看德先生往期文章！

人工智能｜机器崛起｜区块链｜名人堂

虚拟现实｜无人驾驶｜智能制造｜无人机

科研创新｜网络安全｜数据时代｜人机大战

……

更多精彩文章正在赶来，敬请期待！

点击“阅读原文”，移步求知书店，可查阅选购德先生推荐书籍。