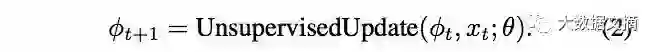论文Express | 谷歌大脑:基于元学习的无监督学习更新规则
大数据文摘作品
编译:杨小咩是小怪兽、晓莉 、小鱼
这期论文Express,让文摘菌带大家来看看谷歌大脑和伯克利关于无监督学习的联合研究。
大数据文摘后台对话框内回复“元学习”即可下载论文~
无监督学习的一个主要目的是为了获得对后续任务有用的数据分布,从而避免在有监督训练过程中需要对数据进行标注的繁琐步骤。
通常,这个目标是通过定义一个代价函数(Cost Function)来最小化估计参数的方式实现的,例如negative log-likelihood(NLL)生成模型。
论文作者:Luke Metz、Niru Maheswaranathan、Brian Cheung、Jascha Sohl-Dickstein(谷歌大脑/加州大学伯克利分校)
本文提出了基于元学习的无监督学习更新规则,利用元学习技术对无监督权重的更新规则进行学习,在针对小样本分类任务上表现良好。
此外,我们将无监督学习更新规则约束为一个生物机制的局部神经元函数,从而推演一种全新的神经网络结构。
基于元学习的无监督学习更新规则可概括为训练不同宽度,深度和非线性的网络。它还可以训练具有随机排列输入维度的数据,甚至还可以从相对复杂的图像数据集泛化到一个文本任务。
相关工作
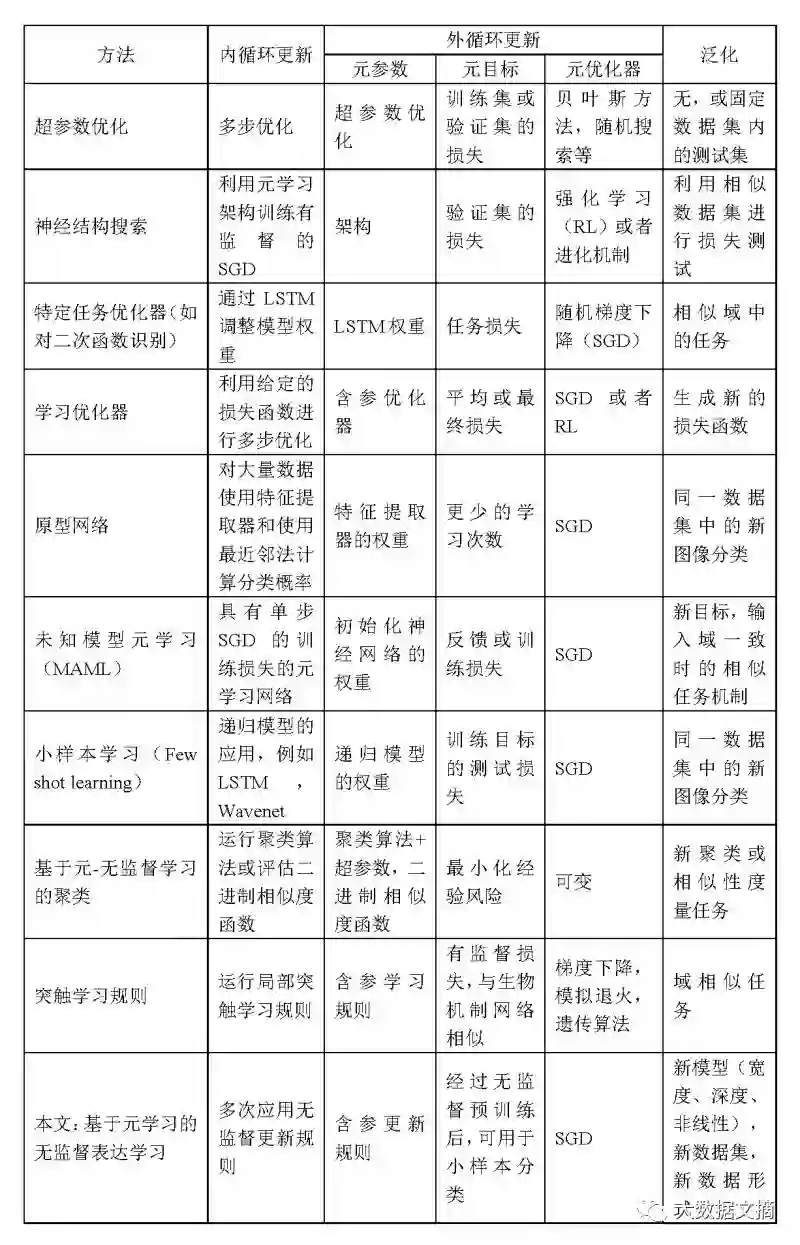
下表中列出了已经在论文中发表的元学习方法,从选择不同的任务类型、元学习结构、元架构和域等方面进行了全面的比较。
已发表的元学习方法比较
模型设计
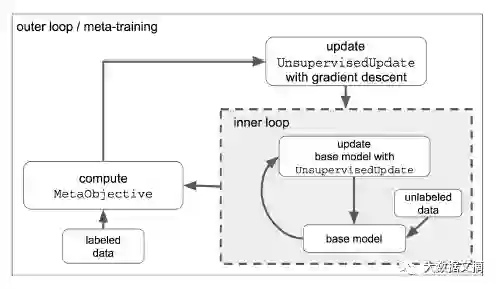
我们将参数为∅t的多层感知机(MLP)f(·; ∅t)作为基础模型,元学习过程的内部循环通过迭代应用学习优化器来训练模型,下图是模型结构示意。
模型结构
在标准的监督学习中,“学习”优化过程就是随机梯度下降(SGD)。有监督损失函数l (x, y)与这个模型相关,其中x是小样本输入,y是相对应的标签。通过使用梯度∂l(x,y)/ ∂φ_t执行SGD,迭代更新基础模型的参数φ_t至收敛。有监督更新规则可以被写成:
其中θ是优化器的参数(例如学习速率),我们称其为元参数(通常也叫做超参数)。
本文中的学习优化器是一个参数更新过程,它并不依赖于标签信息,
在传统的无监督学习算法中,专家知识或者一个简单的超参数搜索决定了θ,其中包括一些元参数,例如学习率和正则化常数。相比之下,我们的更新规则有更多数量级的元参数,例如神经网络的权重。我们在元目标上执行SGD来训练这些元参数,以便找到最佳参数θ∗,将一组训练任务的元目标最小化。
训练更新规则
近似梯度训练
考虑到θ的高维性质,本文通过截断BP算法评估∂[MetaObjective]/ ∂θ对参数θ进行优化,采样每次截断的步数和无监督训练步数的总数以限制由截断引入的潜在偏差。
梯度稳定训练
限制最大内环步长对于优化器的稳定性至关重要。如果不限制学习率,优化器的学习速度会迅速提高并进入混沌区域。
当使用学习优化器时,特别是在学习优化器的元训练的初期,学习优化器很容易在基础模型中产生高方差权重,批标准化(Batch Norm)通过增加权重空间可以解决上述问题。
元训练的分布与泛化
本文中学习优化器的泛化来自于无监督更新(UnsupervisedUpdate)的形式和元训练分布。此外对数据集和基础模型架构上的分布也进行了训练。
本文构建了一套由CIFAR10、来自ImageNet的子集的多类识别和一个由渲染字体组成的数据集组成的训练任务。
我们发现增加训练数据集的变化有助于优化过程。为了减少计算量,我们将输入数据大小限制为小于16x16像素,并相应地调整所有数据集的大小。
在预处理中,我们根据特征维度对所有输入进行转置,以便无监督更新能够学习到一个置换不变性学习规则。
为了增加数据集的变化,我们还通过移位,旋转和噪声来扩大数据集,并将这些增强系数作为元目标的附加回归目标,例如旋转图像并预测旋转角度以及图像类别。
实验结果
本文研究了现有的无监督学习和元学习方法的局限性,然后展示了我们提出的学习优化器的元训练(meta-training)和泛化特性,最后对学习优化器的运行原理进行说明。
目标函数失配
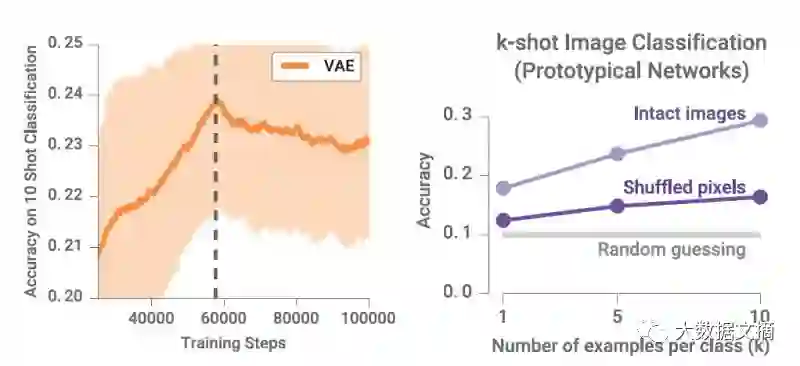
尽管变分自编码器(variational auto-encoder,VAE)分类准确率在一定范围内会随着训练步数的增加而提高,但在训练后期,其分类准确率会所下降。这种结果是由于目标函数失配引起的,例如下图中小样本分类结果。
半监督学习算法的失效模式
上图中,左图是目标函数失配曲线。右图是原型网络在随机输入下的分类准确率。
元优化(Meta-Optimization)
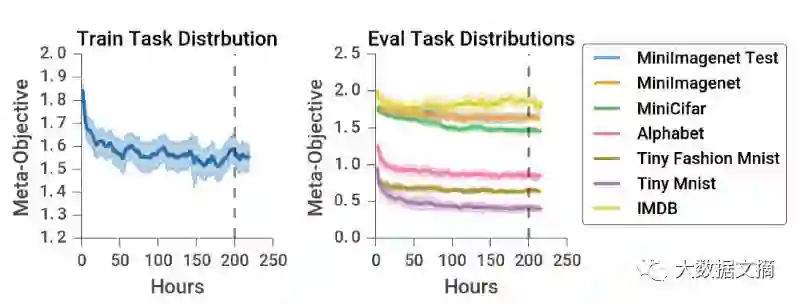
在训练过程中,通过平均所有数据集、模型结构和算法展开执行步骤,监测了元目标(meta-objective)的移动平均数,如下图所示。
训练和评估任务分布的训练曲线
上图中,经过200小时的训练后,训练损失在不断下降,表明近似的训练算法都可以进行有效的学习。为了获得全局参数,我们在多种训练集和测试集上运行了学习优化器,如右图所示。其中,像imagenet、MNIST和Fashion Mnist等数据集的评估损失都有所下降。在训练像IMDB等数据集,就出现了过拟合现象。因此,在200小时后的元训练中,我们用元参数θ进行无监督更新。
泛化
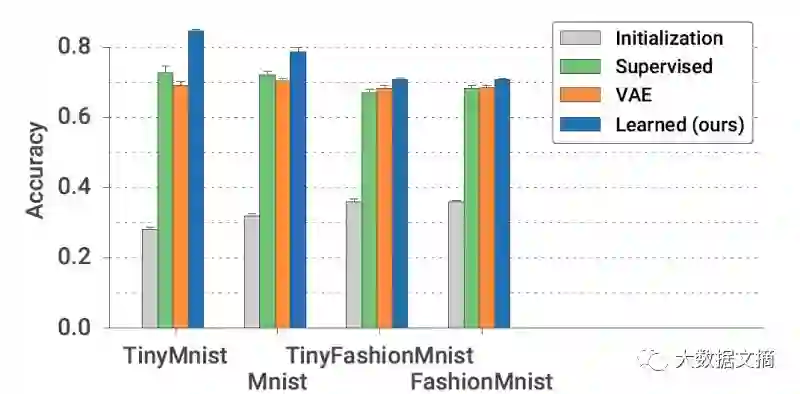
我们最先泛化的对象就是数据集。在下图中,通过在学习模型中嵌入了针对像素的后验分布的变分自编码器,并通过有监督学习比较了小样本分类(每一类有10个样本)的性能,如下图所示。
学习优化器泛化到不可见的数据集
上图中,在同一标签数据集上,我们学习的更新规则产生的表达能力比随机初始化或变分自编码器的输出结果更适合小样本分类。
为了进一步探索优化器的泛化能力,我们利用二进制文本分类数据集:IMDB电影评论,训练了学习优化器,该数据集通过计算一个包含1000个单词的词袋进行编码。
我们分别使用训练了30个小时和200个小时的模型来评估元训练的效果。尽管只利用了图像数据进行训练,训练了30个小时的学习优化器比随机初始化的识别准确率提高了近10%。
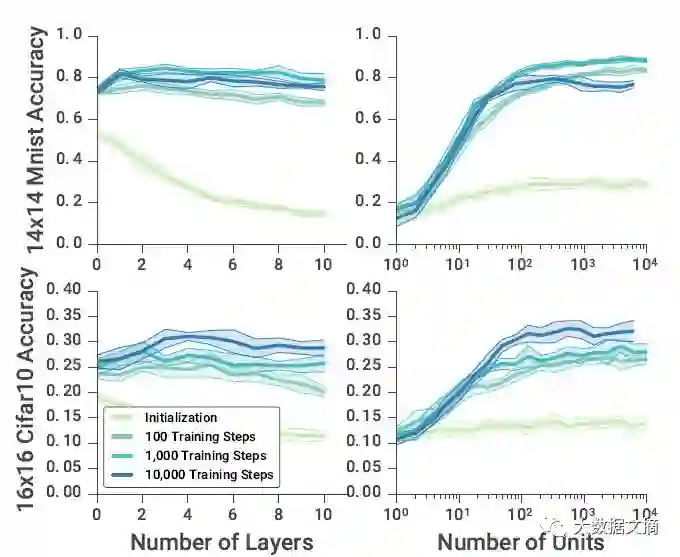
我们要泛化下一个的属性是神经网络结构。我们使用学习优化器训练不同深度和单位计数的模型,并比较了在不同时间点的结果,如下图所示。结果表明,尽管只训练了2-5层的网络和每层64-512个单元,学习规则可泛化到11层,每层10000个单元。
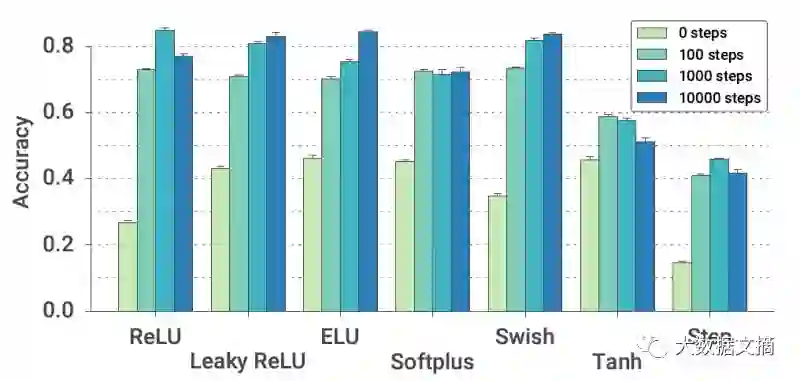
接下来我们将考察模型在不同激活函数上的泛化。我们将学习优化器应用于具有多种不同激活功能的基础模型上。在训练过程中不同点上的性能评估可以在下图中看到。
尽管训练中只使用了ReLU激活函数,但我们的学习优化器在所有情况下的表现都优于随机初始化。
探索学习优化器的学习过程
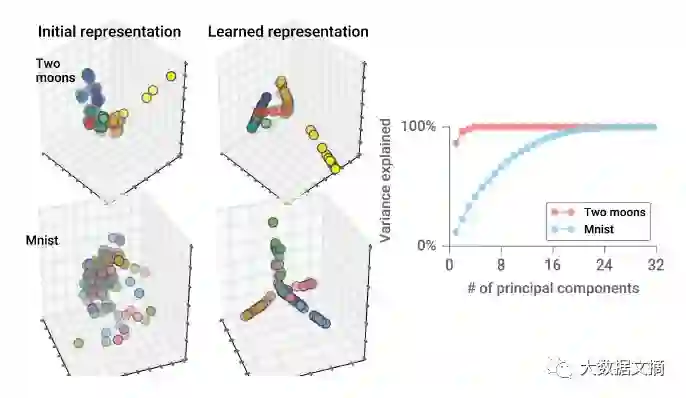
为了理解算法的学习过程,我们在学习优化器中输入了两个moon数据集。尽管是二维数据集,与元训练中使用的图像数据集不同,但学习模型仍然能够识别出以一种完全无监督的方式生成的数据集,如下图所示。
上图是经过学习优化器分类后的可视化结果。输入数据集分别为moon和MNIST,学习算法能对无标签的数据进行分类。可视化结果显示了从基本网络结构利主成份分析(PCA)降维后的结果,并选取了前三个主成分的进行展示。
此外,学习算法能够沿着不同的主成分方向分离出各类数据。
结论
本文提出了一种基于元学习的无监督学习更新规则,实验结果表明算法的性能优于与现有的无监督学习算法。此外,更新规则可以训练不同宽度、深度和激活函数的模型。
大数据文摘后台对话框内回复“元学习”即可下载论文~
论文地址:
https://arxiv.org/pdf/1804.00222.pdf
【今日机器学习概念】
志愿者介绍
回复“志愿者”加入我们