OpenAI发布大规模元学习算法Reptile

作者：OpenAI

译者 & 编辑：Debra

AI 前线导读： 3 月 7 日，OpenAI 发布一种简单的元学习算法，称为 Reptile。该算法通过对任务进行重复采样并执行随机梯度下降，将初始参数更新为在该任务上学习到的最终参数。OpenAI 官博表示这种方法与 MAML（一种广泛适用的元学习算法 ）一样好用，但执行起来更简单，计算效率更高。

更多干货内容请关注微信公众号“AI 前线”，（ID：ai-front）

论文链接：

https://d4mucfpksywv.cloudfront.net/research-covers/reptile/reptile_update.pdf

伯克利关于 MAML 的论文：

http://bair.berkeley.edu/blog/2017/07/18/learning-to-learn/

代码链接：https://github.com/openai/supervised-reptile

元学习（Meta-learning） 是一种学习如何学习的过程。元学习算法会学习任务分布，其中每个任务都是一个需要学习的问题，算法会生成一个从少数例子中快速学习并举一反三的 learner。小样本学习（Few-shot Learning）分类问题是元学习中一个得到深入研究的问题，其中每个任务是一个分类问题，learner 只要从每个类的 1-5 个输入输出示例中学习，就能够对新的输入进行分类。以下是一个交互式 one-shot 演示，用 Reptile 进行单次分类。

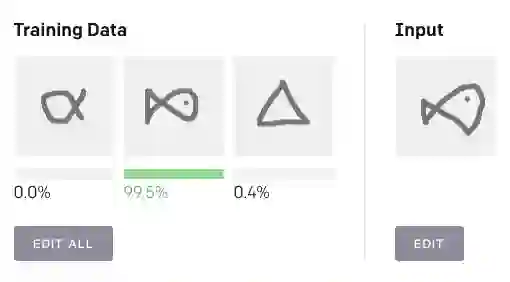
你可以单击“Edit All”按钮，绘制三个不同的形状或符号，然后再在右侧的输入字段中绘制其中一个，并查看 Reptile 如何对它们进行分类。前三张是标注样本：每张图都定义了一个类。第三张输入代表未知样本，最后 Reptile 将输出这张图片属于每个类别的概率。

 

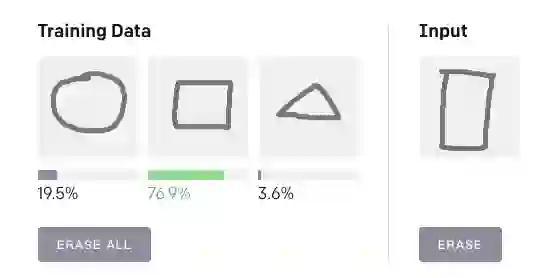
图 1

 

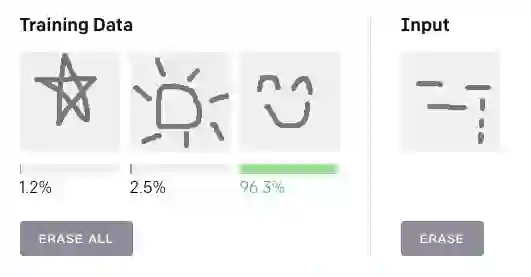
图 2

AI 前线用演示 demo 进行测试，结果显示，图 1 右侧输入结果中的长方形与左侧训练数据中的正方形明显属于同一类别；图 2 右侧哭脸与左侧训练图像中的笑脸同属于表情的类别，测试结果比较精准。

Reptile 工作原理

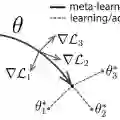
像 MAML 一样，Reptile 会学习神经网络的参数初始化方法，以便网络可以使用来自新任务的少量数据进行调适。但是，MAML 通过梯度下降算法的计算图展开微分计算过程，Reptile 只以标准方式对每个任务执行随机梯度下降（SGD），即它不展开计算图或计算任何二阶导数。这使得 Reptile 比 MAML 占用更少的计算和内存。伪代码如下：

Initialize Φ， the initial parameter vectorfor iteration 1,2,3,…doRandomly sample a task TPerform k>1 steps of SGD on task T, starting with parameters Φ resulting in parameters WUpdate: Φ←Φ+ϵ(W−Φ)end forReturn Φ

作为最后一步的替代方案，我们可以将Φ- w 作为梯度，并将其插入像 Adam https://arxiv.org/abs/1412.6980 这样更复杂的优化器。

一开始，这种方法的效果出人意料地好。如果 k=1，该算法对应“联合训练”——在多任务上运行 SGD。尽管联合训练可以在某些情况下学习到有用的初始化，但在零样本学习（zero-shot，例如当输出标签随机置换）时则行不通，学习到的甚少。Reptile 要求 k>1，更新依赖于损失函数的高阶导数；正如我们在论文中所展示的，这与 k = 1（联合训练）时的表现非常不同。

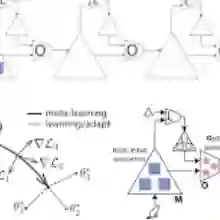
为了分析 Reptile 的工作原理，我们使用泰勒级数（Taylor series https://en.wikipedia.org/wiki/Taylor_series ）来进行近似更新。结果显示，Reptile 更新最大化同一任务中的不同小批量梯度内积，泛化得以改进。这一发现的影响可能超出元学习的范畴，解释了 SGD 的泛化特性。我们的分析表明，Reptile 和 MAML 执行了非常相似的更新，包括具备不同权重的相同两个项。

在实验中，我们证明了 Reptile 和 MAML 在 Omniglot 和 Mini-ImageNet 进行少量样本分类基准测试中的性能表现非常接近。而且由于更新具有较低的方差，Reptile 甚至收敛地更快。

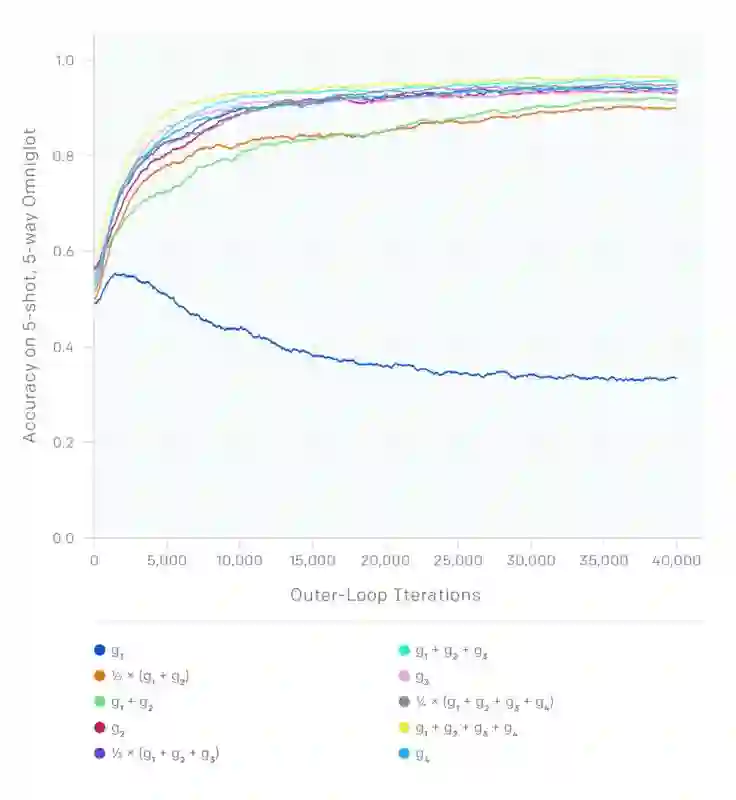
我们对 Reptile 的分析表明，我们可以使用不同的 SGD 梯度组合获得大量不同的算法。在下图中，假设我们在不同任务中使用不同批量大小的 SGD 执行 k 个步骤，会产生g1,g2,...,gk个梯度。下图显示了通过将每个和作为元梯度获得的 Omniglot 学习曲线。g2 对应一阶 MAML，这是一种在 MAML 原论文中提出的算法。由于方差减小，梯度增大，从而使得学习速度和收敛加快。请注意，仅使用 g1（对应 k=1）并取得产生本任务所预测那样的进展，因为零样本学习无法改善这一进程。

实现

GitHub 上有实现 Reptile 的详细说明 https://github.com/openai/supervised-reptile。

Reptile 使用 TensorFlow 进行相关计算，并包含用于在 Omniglot 和 Mini-ImageNet 上进行测试的代码。我们还发布了一个较小的基于 JavaScript 的实现 https://github.com/openai/supervised-reptile/tree/master/web，用于已经用 TensorFlow 预先训练的模型。

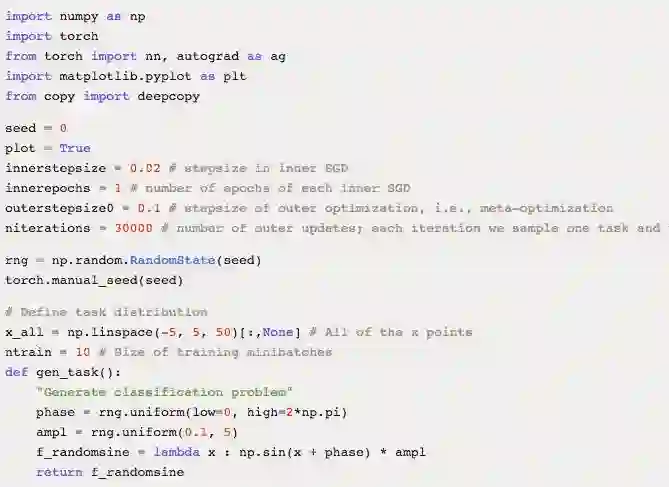
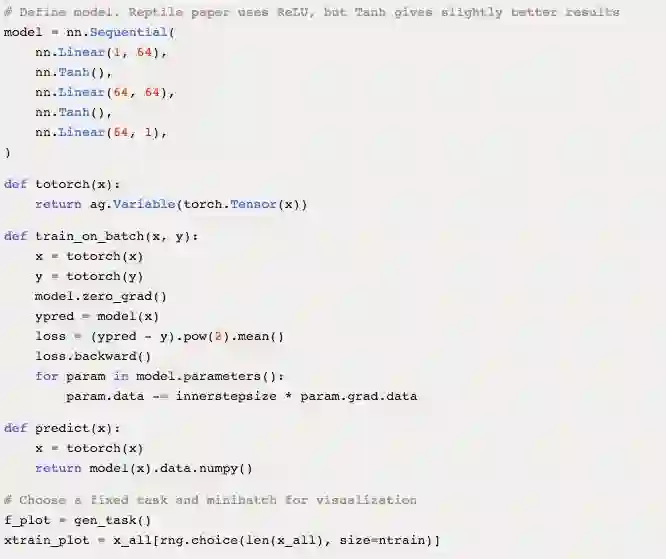
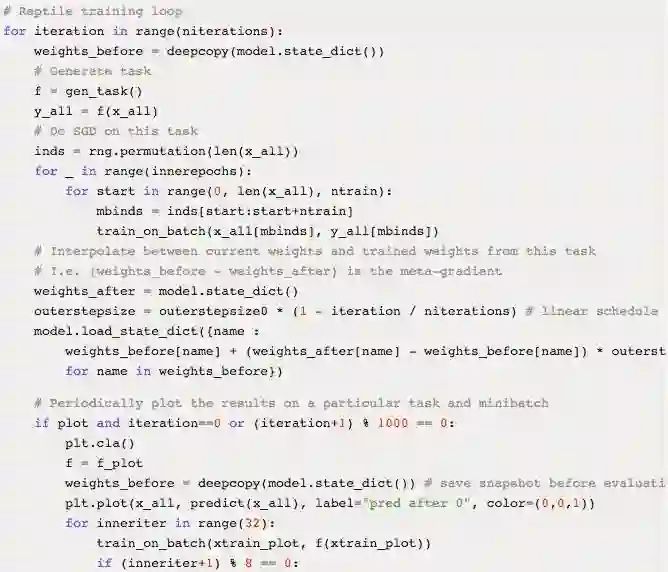
最后，下面是一个 few-shot 回归的简单示例，预测 10(x,y) 对的随机正弦波。该示例基于 PyTorch：

原文链接：https://blog.openai.com/reptile/

---

如果您觉得内容优质，记得给我们「留言」和「点赞」，给编辑鼓励一下！