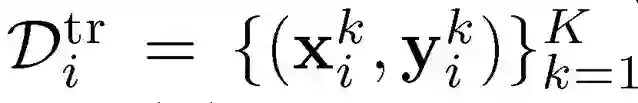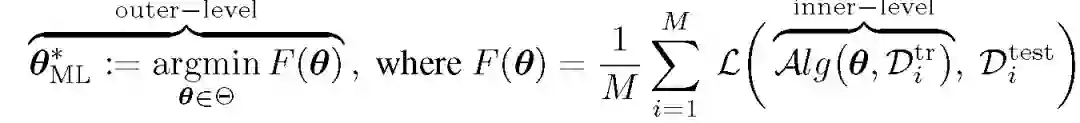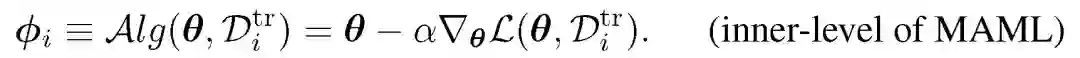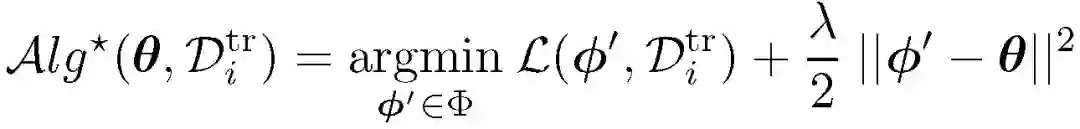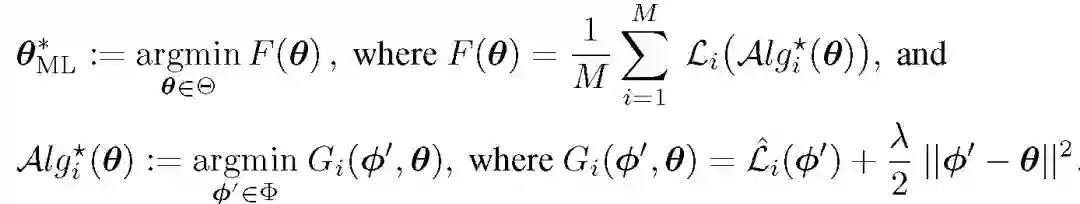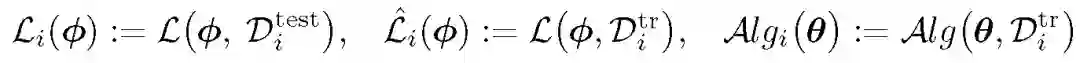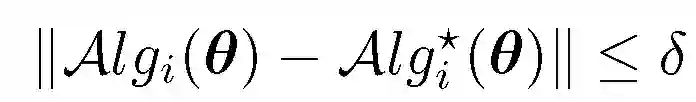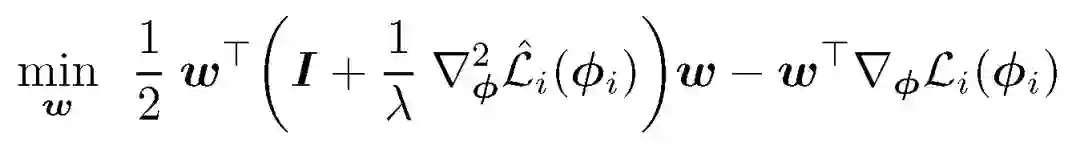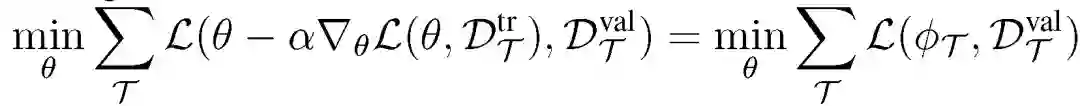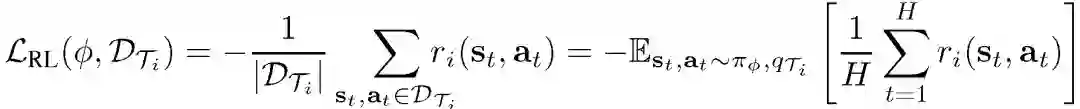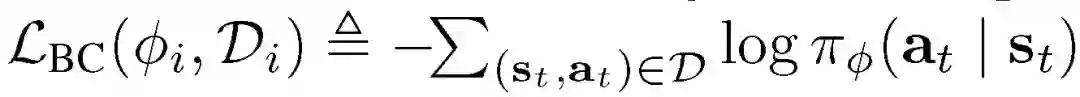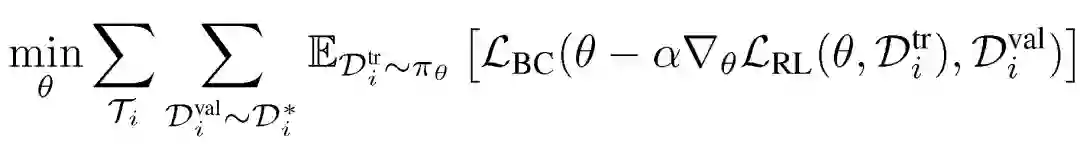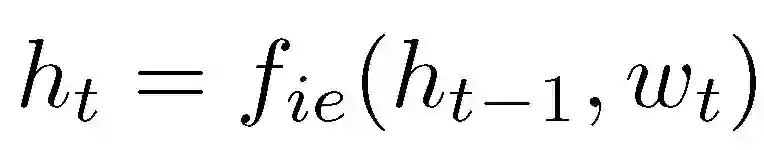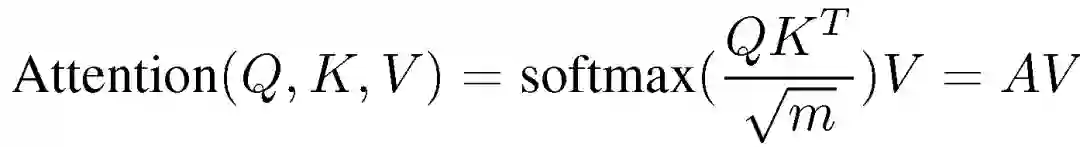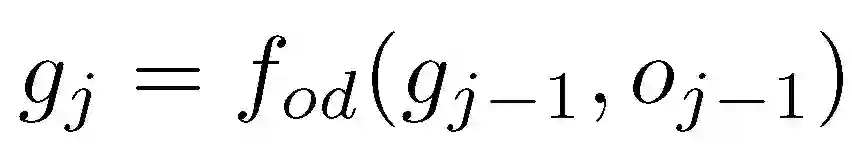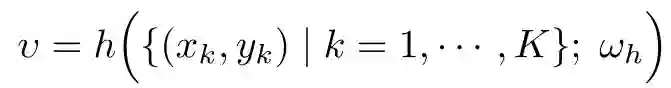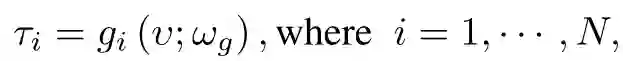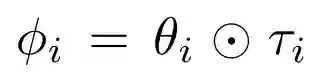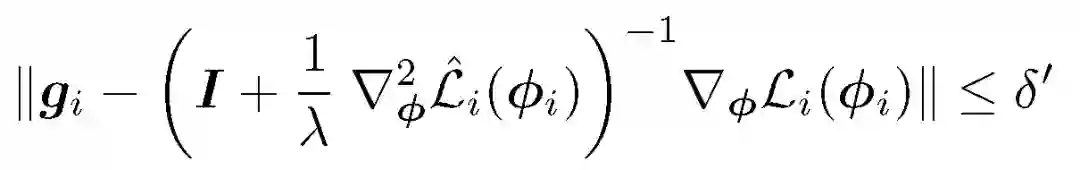NeurIPS提前看 | 四篇论文，一窥元学习的最新研究进展

2019 年 12 月 9 日 机器之心

机器之心原创

作者：仵冀颖

编辑：H4O

2019 年，NeurIPS 接受与元学习相关的研究论文约有 20 余篇。元学习（Meta-Learning）是近几年的研究热点，其目的是基于少量无标签数据实现快速有效的学习。本文对本次接收的元学习论文进行了梳理和解读。

2 019 年 NeurIPS 将于 12 月 8 日至 14 日在加拿大温哥华举行。 NeurIPS 今年共收到投稿 6743 篇，其中接受论文 1429 篇，接受率达到了 21.1%。作为人工智能领域的年度盛会，每年人工智能的专家学者以及工业企业界的研发人员都会积极参会，发布最新的理论研究结果以及应用实践方面的成果。今年，国外的高校和研究机构一如既往的踊跃参加本届 NeurIPS，其中 Google 共贡献了 179 篇文章，斯坦福和卡耐基梅隆分别有 79 篇和 75 篇文章。国内的企业界腾讯上榜 18 篇、阿里巴巴上榜 10 篇，高校和研究机构中清华参与完成的文章共有 35 篇。

2019 年，NeurIPS 接受与元学习相关的研究论文约有 20 余篇。元学习（Meta-Learning）是近几年的研究热点，其目的是基于少量无标签数据实现快速有效的学习。元学习通过首先学习与相似任务匹配的内部表示，为机器提供了一种使用少量样本快速适应新任务的方法。学习这种表示的方法主要有基于模型的（model-based meta-learning）和模型不可知的（model-agnostic meta-learning，MAML）两类。基于模型的元学习方法利用少量样本的任务标记（task identity）来调整模型参数，使用模型完成新任务，这种方法最大的问题是设计适用于未知任务的元学习策略非常困难。模型不可知的方法首先由 Chelsea Finn 研究组提出，通过初始化模型参数，执行少量的梯度更新步骤就能够成功完成新的任务。

本文从 NeurIPS 2019 的文章中选择了四篇来看看元学习的最新的研究方向和取得的成果。Chelsea Finn 以及他的老师 Pieter Abbeel 在元学习领域一直非常活跃，他们的研究团队在这个方向已经贡献了大量的优秀成果，推动了元学习在不同任务中的有效应用。在本次 NeurIPS 中，他们的研究团队针对基于梯度（或优化）的元学习提出了一种只依赖于内部级别优化的解决方案，从而有效地将元梯度计算与内部循环优化器的选择分离开来。另外，针对强化学习问题，提出了一种元强化学习算法，通过有监督的仿真学习有效的强化学习过程，大大加快了强化学习程序和先验知识的获取。我们将在这篇提前看中深入分析和理解这些工作。

Chelsea Finn 是斯坦福大学计算机科学和电子工程的助理教授，同时也担任 Google Brain 的研究科学家。Chelsea Finn 在她的博士论文《Learning to Learn with Gradients》中提出的 MAML 是目前元学习的三大方法之一，Chelsea Finn 证明了 MAML 的理论基础，并在元学习领域中将其发扬光大，在少样本模仿学习、元强化学习、少样本目标推断等中都获得了很好的应用。

本文还选择另外两篇关于元学习的文章进行讨论，其中一篇是 Facebook 的工作，提出了一种元序列到序列（Meta seq2seq）的方法，通过学习成分概括，利用域的代数结构来帮助理解新的语句。另外一篇提出了一个多模态 MAML（Multimodal MAML）框架，该框架能够根据所识别的模式调整其元学习先验参数，从而实现更高效的快速自适应。

论文清单：

Meta-Learning with Implicit Gradients
Guided Meta-Policy Search
Compositional generalization through meta sequence-to-sequence learning
Multimodal Model-Agnostic Meta-Learning via Task-Aware Modulation

1、Aravind Rajeswaran，Chelsea Finn，Sham Kakade，Sergey Levine，Meta-Learning with Implicit Gradients ，https://papers.nips.cc/paper/8306-meta-learning-with-implicit-gradients.pdf

基于优化的元学习方法主要有两种途径，一是直接训练元学习目标模型，即将元学习过程表示为神经网络参数学习任务。另一种是将元学习看做一个双层优化的过程，其中「内部」优化实现对给定任务的适应，「外部」优化的目标函数是元学习目标模型。本文是对后一种方法的研究和改进。元学习过程需要计算高阶导数，因此给计算和记忆带来不小的负担，另外，元学习还面临优化过程中的梯度消失问题。这些问题使得基于（双层）优化的元学习方法很难扩展到涉及大中型数据集的任务，或者是需要执行许多内环优化步骤的任务中。

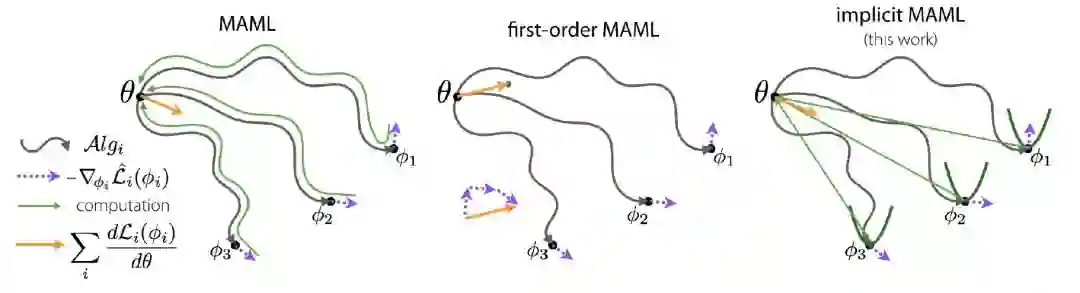
本文提出了一种隐式梯度元学习方法（implicit model-agnostic meta-learning，iMAML），利用隐式微分，推导出元梯度解析表达式，该表达式仅依赖于内部优化的解，而不是内部优化算法的优化路径，这就将元梯度计算和内部优化两个任务解耦。具体见图 1 中所示，其中经典的任务不可知的元学习（model-agnostic meta-learning,MAML）方法沿绿色的路径计算元梯度，一阶 MAML 则利用一阶倒数计算元梯度，本文提出的 iMAML 方法通过估计局部曲率，在不区分优化路径的情况下，推导出精确的元梯度的解析表达式。

图 1. 不同方法元梯度计算图示

针对元学习任务 {Ti},i=1,...,M，分别对应数据集 Di，其中每个数据集包含两个集（set）：训练集 D^tr 和测试集 D^test，每个集中的数据结构均为数据对，以训练集为例：

元学习任务 Ti 的目标是，通过优化损失函数 L，基于训练集学习任务相关的参数φ _i，从而实现测试集中的损失值最小。双层优化的元学习任务为：

其中，本文重点关注 Alg 部分的显示或隐式计算。经典 MAML 中，Alg 对应一步或几步梯度下降处理：

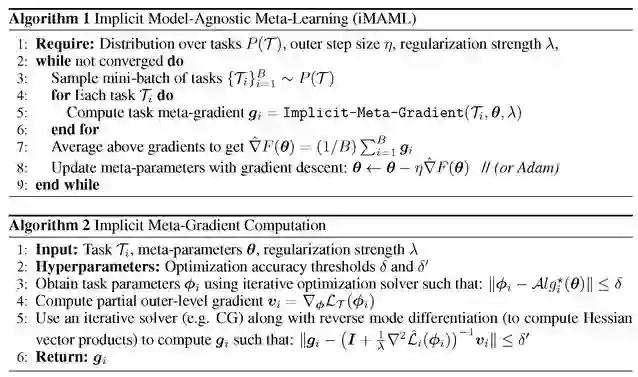
在数值计算过程中，为避免过拟合问题、梯度消失问题以及优化路径参数带来的计算和内存压力问题，采用显示正则化优化方法：

由此双层元学习优化任务为：

其中

采用显示迭代优化算法计算 Alg*存在下列问题：1、依赖于显示优化路径，参数计算和存储存在很大负担；2、三阶优化计算比较困难；3、该方法无法处理非可微分的操作。因此，本文考虑隐式计算 Alg*。具体算法如下：

考虑内部优化问题的近似解，它可以用迭代优化算法（如梯度下降）来获得，即：

对 Alg*的优化可以通过雅克比向量积近似逼近：

其中，φ_ i = Alg_i( θ)。观察到 g_i 可以作为优化问题的近似解获得：

共轭梯度算法（Conjugate Gradient, CG）由于其迭代复杂度和仅满足 Hessian 矢量积的要求而特别适合于求解此问题。不同方法的计算复杂度和内存消耗见表 1。用 k 来表示由 g_i 引起的内部问题的条件数，即内部优化计算问题的计算难度。Mem() 表示计算一个导数的内存负载。

表 1：不同方法的内存及计算负载

为了证明本文方法的有效性，作者给出了三个实验：

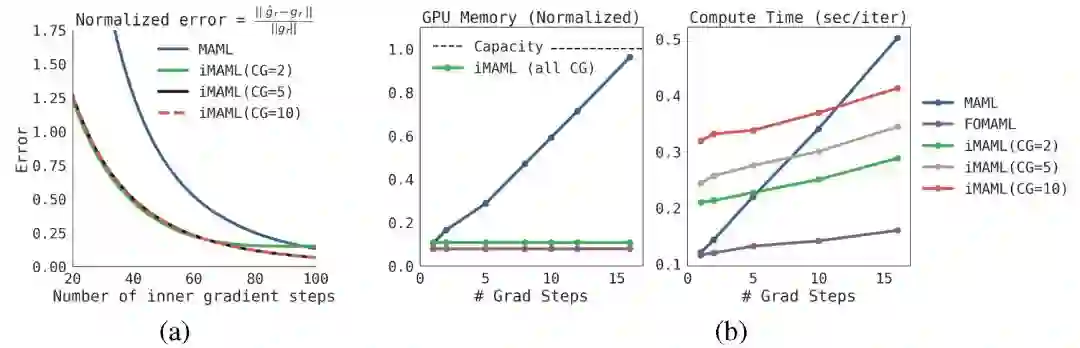
一是，通过实验验证 iMAML 是否能够准确计算元梯度。图 2（a）考虑了一个人工模拟的回归示例，其中的预测参数是线性的。iMAML 和 MAML 都能够渐近匹配精确的元梯度，但 iMAML 在有限迭代中能够计算出更好的近似。

图 2. 准确度、计算复杂度和内存负载对比。其中 MAML 为经典方法，iMAML 为本文提出的方法，FOMAML 为一阶 MAML 方法

二是，通过实验验证在有限迭代下 iMAML 是否能够比 MAML 更精确地逼近元梯度。图 2(b) 中实验可知，iMAML 的内存是基于 Hessian 向量积的，与内部循环中梯度下降步数无关。内存使用也与 CG 迭代次数无关，因为中间计算不需要存储在内存中。MAML 和 FOMAML 不通过优化过程反向传播，因此计算成本仅为执行梯度下降的损耗。值得注意的是，FOMAML 尽管具有较小的计算复杂度和内存负载，但是由于它忽略了 Jacobian，因此 FOMAML 不能够计算精确的元梯度。

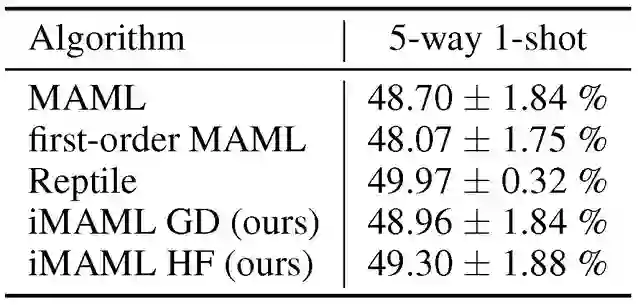
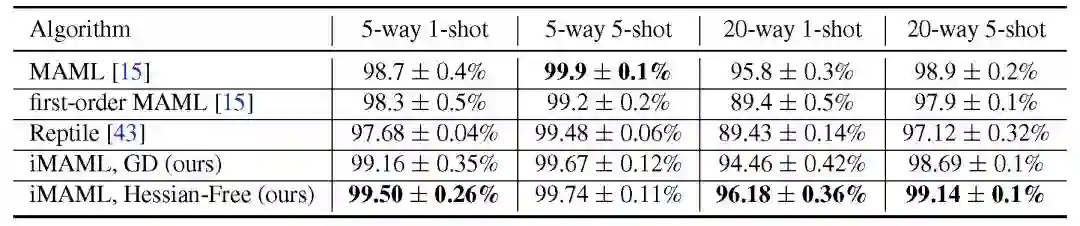
三是，对比与 MAML 相比的计算复杂度和内存负载，以及通过实验验证 iMAML 是否能在现实的元学习问题中产生更好的结果，本文使用了 Omniglot 和 Mini ImageNet 的常见少数镜头图像识别任务（few-shot）进行验证。在现实元学习实验中，选择了 MAML、FOMAML (First order MAML) 和 Reptile 作为对比方法。在 Omniglot 域上，作者发现 iMAML 的梯度下降（GD）版本与全 MAML 算法相比具有竞争力，并且在亚空间上优于其近似值（即 FOMAML 和 Reptile），特别是对于较难的 20 路（20-way）任务。此外，实验还表明无 Hessian 优化的 iMAML 比其他方法有更好的性能，这表明内部循环中强大的优化器可以改进元学习的效果。在 Mini-ImageNet 域中，iMAML 的效果也优于 MAML 和 FOMAML。

表 2. Omniglot 实验结果

表 3. Mini ImageNet 实验结果

2、Russell Mendonca，Abhishek Gupta，Rosen Kralev，Pieter Abbeel，Sergey Levine，Chelsea Finn，Guided Meta-Policy Search，https://papers.nips.cc/paper/9160-guided-meta-policy-search.pdf

元学习的目的是利用完成不同任务的历史经验帮助学习完成新任务的技能，元强化学习通过与环境的少量交互通过尝试和改正错误来解决这一问题。元强化学习的关键是使得 agent 具有适应性，能够以新的方式操作新对象，而不必为每个新对象和目标从头学习。目前元强化学习在优化稳定性、解决样本复杂度等方面还存在困难，因此主要在简单的任务领域中应用，例如低维连续控制任务、离散动作指令导航等。

本文的研究思路是：元强化学习是为了获得快速有效的强化学习过程，这些过程本身不需要通过强化学习直接获得，相反，可以使用一个更加稳定和高效的算法来提供元级（meta-level）监控，例如引入监督模仿学习。本文首次提出了在元学习环境中将模仿（imitation）和强化学习（RL）相结合。在执行元学习的过程中，首先由本地学习者单独解决任务，然后将它们合并为一个中心元学习者。但是，与目标是学习能够解决所有任务的单一策略的引导式策略搜索（guided policy search）不同，本文提出的方法旨在元学习到能够适应训练任务分布的单一学习者，通过概括和归纳以适应训练期间未知的新任务。

图 3. 引导式元策略搜索算法综述

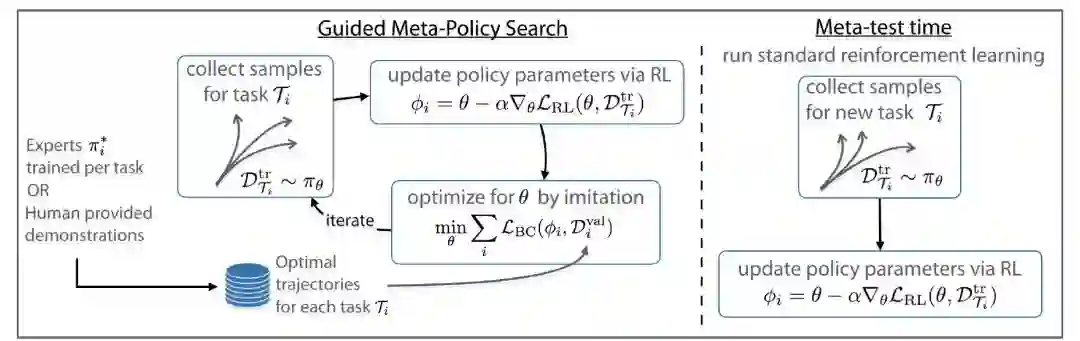
图 3 给出本文提出的引导式元策略搜索算法的总体结构。通过在内部循环优化过程中使用增强学习以及在元优化过程引入监督学习，学习能够快速适应新任务的策略π_θ。该方法将元学习问题明确分解为两个阶段：任务学习阶段和元学习阶段。此分解使得可以有效利用以前学习的策略或人工提供的演示辅助元学习。

现有的元强化学习算法一般使用同步策略方法（on-policy）从头开始进行元学习。在元训练期间，这通常需要大量样本。本文的目标是使用以前学到的技能来指导元学习过程。虽然仍然需要用于内部循环采样的同步策略数据，但所需要的数据比不使用先前经验的情况下要少得多。经典 MAML 的目标函数如下：

应用于元强化学习中，每个数据集表示为如下轨迹形式：s_1,a_1,...,a_H-1,,s_H。内部和外部循环的损失函数为：

将元训练任务的最优或接近最优的策略标记为 {(π_i)^*}，其中每个政策定义为「专家」。元学习阶段的优化目标 L_RL(φ_i,D_i) 与 MAML 相同，其中φ_i 表示策略参数，D_i 为数据集。

内部策略优化过程利用第一阶段学习到的策略优化元目标函数，特别的，把外部目标建立在专家行为的监督模仿或行为克隆（Behavior Cloning，BC）上。BC 损失函数为：

监督学习的梯度方差较小，因此比强化学习的梯度更加稳定。第二阶段的任务是：首先利用每个策略 (π_i)^*，为每个元训练任务 Ti 收集专家轨迹 (Di)^*的数据集。使用此初始数据集，根据以下元目标更新策略：

由此得到一些能够适用于不同任务的列初始策略参数θ从而生成φ_i。在单任务模拟学习环境中，进一步的，可以继续通过从学习到的策略中收集额外的数据 (扩展数据集 D*)，然后用专家策略中的最优操作标记访问状态。具体步骤为：（1）利用策略参数θ生成 {φ_i}；（2）针对每个任务，利用当前策略 {π_(φ_i)} 生成状态 {{s_t}_i}；（3）利用专家生成监督数据 D={{s_t,π_i(s_t))}_i}；（4）使用现有监督数据聚合该数据。

引导式元策略搜索算法（Guided Meta-policy Search, GMPS）如下：

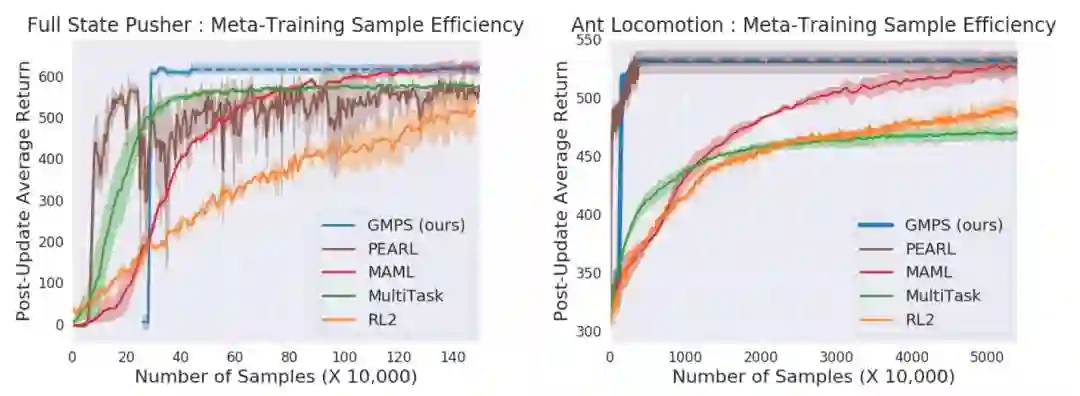
本文使用 Sawyer 机器人控制任务和四足步行机任务验证 GMPS 的有效性。所选择的对比算法包括：基于异步策略方法的 PEARL、策略梯度版本的 MAML（内部循环使用 REINFORCE，外部循环使用 TRPO）、RL2、针对所有元训练任务的单一政策方法 MultiTask、附加结构化噪声的模型不可知算法 (MAESN)。图 4 给出完成全状态推送任务和密集奖励运动的元训练效率。所有方法都达到了相似的渐近性能，但 GMPS 需要的样本数量明显较少。与 PEARL 相比，GMPS 给出了相近的渐进性能性能。与 MAML 相比，GMPS 完成 Sawyer 物体推送任务的性能提高了 4 倍，完成四足步行机任务的性能提高了约 12 倍。GMPS 的下述处理方式：（1）采用了用于获取每个任务专家的异步策略增强学习算法和（2）能够执行多个异步策略监督梯度步骤的组合，例如外部循环中的专家，使得 GMPs 与基于策略的元增强学习算法（如 MAML）相比，获得了显著的总体样本效率增益，同时也显示出比 PEARL 等数据效率高的上下文方法更好的适应性。

图 4. Sawyer 机器人任务效果对比

图 5. 稀疏奖励开门动作（左）、稀疏奖励蚂蚁移动（中）和视觉推手动作（右）的元训练比较

对于涉及稀疏奖励和图像观察的具有挑战性的任务，有效利用人工提供的演示可以极大地改进强化学习的效果，图 5 中给出了相关的实验。与其他传统方法相比，GMPS 能够更加有效且容易的利用演示信息。在图 5 所有的实验中，关于目标位置的位置信息都不作为输入，而元学习算法必须能够发现一种从奖励中推断目标的策略。对于基于视觉的任务，GMPS 能够有效地利用演示快速、稳定地学习适应。此外，图 5 也表明，GMPS 能够在稀疏的奖励设置中成功地找到一个好的解决方案，并学会探索。GMPS 和 MAML 都能在所有训练任务中获得比单一策略训练的强化学习更好的性能。

3、Brenden M. Lake，Compositional generalization through meta sequence-to-sequence learning，https://papers.nips.cc/paper/9172-compositional-generalization-through-meta-sequence-to-sequence-learning.pdf

由于人具有创作学习的能力，他们可以学习新单词并立即能够以多种方式使用它们。一旦一个人学会了动词「to Facebook」的意思，他或她就能理解如何「慢慢地 Facebook」、「急切地 Facebook」或「边走边 Facebook」。这就是创造性的能力，或是通过结合熟悉的原语来理解和产生新颖话语的代数能力。作为一种机器学习方法，神经网络长期以来一直因缺乏创造性而受到批评，导致批评者认为神经网络不适合建模语言和思维。最近的研究通过对现代神经结构的研究，重新审视了这些经典的评论，特别是成功的将序列到序列（seq2seq）模型应用于机器翻译和其他自然语言处理任务中。这些研究也表明，在创造性的概括方面，seq2seq 仍存在很大困难，尤其是需要把一个新的概念（「到 Facebook」）和以前的概念（「慢慢地」或「急切地」）结合起来时。也就是说，当训练集与测试集相同时，seq2seq 等递归神经网络能够获得较好的效果，但是当训练集与测试集不同，即需要发挥「创造性」时，seq2seq 无法成功完成任务。

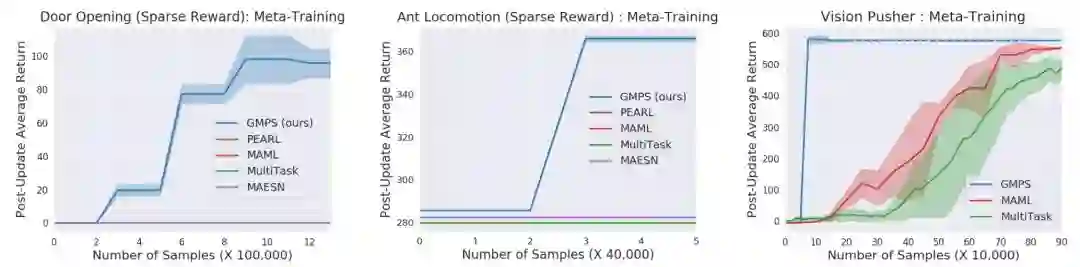
这篇文章中展示了如何训练记忆增强神经网络，从而通过「元-序列到序列学习」方法（meta seq2seq）实现创造性的概括。与标准的元学习方法类似，在「元训练」的过程中，训练是基于分布在一系列称为「集（episode）」的小数据集上完成的，而不是基于单个静态数据集。在「元 seq2seq 学习」过程中，每一集（episode）都是一个新的 seq2seq 问题，它为序列对（输入和输出）和「查询」序列（仅输入）提供「支持」。该方法的网络支持将序列对加载到外部内存中，以提供为每个查询序列生成正确输出序列所需的上下文。将网络的输出序列与目标任务进行比较，从而获得由支持项目到查询项目的创造性概括能力。元 seq2seq 网络对需要进行创造性组合泛化的多个 seq2seq 问题进行元训练，目的是获得解决新问题所需的组合技能。新的 seq2seq 问题完全使用网络的激活动力学和外部存储器来解决；元训练阶段结束后，不会进行权重更新。通过其独特的结构选择和训练过程，网络可以隐式地学习操作变量的规则。

图 6. 元 seq2seq 学习

图 6 给出了一个元 seq2seq 学习的示例，其任务是根据支撑数据集处理查询指令「跳两次」，支撑集包括「跑两次」、「走两次」、「看两次」和「跳」。利用一个递归神经网络（Recurrent Neural Network，RNN）编码器（图 6 中右侧下部的红色 RNN）和一个 RNN 解码器（图 6 中右侧上部绿色 RNN）理解输入语句生成输出语句。这个结构与标准 seq2seq 不同，它利用了支撑数据集、外部存储和训练过程。当消息从查询编码器传递到查询解码器时，它们受到了由外部存储提供的逐步上下文信息 C 影响。

下面将详细描述体系结构的内部工作流程：

1、输入编码器

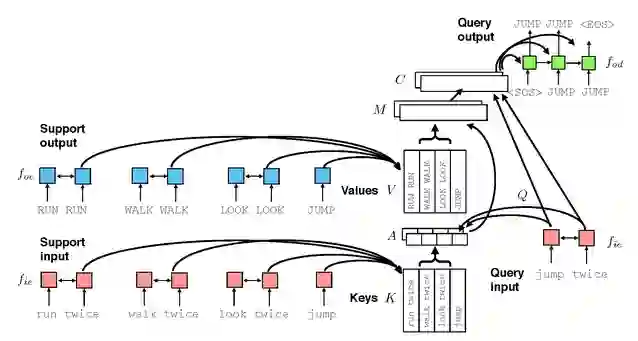
输入编码器 f_ie（图 6 中红色部分）对输入查询指令以及支撑数据集中的输入指令进行编码，生成输入嵌入特征 w_t，利用 RNN 转化为隐层嵌入特征 h_t：

对于查询序列，在每个步骤 t 时的嵌入特征 h_t 通过外部存储器，传递到解码器。对于每个支撑序列，只需要最后一步隐藏嵌入特征，表示为 K_i。这些向量 K_i 作为外部键值存储器中的键使用。本文使用的是双向长短时记忆编码（bidirectional long short-term memory encorders）方法。

2、输出编码器

输出编码器 f_oe（图 6 中蓝色部分）用于每个支撑数据集中的项目和其对应的输出序列。首先，编码器使用嵌入层嵌入输出符号序列（例如动作）。第二，使用与 f_ie 相同的处理过程计算数列的嵌入特征。最后一层 RNN 的状态作为支撑项目的特征向量存储 V_i。仍然使用 biLSTM。

3、外部存储器

该架构使用类似于存储器网络的软键值存储器，键值存储器使用的注意函数为：

每个查询指令从 RNN 编码器生成 T 个嵌入，每个查询符号对应一个，填充查询矩阵 Q 的行。编码的支撑项目分别为输入和输出序列的 K 行和 V 行。注意权重 A 表示对于每个查询步骤，哪些内存单元处于活动状态。存储器的输出是矩阵 M=AV，其中每一行是值向量的加权组合，表明查询输入步骤中每一步的存储器输出。最后，通过将查询输入嵌入项 h_t 和分步内存输出项 M_t 与连接层 C_t=tanh（Wc1 [h_t；M_t]）结合来计算分步上下文，从而生成分步上下文矩阵 C。

4、输出解码器

输出解码器将逐步上下文 C 转换为输出序列（图 6 中绿色部分）。解码器将先前的输出符号嵌入为向量 o_j-1，该向量 o_j-1 与先前的隐藏状态 g_j-1 一起啊输入到 RNN（LSTM）以获得下一个隐藏状态，

初始隐藏状态 g_0 被设置为最后一步的上下文 C_T。使用 Luong 式注意计算解码器上下文 u_j，使得 u_j=Attension（g_j，C，C）。这个上下文通过另一个连接层 g_j=tanh（Wc2 [g_j；u_j]），然后映射到 softmax 输出层以产生输出符号。此过程重复，直到产生所有输出符号，RNN 通过产生序列结束符号来终止响应。

5、元训练

元训练通过一系列训练集优化网络，每个训练集都是一个带有 n_s 支撑项目和 n_q 查询项目的新 seq2seq 问题。模型的词汇表是事件（episode）词汇表的组合，损失函数是查询的预测输出序列的负对数似然。

本文方法的 PyTorch 代码已公开发布：https://github.com/brendenlake/meta_seq2seq

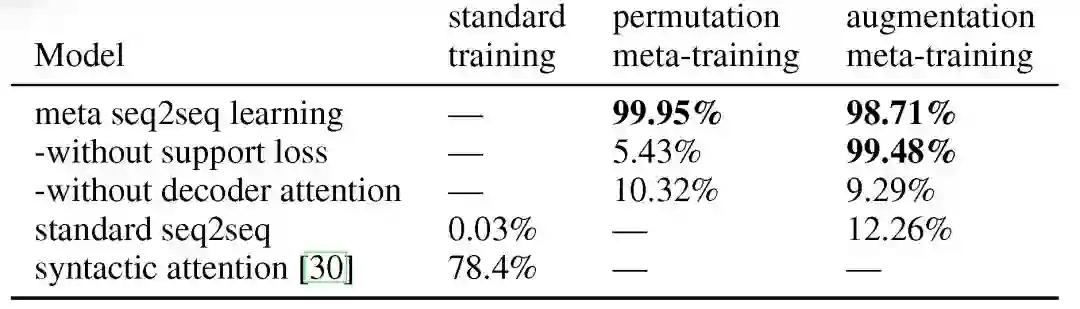
本文给出了不同的实验验证元 seq2seq 方法的有效性。通过置换元训练增加一个新的原语的实验，评估了元 seq2seq 学习方法在添加新原语的 SCAN 任务中的效果。通过将原始 SCAN 任务分解为一系列相关的 seq2seq 子任务，训练模型进行创造性的概括。目标是学习一个新的基本指令，并将其组合使用。例如模型学习一个新的原始「跳跃」，并将其与其他指令结合使用，类似于本文前面介绍的「to Facebook」示例。实验结果见表 4 结果中间列。其中，标准 seq2seq 方法完全失败，正确率仅为 0.03%。元 seq2seq 方法能够成功完成学习复合技能的任务，表中所示达到了平均 99.95% 的正确率。

表 4. 在不同训练模式下测试 SCAN「添加跳跃」任务的准确性

通过增强元训练增加一个新的原语的实验目的是表明元 seq2seq 方法可以「学习如何学习」原语的含义并将其组合使用。文章只考虑了四个输入原语和四个意义的非常简单的实验，目前的研究情况下，作者认为尚不能确定元 seq2seq 学习是否适用于更复杂的任务领域。实验结果见表 4 的最右侧列。元 seq2seq 方法能够完成获得指令「跳」并正确使用的任务，正确率达到了 98.71%。标准 seq2seq 得益于增强训练的处理得到了 12.26% 的正确率。

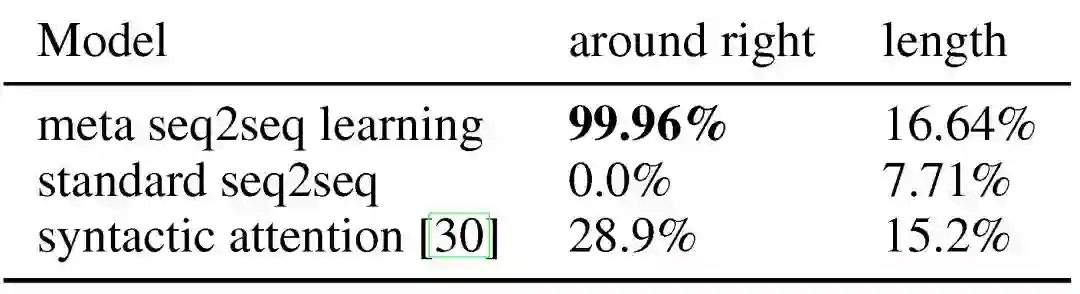
关于利用元训练合成类似概念的任务，实验结果见表 5 左侧结果列。元 seq2seq 学习方法能够近乎完美的完成这个任务（正确率 99.96%），能够根据其组成部分推断「around right」的含义。而标准 seq2seq 则完全无法完成这个任务（0.0% 正确率），syntactic attention 方法完成这个任务的正确率为 28.9%。最后一个实验验证了元 seq2seq 方法是否能够学习推广到更长的序列，即测试序列比元训练期间的任何经验语句序列都长。实验结果见表 5 最右侧列。可以看到，所有方法在这种情况下表现都不佳，元 seq2seq 方法仅有 16.64% 的正确率。尽管元 seq2seq 方法在合成任务上较为成功，但它缺乏对较长序列进行外推所需的真正系统化的概括能力。

表 5. 测试 SCAN「左右」和「长度」任务的准确性

元 seq2seq 学习对于理解人们如何从基本成分元素创造性的概括推广到其它概念有着重要的意义。

人们是在动态环境中学习的，目的是解决一系列不断变化的学习问题。在经历过一次像「to Facebook」这样的新动词之后，人们能够系统地概括这种学习或激励方式是如何完成的。这篇文章的作者认为，元学习是研究学习和其他难以捉摸的认知能力的一个强大的新工具，尽管，在目前的研究条件下还需要更多的工作来理解它对认知科学的影响。

本文所研究的模型只是利用了网络动态参数和外部存储器就实现了在测试阶段学到如何赋予单词新的意义。虽然功能强大，但这个工作仍然是一个有限的「变量」概念，因为它需要熟悉元训练期间所有可能的输入和输出分配。这是目前所有神经网络体系架构所共有的问题。作者在文末提到，在未来的工作中，打算探索在现有网络结构中添加更多的象征性组织（symbolic machinery），以处理真正的新符号，同时解决推广到更长输出序列的挑战。

4、Risto Vuorio，Shao-Hua Sun，Hexiang Hu，Joseph J. Lim，Multimodal Model-Agnostic Meta-Learning via Task-Aware Modulation，https://papers.nips.cc/paper/8296-multimodal-model-agnostic-meta-learning-via-task-aware-modulation.pdf

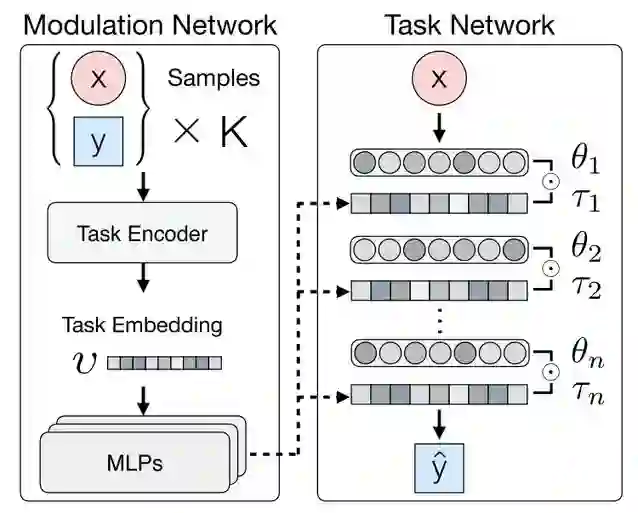
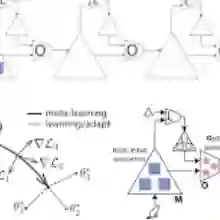
经典的模型不可知的元学习方法（MAML）需要找到在整个任务分布中共享的公共初始化参数。但是，当任务比较复杂时，针对任务采样需要能够找到实质性不同的参数。本文的研究目标是，基于 MAML，找到能够获得特定模式的先验参数的元学习者，快速适应从多模式任务分布中抽取的给定任务。本文提出了一个多模态模型不可知元学习框架（Multimodal Model-Agnostic Meta-Learning，MMAML），该框架同时利用基于模型的元学习方法和模型不可知的元学习方法，能够根据识别的模式调整其元学习先验参数，从而实现更高效的快速自适应。图 7 给出了 MMAML 整体框架。MMAML 的重点是利用两种神经网络实现快速适应新任务。首先，称为调制网络（Modulation Network）的网络预测任务模式的标识。然后将预测出的模式标识作为任务网络 (Task Network）的输入，该网络通过基于梯度的优化进一步适应任务。具体算法如下：

图 7. MMAML 框架

调制网络负责识别采样任务的模式，并生成一组特定于该任务的参数。首先将给定的 K 个数据及其标签 {x_k，y_k}_k=1，…，K 输入到任务编码器 f 中，并生成一个嵌入向量 v，该向量对任务的特征进行编码：

然后基于编码后的任务嵌入向量 v 计算任务特定参数 τ，进而对任务网络的元学习先验参数进行调制。任务网络可以是任意参数化的函数，例如深卷积网络、多层递归网络等。为了调整任务网络中每个块的参数作为解决目标任务的初始化参数，使用块级转换来缩放和移动网络中每个隐藏单元的输出激活。具体地，调制网络为每个块 i 产生调制向量，表示为：

其中 N 是任务网络中的块数。上述过程表示

其中θ_i 为初始化参数，Φ_i 是任务网络的调制先验参数。本文选用了特征线性调制方法（feature-wise linear modula-

tion，FiLM）作为调制运算方法。

使用调制网络生成的任务特定参数τ={τ_i | i=1，···，N} 来调制任务网络的每个块的参数，该参数可以在参数空间 f（x;θ,τ）中生成模式感知初始化。在调制步骤之后，对任务网络的元学习先验参数进行几步梯度下降以进一步优化任务τ_i 的目标函数。在元训练和元测试时，采用了相同的调制和梯度优化方法。

作者表示，详细的网络结构和训练超参数会因应用领域的不同而有所不同。本文在多模态任务分布下，评估了 MMAML 和基线极限方法在不同任务中的效果，包括回归、图像分类和强化学习等。基线对比方法包括使用多任务网络的 MAML 和 Multi-MAML。

表 6. 回归实验结果

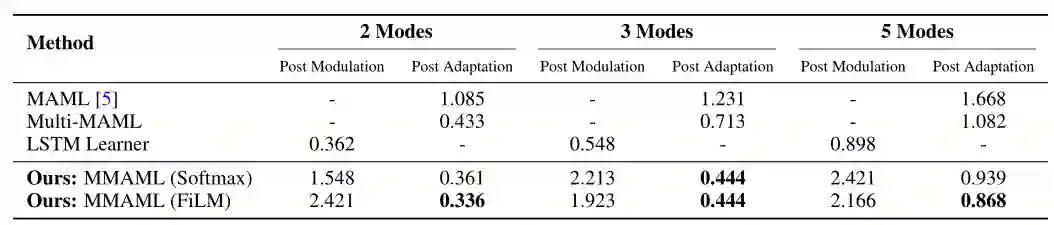
表 6 给出了 2、3 和 5 模式下多模态五次回归的均方误差（MSE）。应用μ=0 和σ=0.3 的高斯噪声。Multi-MAML 方法使用基本事实的任务模式来选择对应的 MAML 模型。本文提出的方法（使用 FiLM 调制）比其他方法效果稍好。

表 7. 图像分类实验结果

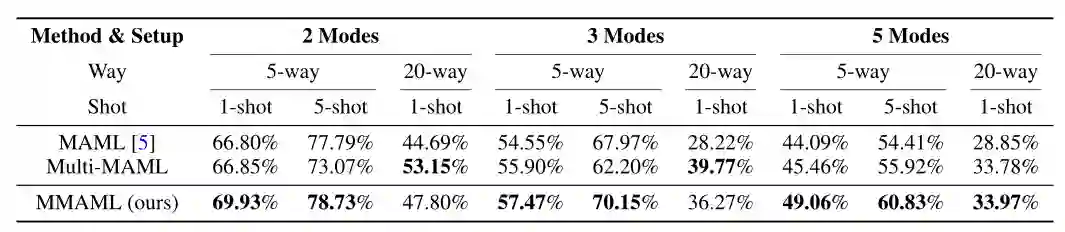
表 7 给出了 2、3、5 模式多模式少镜头图像分类准确度测试结果，结果证明了本文提出的方法与 MAML 比有较好的效果，并且与 Multi-MAML 的性能相当。

表 8. 元强化学习实验结果

表 8 给出在 3 个随机种子上报告的 2、4 和 6 个模式的多模态强化学习问题中，每集（episode）累积奖励的平均值和标准差。元强化学习的目标是在有限的任务经验基础上适应新的任务。本文使用 ProMP 算法优化策略和调制网络，同时使用 ProMP 算法作为实验对比基线，Multi-ProMP 是一个人工基线，用于显示使用 ProMP 为每个模式训练一个策略的性能。表 8 所示的实验结果表明，MMAML 始终优于未经调制的 ProMP。只考虑单一模式的 Multi-ProMP 所展示出的良好性能表明，在该实验环境下，不同方法面临的适应性困难主要来自于多种模式。

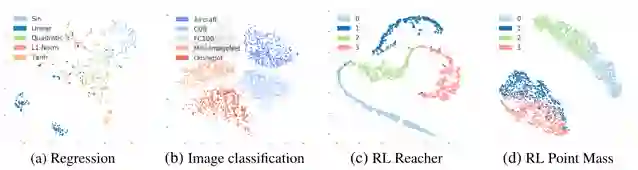
图 8. 从随机抽样的任务生成的任务嵌入的 tSNE 图；标记颜色表示任务分布的不同模 式

最后，图 8 给出了上述各个实验从随机抽样的任务生成的任务嵌入的 tSNE 图，其中标记颜色表示任务分布的不同模式。图（b）和图（d）显示了根据不同任务模式的清晰聚类，这表明 MMAML 能够从少量样本中识别任务并产生有意义的嵌入量。（a）回归：模式之间的距离与函数相似性的情况一致（例如，二次函数有时可以类似于正弦函数或线性函数，而正弦函数通常不同于线性函数）（b）少镜头图像分类：每个数据集（即模式）形成自己的簇。（c）-（d）强化学习：聚类数字代表不同的任务分配模式。不同模式的任务在嵌入空间中能够清晰地聚集在一起。

作者介绍：仵冀颖，工学博士，毕业于北京交通大学，曾分别于香港中文大学和香港科技大学担任助理研究员和研究助理，现从事电子政务领域信息化新技术研究工作。主要研究方向为模式识别、计算机视觉，爱好科研，希望能保持学习、不断进步。

机器之心「SOTA模型」：22大领域、127个任务，机器学习 SOTA 研究一网打尽。