天使长加百利的托里拆利小号 | 数学思考法:解析直觉与谎言
下文节选自《 数学思考法:解析直觉与谎言》,已获图灵授权,【遇见数学】特此表示感谢!
《数学思考法:解析直觉与谎言》
相关链接:
» 颠覆直觉的图形:井盖与50 便士
» 惊人的“同月同日生”
托里拆利小号
今天的这个问题,总让我觉得有点儿不对劲儿,这种题应该没人能解出来吧?因为根本就没有答案!
问题
12 月 7 日
存在一个杯子,杯子的容量是有限的,但即使用尽地球上所有玻璃材料,也不足以制作出这个杯子。这个杯子究竟应该如何制作呢?
“即使用尽地球上所有玻璃材料,也不足以制作出这个杯子”,意思是说这个杯子的表面积是无穷大的,也就是说这个杯子表面是无限延伸的。但是这样的话,它的体积也应该会同步增大的啊,题里面却又说到“容量是有限的”,这难道不是自相矛盾的命题吗?
有限的体积与无限的表面积
难怪 X 先生会不服气,这个问题乍看上去确实有点儿古怪,有悖于常人的直觉。另外,这个问题也有别于之前的问题,我们无法通过实际动手去一试究竟。只能通过思考,也就是所谓的思想实验来进行验证。
换句话说,这道题也可以理解为:“如何在理论上构造一个体积有限、表面积无限的图形。”
这么想来,命题就是要设计一个特殊的容器,为了使理论设想的过程更为形象,我们可以将其想象为一个现实中存在的容器,比如一个玻璃茶杯。
对于茶杯来说,使用者关注的是“这个茶杯究竟可以装多少水”;而茶杯的生产制造者则更加关注“制造茶杯究竟要耗费多少原材料”。这和我们理论设想中的要点是一致的。
为了方便推导,我们要进行一些理想化假设。首先假设玻璃茶杯的厚度无穷小,小到可以忽略不计。这样的话,在茶杯上盖上一个非常薄的茶盖,整个茶杯的体积就近似等于其容量(容积)。
茶杯的表面积,则基本决定了制造茶杯需要多少原料(玻璃)。基于上述假设,我们再回过头来思考本节开篇处 X 先生试图解答的问题:
问题
12 月 7 日
存在一个杯子,杯子的容量是有限的,但即使用尽地球上所有玻璃材料,也不足以制作出这个杯子。这个杯子究竟应该如何制作呢?
我们先从数学的角度来考虑,满足上述条件的杯子是什么形状。
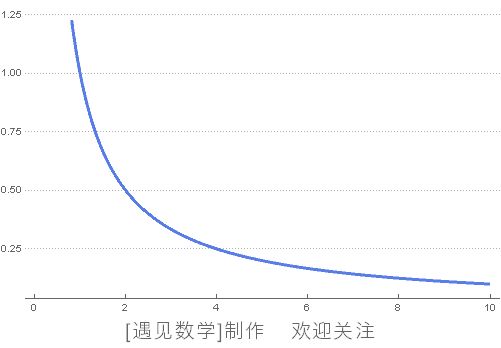
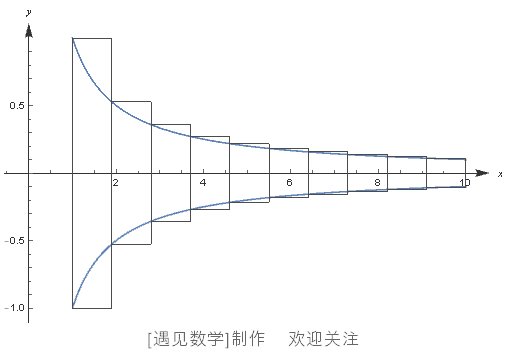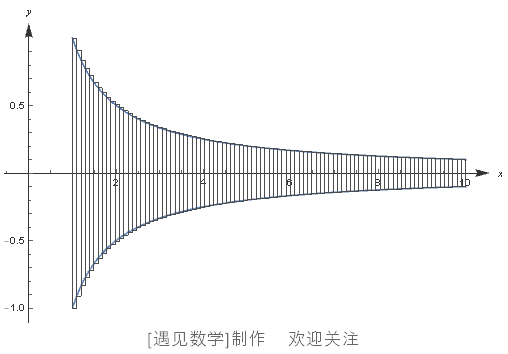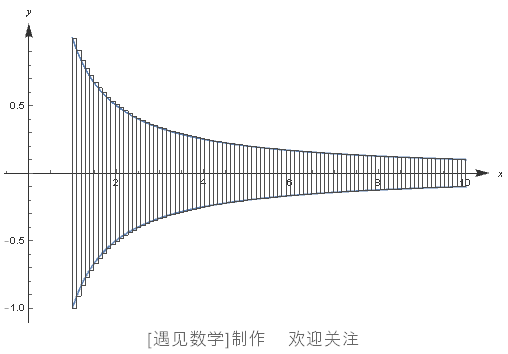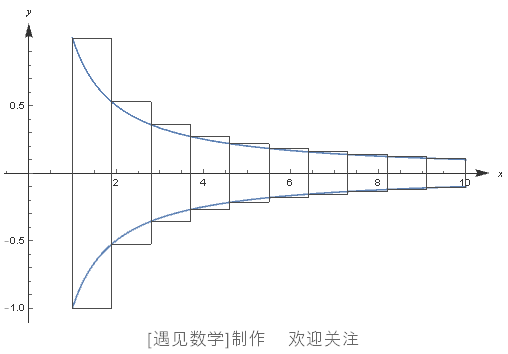
首先,给出一个无线延伸的反比例函数曲线 y = 1/x (图 102)。可以观察到当 x = 0 时,y 的值是趋近于无限大的,因此为便于论证,我们以 x = 1 为节点,对这条无线延伸的曲线进行截取。这样就可以得到一条极度细长的曲线,这条曲线是向坐标轴右侧无限延伸的。当然,图 102 中只给出了这条曲线有限的一段,理论上,完整地呈现出来的话应该是像一条无限延伸的细长尾巴。
图 102 反比例函数曲线
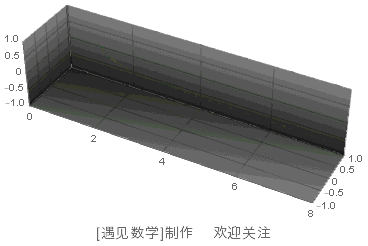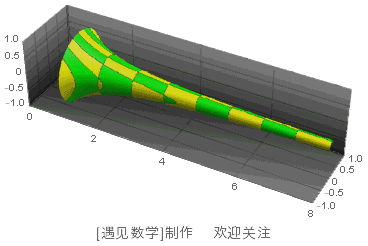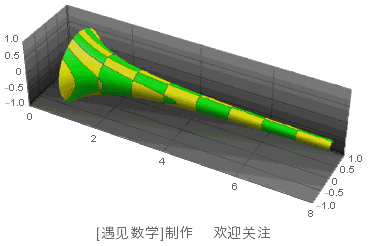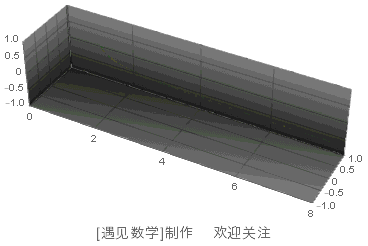
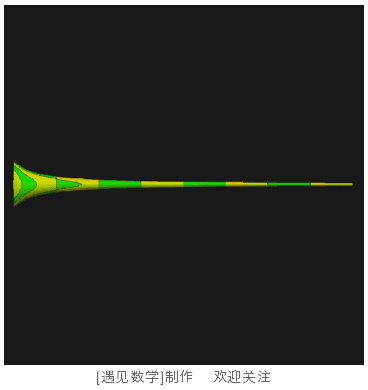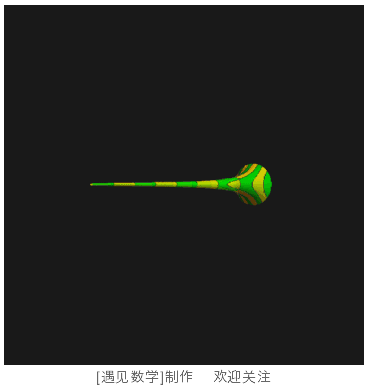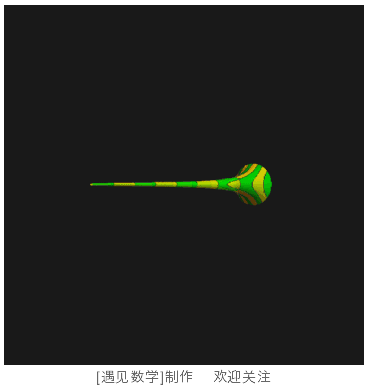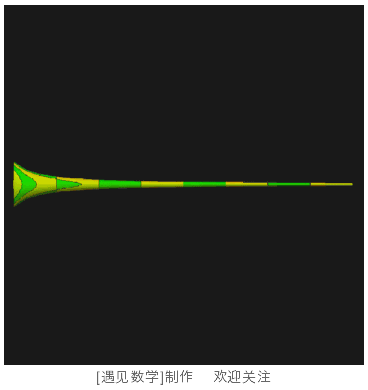
将这条曲线绕着 x 轴旋转一圈,就可以得到图 103 中的图形。
图 103 托里拆利小号
图中呈现的只是这个图形的一部分,理论上这是一个无限延伸的图形。这个图形已经不太像茶杯,更像是一个小号。数学上将这个特殊的形状命名为“托里拆利小号”,以纪念其发现者——意大利数学家托里拆利。
这个图形的特点为体积有限,而表面积无限。大家能从图中体会到这一点吗?或许会略微有一些难度吧。
下面我们就来分析一下这个图形。
首先,来看一下它的体积。换言之,就是当我们把这个小号立起来,从较宽的端口注满水时,水的注入量大概是多少。
计算体积
要计算出小号的体积,首先我们需要用一个与 x 轴垂直的平面沿x 轴纵向切开小号。所得到的截面就是一个近似于图 104 的图形。
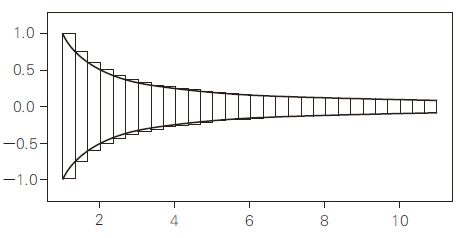
图 104 小号截面的近似图形
这个图形就像是由无数细长的长方形组合而成的,并且这些长方形的长度是不断递减的。将这个图形旋转一周,同样可以得到无数个薄薄的小圆板。
再进一步,我们还可以如图 105 那样,将截面分割得更加精细。
之后,再将此图形绕 x 轴旋转一周,就可以得到对应的无数个小圆板。此时,所有这些小圆板的体积之和,就非常接近于我们所求的小号的体积了。而如果要进行更精确的计算,则要切割得足够细, 使这些小长方形的宽度足够小,小到整个图形无限近似于小号截面时,就可以得出小号体积的正确答案了。
图 105 切割得更精细!
有了明确的操作方法,接下来我们就可以试着去动手计算。
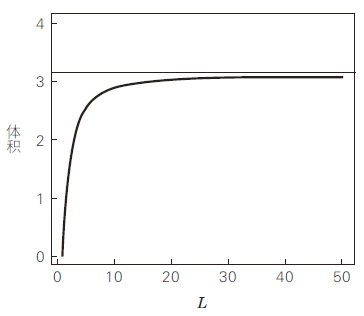
首先,假设小号的长度为 L -1,那么要计算小号的体积,就是要计算 x 从 1 到 L 时的体积。根据 L 与小号体积的变化情况,可以绘出如图 106 所示的曲线。
图 106 长度从 1 到 L 时小号体积的相应变化
小号在长度方向上是无限延展的。而随着长度 L 的不断增大,体积的增加幅度却不断放缓。那么,不管长度有多长,可以肯定的是, 小号的体积是无法超过某一个特定的数字的。
数学家们根据详细计算已经发现,长度无线延展的托里拆利小号,其体积最终等于π 。
表面积真的是无限吗?
计算完了体积,下一步我们要探讨的就是小号的表面积了。这次,我们需要更精确地截取小号的近似截面。
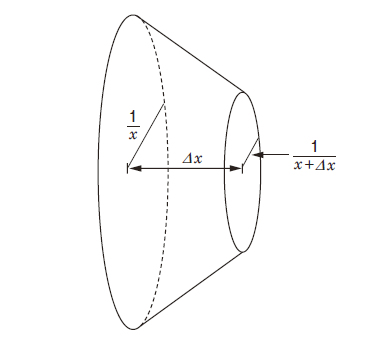
如图 107,直接截取小号从 x 到 Dx 的一段,得到一个类似圆锥台(将圆锥的顶端整齐切除后得到的立体图形)的图形。
图 107 将托里拆利小号按照厚度 Dx 进行截取
以上仅是一个近似的示意图,如果能够将 △x 的值缩小,那么把所有这些切割出的圆锥台的表面积相加,不就可以得出托里拆利小号的表面积了吗 ?
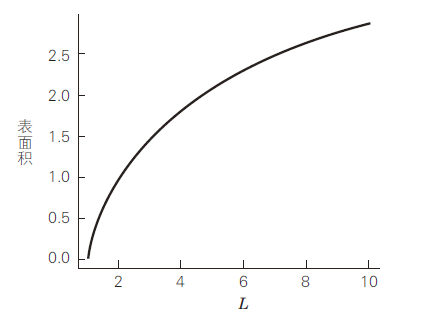
依照这个思路,我们来计算 x 从 1 到 L 变化时小号的表面积, 用图 108 的曲线表示。
图 108 小号的表面积
可以看到,与图 106 的曲线,也就是小号体积随长度变化的曲线相比,随着长度的增加,表面积增长的幅度更为剧烈。不过,从这个结果也还是无法明确得出小号的表面积是否真的是无限大。
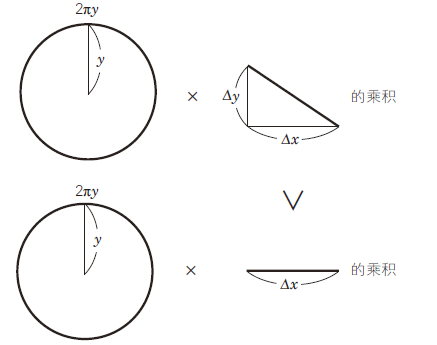
在这种情况下,就需要我们将小号表面积的计算进行更为精细的拆解。如图 109 上方的图形所示,可以用半径为 y 的圆的周长2 πy,再乘以圆锥台的斜面的长(斜长),计算出单个圆锥台的表面积,然后将所有圆锥台的表面积相加,就可以得出小号的表面积。
图 109 由下方的乘积来界定表面积
在这里,圆锥台斜面的长虽然是未知的,但我们可以肯定的是, 这个值一定大于圆锥台的厚度 △x 。由此可知,小号的表面积也应当大于“圆的周长(2πy )乘以 △x 的值”。
更明确的表述为,小号的表面积大于2πy × △x 。
那么,此时问题就可以替换一下了,即求 2πy × △x 的值是多少。
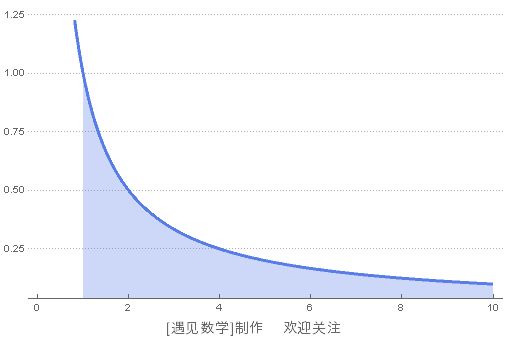
当 △x 足够小时,这个乘积就可以用图 110 的反比例函数的面积再乘以2π 来表示。
图 110 小号表面积大于图中灰色部分面积乘以 2π 所得的值
反比例函数的面积是无限大的。从 1 到 L 的面积,可以用以下公式来表述:
log L
log 在这里可以大致理解为一个和 L 的位数成比例增长的函数。如果 L 是无限大的,那么 logL 的值也是无限大的。
即使小号的长度(L -1)是有限的,当 L 越来越大时,体积也会逐渐接近于一个特定的值,但表面积却是无限增大的。表面积无限大也就意味着,若想制造这样一个物体,则原材料永远也无法满足消耗。
本节中我们探讨了一个架空的问题——无限长的小号,但是现实世界里有些物理现象的性质与该问题是存在关系的。例如,我们都知道日本列岛的面积是有限的。但是海岸线的长度呢?翻开日本地图,粗略一看,会感觉海岸线长度是可以计算的有限数值,但是深入探究、细致测量的话,就会发现这个值越来越大,最终竟会出现数值趋向于无限大的情况。
海岸线的例子和面积、体积都无关。放在这里只是想告诉大家, 小号的例子、海岸线的例子都说明了一个道理:“有限的世界中潜藏着无限”。
还有很多例子都可以印证这一点。所谓“无限”,不仅仅是研究者想象出的架空的产物,而是实际存在的一种现象。(完)