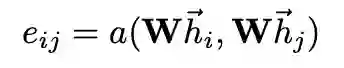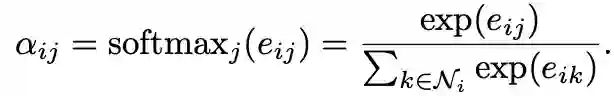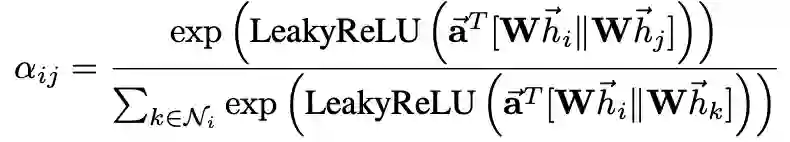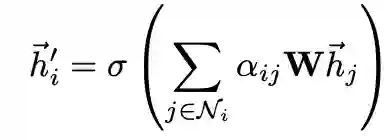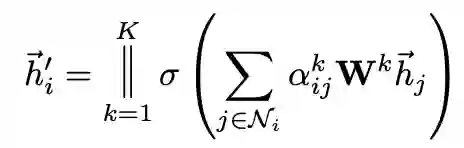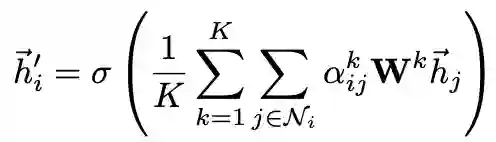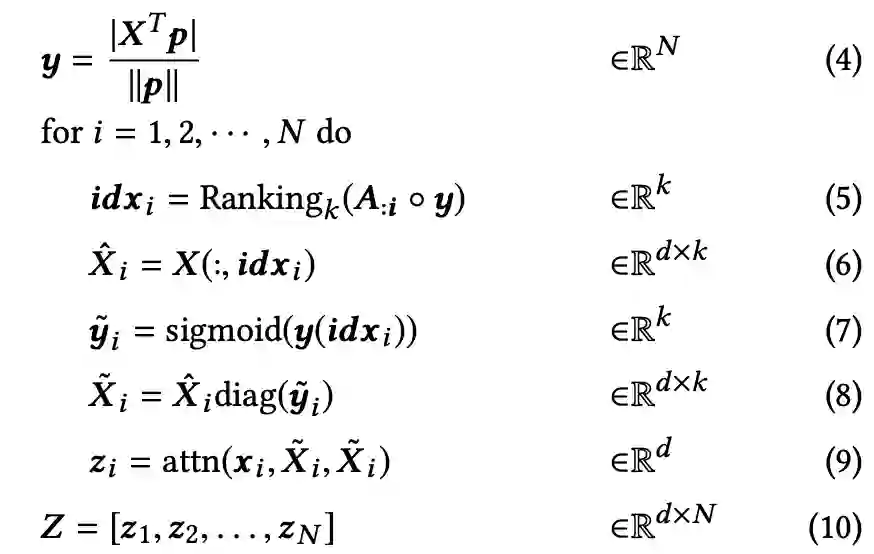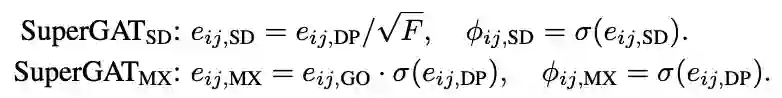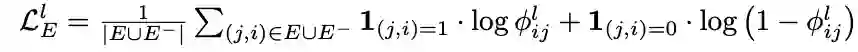论文小综 | Attention in Graph Neural Networks

2021 年 5 月 10 日 图与推荐

本文作者：方尹、杨海宏，浙江大学在读博士，主要研究方向为图表示学习

近年来，图卷积神经网络(Graph Convolutional Network, GCN)利用图卷积从图结构数据中提取特征，成功应用于节点分类、图分类、链接预测等任务，用途广泛。GCN在一系列任务中取得突破性进展的同时，其局限性也被放大：GCN擅长处理transductive任务（训练与测试阶段都基于同样的数据），但难以完成inductive任务（训练与测试阶段需要处理的数据不同，通常训练阶段在子图上进行，测试阶段需处理未知的节点）；难以处理有向图，不易实现将不同的学习权重分配给不同的邻居节点。

Graph Attention Networks

发表会议：ICLR 2018

Motivation:

针对上述问题，本文在GCN中引入注意力机制，提出了Graph Attention Networks (GAT)。GAT允许处理不同大小的输入，通过关注输入中与任务最相关的部分来做出决策。本质上，GAT有两种运算方式，分别为global graph attention和mask graph attention.由于global graph attention方式中每一个节点对于图上任意节点都进行attention运算，相当于丢弃了图结构这个特征，且面临高昂的计算成本，因此作者在文中采用mask attention，即注意力的运算只在邻居节点之间进行。

Model:

与所有注意力机制一样，GAT的计算分为两步。

第一步：计算注意力系数(attention coefficient)

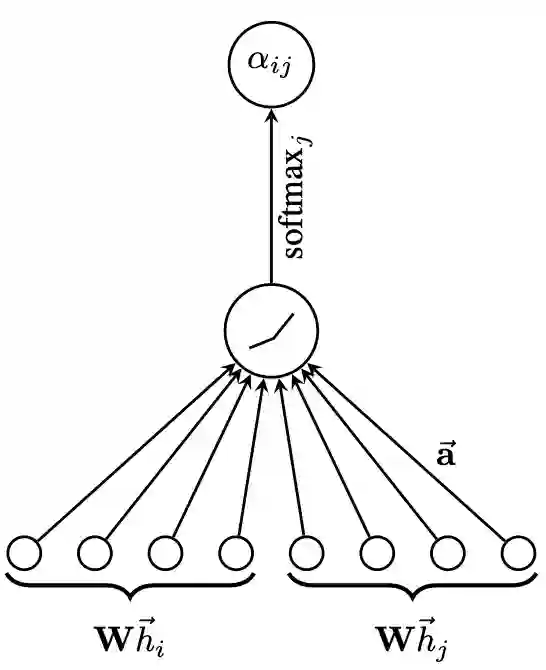
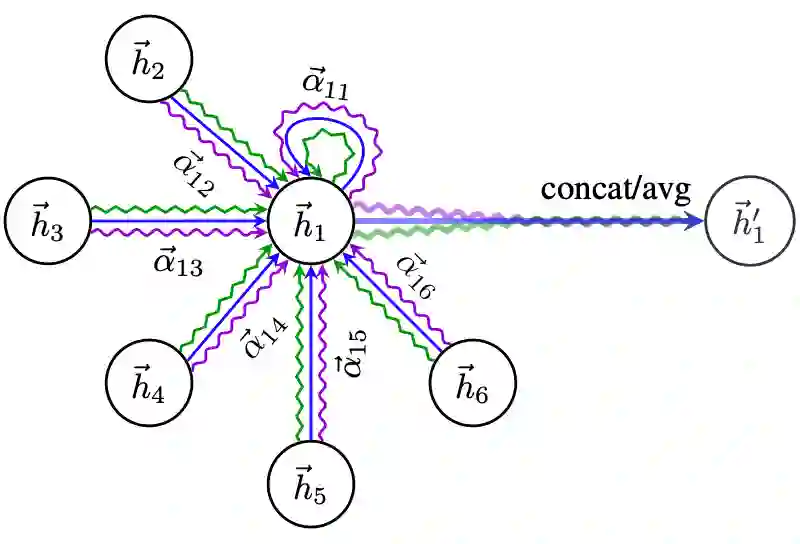
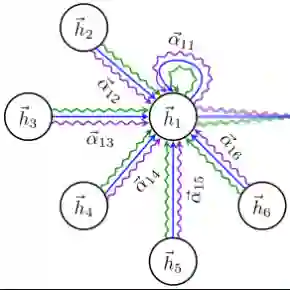
首先每个节点的输入特征向量，通过共享参数的线性变换进行特征增强。对于任意节点i，计算其与任意邻居节点j的特征之间的注意力系数：

为了使不同节点之间的注意力系数易于比较，通过softmax进行归一化处理：

具体实现方法如下：

第二步：加权求和(aggregate)

归一化的注意力系数被用于对特征加权求和，作为每个节点的最终输出特征：

为增加训练过程的稳定性，可使用multi-head并行计算K个分支，最后对所有分支的计算结果拼接或求均值：

与GCN不同，GAT允许隐式地为同一节点的邻居分配不同的重要性，同时学到的注意力有助于模型的可解释性。GAT的运算方式是逐点运算，不必预先访问全局图结构，适用于inductive任务。不要求图是无向的，如果边j→i不存在，只需省略 $\alpha_{ij}$ .

Experiment:

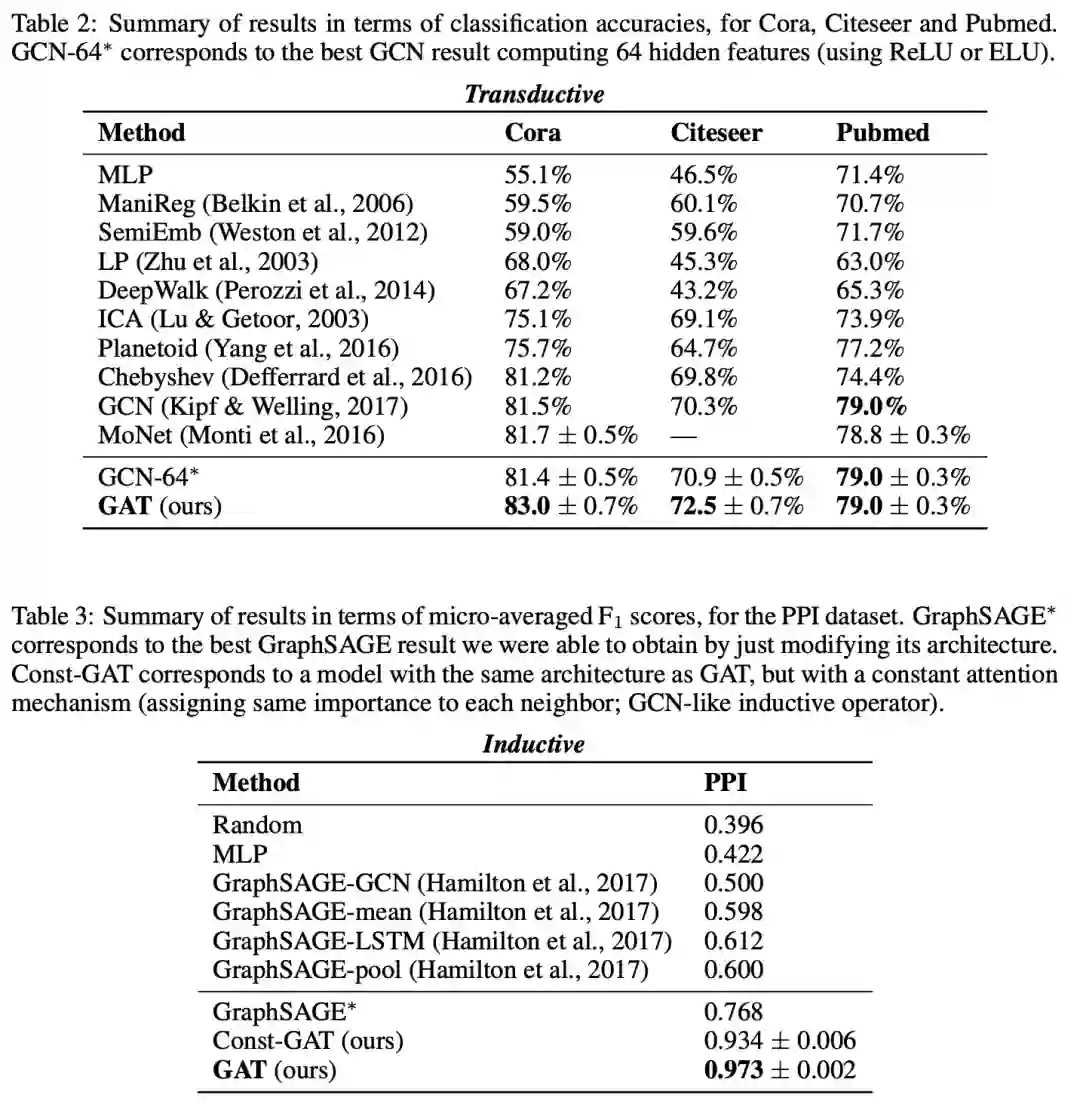
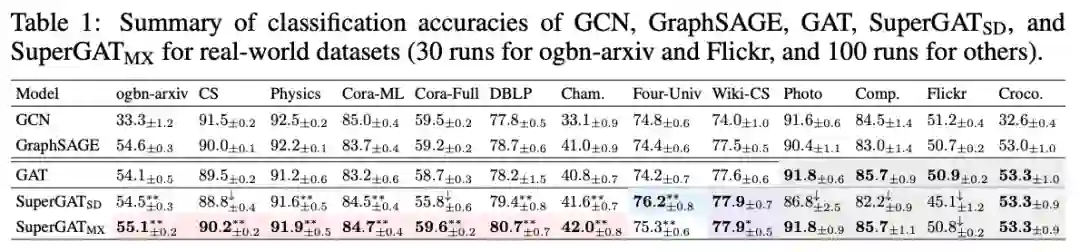
如上表所示，GAT分别在transductive和inductive任务上超越了GCN和GraphSAGE.

Graph Representation Learning via Hard and Channel-Wise Attention Networks

发表会议：KDD 2019

Motivation:

当图中含有大量节点时，graph attention operators(GAOs)会消耗大量的计算资源，包括计算成本和内存使用量。此外，GAO使用soft attention operator，计算图中所有相邻节点的信息。为了在大规模图数据中应用注意力机制，文中提出将硬注意力机制(hard graph attention operator, hGAO)引入GAOs来减少计算量。如果直接在图结构数据上使用hard attention仍会消耗大量计算资源。因此改进的hGAO对邻居节点进行筛选，保留部分邻居参与计算。

Model:

本文使用一个可训练的投影向量p，将特征矩阵X投影到N维向量空间中，y代表每个节点的重要性程度(4)。根据每个邻居节点的重要性程度进行排序，选择k个投影值最大的节点(5)。根据选出的idx，选择新的节点信息(6)。使用门操作来控制信息流，通过将sigmoid函数应用于选定的投影值来获得门向量(7)。通过矩阵乘法控制选定节点的信息(8)，在通过注意力机制，生成新的节点信息。

hGAO能够减少时间复杂度，但因涉及到了邻接矩阵的操作，依然会有和GAO一样的空间复杂度。作者提出利用channel-wise graph attention operator(cGAO)，只考虑节点本身的信息而不考虑邻接矩阵的信息来减少空间复杂度。将特征矩阵X的每一行看作一个通道，即每一类特征都是一个通道。假设假设同一节点内的特征彼此关联，且不同节点内的特征之间没有关联。这意味着cGAO不需要邻接矩阵A提供的连通性信息，从而避免了对邻接矩阵的依赖。

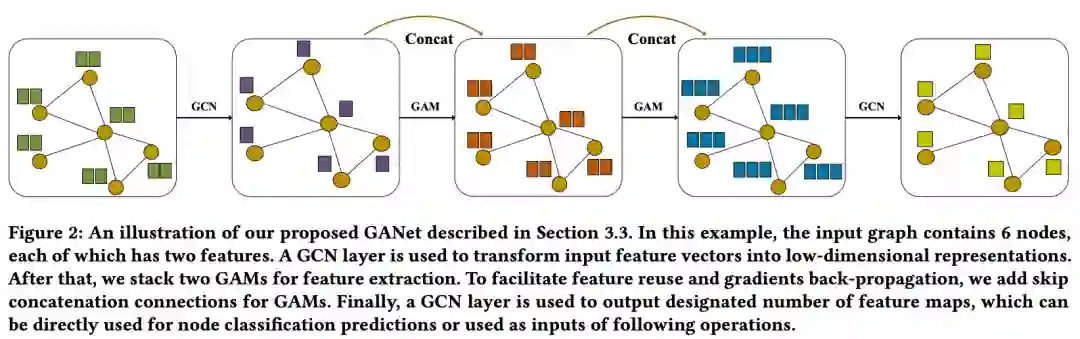
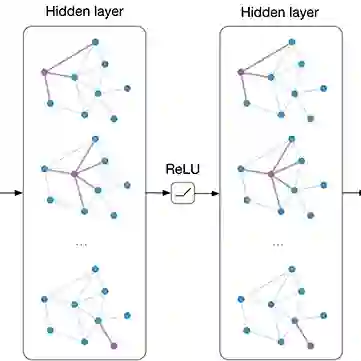
本文将hGAO和cGAO构建为GAM模块。如下图所示：

Experiment:

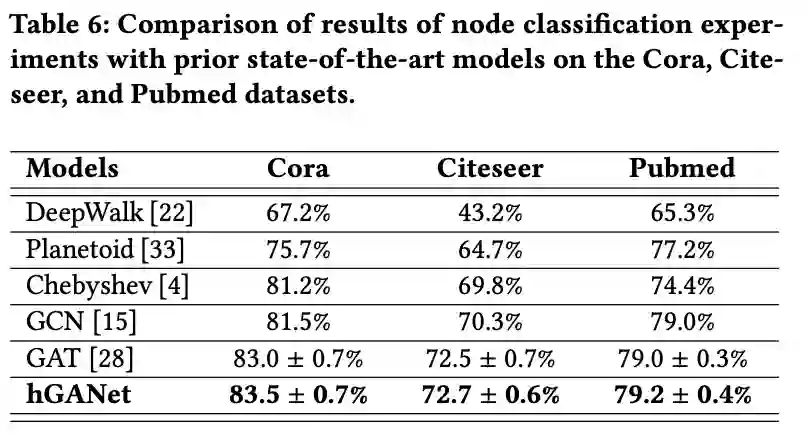
作者对比了GAO, hGAO和cGAO的计算效率。如下表所示：

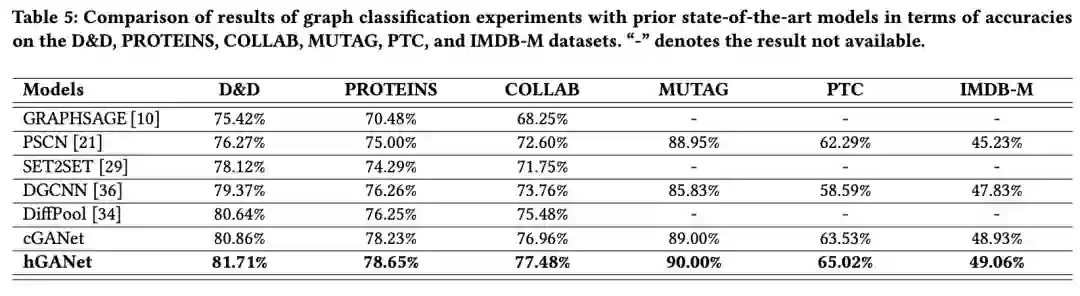
除此之外，hGANet分别在transductive和inductive任务上取得了不错的效果。

How to find your friendly neighborhood: Graph attention design with self-supervision

发表会议：ICLR 2021

Motivation:

GAT通过给不同的邻居节点分配不同的权重，从而使聚合的节点特征更加合理。但是当图中存在噪声时，会影响GAT的结果。本文通过提出两种对GAT的不同改进，来解决目前存在的问题。

Model:

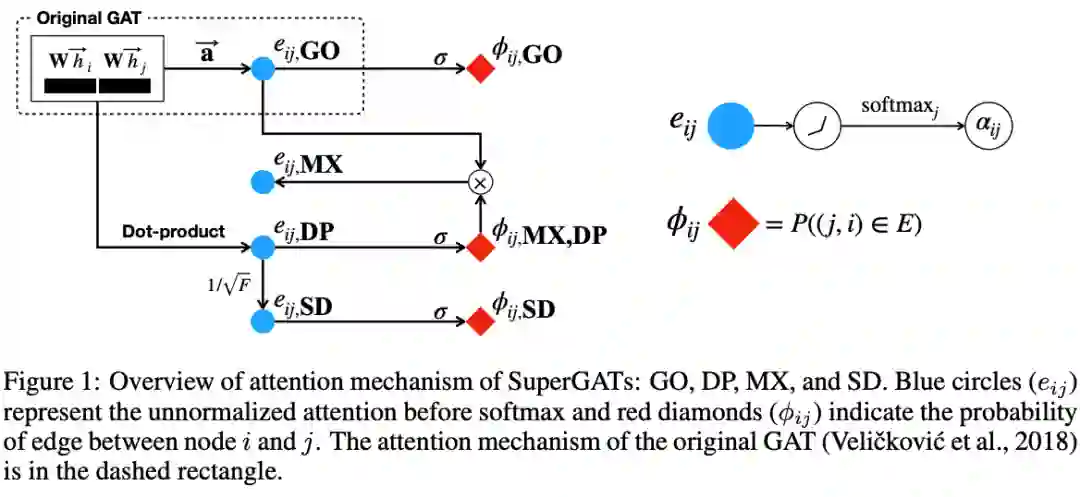
作者提出SuperGATs，旨在通过一个半监督的边预测任务来限制节点的特征向量。该函数预测了节点i和j之间存在边的概率：

本文提到了四个方法：GO(original GAT)、DP(dot-product attention)、SD(scaled dot-product)、MX(mixed GO and DP). GO为原始的GAT算法，DP将两个节点的特征向量相乘。SD和MX分别定义如下：

损失函数定义为：

其中，第一项是节点分类的交叉熵损失函数，最后一项是正则化项，中间一项代表着节点特征和两节点之间的边是否存在。将两节点的特征向量代入中，可以计算该边存在的概率。若两节点在真实图中不存在边，但计算出的存在边的概率很大，则损失很大。该项损失相当于通过图上已知的边关系，调整节点的特征向量。

Experiment:

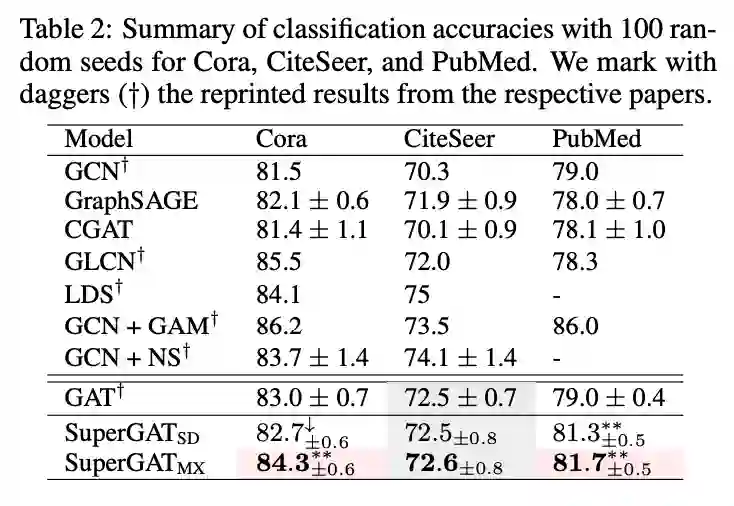
本文在多个真实数据集上进行了实验，结果表明SuperGAT获得了不错的效果。

综上所述，在注意力机制的作用下，图神经网络(Graph Neural Network, GNN)会关注到图中最重要的节点和节点中最重要的信息。受益于注意力机制，模型能够过滤噪音邻居，提升模型性能并对结果具有一定的可解释性。NLP中通常针对单独或整体的attention head，在attention weight上建立probe classifier，以研究模型真正关注到的部分。这样的方法后续也可以迁移到图结构数据上，对attention-based GNN进行解释。

未来还有更多潜在的方法和任务等待发掘，欢迎大家补充和交流。