【论文笔记】自注意力图池化
导读
近年来,提出了许多将深度学习应用于结构化数据(图)的方法,这些方法集中于在图数据中推广卷积神经网络的使用,包括在图中重新定义卷积与下采样(池化)操作。将卷积运算推广到图的方法已被证明是提高了性能的方法,并得到了广泛的应用。然而,在图上应用下采样的方法仍然有困难并且还有提高的空间。在本文中,我们提出了一个基于自注意力机制的图池化方法,可以同时考虑节点特征和图拓扑。

论文链接:
https://www.zhuanzhi.ai/paper/79bfee5566591aead9fdf779e3ac646a
动机
先前的图池化方法存在参数复杂(DIFFPooL)以及无法利用图拓扑结构信息(Graph u-net)的问题,因此,我们提出了SAGPool,它是一种在分层图池化的上下文中用于GNN的自注意力图池方法,同时可以以端到端的方式用更少的参数学习分层表示。
方法
SAGPool的核心是,使用一个GNN去产生自注意力分数,整体框架如下图所示:
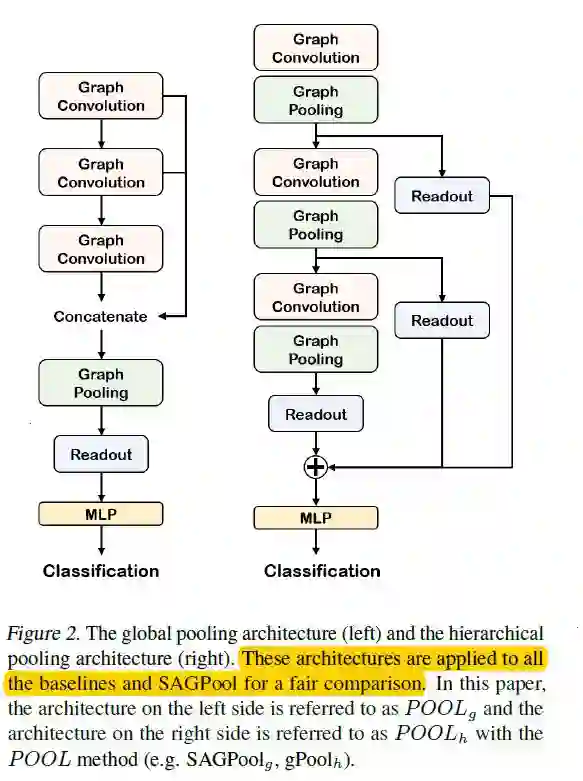
为了更好地确定模型的哪些修改有助于提高性能,我们分别采用全局池化和分层池化模型架构。
全局池化框架(左图),由三个图卷积层组成并且每一层的输出拼接在一起。节点特征被图池化层之后的readout层聚合。然后,将图形特征表示传递到线性层进行分类。
分层池化框架(右图):该体系结构由三块组成,每块由一个图形卷积层和一个图池化层组成。每个块的输出汇总在readout层中, 每个readout层的输出总和被馈送到线性层进行分类。
图卷积层
在该层可选择各种类型的图卷积,我们将Kipf&Welling提出的广泛使用的图卷积用于所有模型。
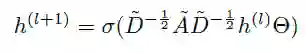
其中:
h^(l)是l层的节点表示
⊙∈R^{F×F'}是具有输入特征维度F与输出特征维度F‘的卷积权重
激活函数选择Relu函数
自注意力图池化层
我们提出的自注意力图池化层整体结构如下图所示,主要包括基于GCN的自注意力分数计算以及通过注意力分数进行图池化操作。
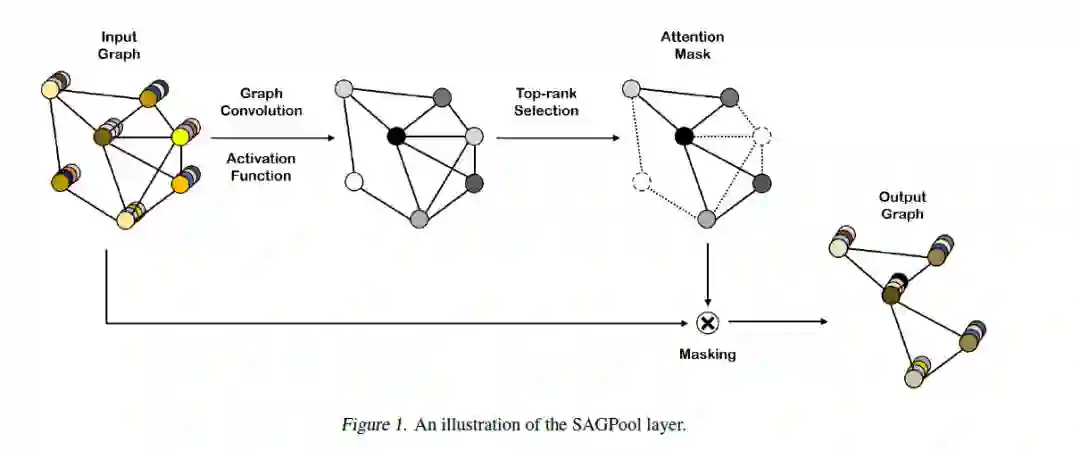
自注意力掩码(mask)
自注意力机制被广泛的应用于最近的研究中。这些机制使得可以分配更多的注意力在重要的特征,不那么关注不重要的特征。我们通过图卷积获得注意力得分。例如,若使用Kipf & Welling的图卷积公式,则自注意力得分Z∈R^{N×1}计算如下:
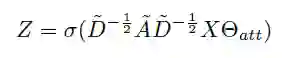
其中:
σ是激活函数
~A∈R^{N×N}是具有自连接的邻接矩阵(例如:~A=A+I_N)
~D∈R^{N×N}是~A的度矩阵
X∈R^{N×F}是具有N个节点与F维特征的图的输入特征
⊙_att∈R^{F×1}是SAGPool层唯一的参数
通过使用图卷积去获得自注意力分数,可以获得基于图特征和拓扑的结果。在得到注意力得分之后,我们采用Gao & Ji等人提出的节点选择方法,选择输入图中保留的节点。通过池化率k(k∈(0,1])来确定保留的节点数,具体计算如下:
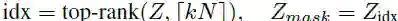
其中:
top-rank是返回[kN]中分数靠前的节点的索引
._idx是索引操作,Z_mask是特征注意力掩码
图池化
输入的图通过上文中提及的Masking操作处理之后,得到的要保留节点组成的新图的表示如下:
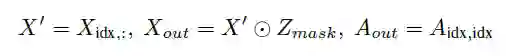
其中:
X_{idx,:}是在特征矩阵中通过idx逐行索引
⊙为按元素相乘
A_{idx,idx}是在特征矩阵中通过idx逐行、逐列索引
X_out与A_out是新的特征矩阵与相关的邻接矩阵
SAGPool的变体
若GNN采用节点特征与邻接矩阵作为输入,注意力分数Z∈R^{N×1}的的计算表示为:
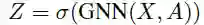
其中:
X表示节点特征,A表示邻接矩阵
通过选择不同的GNN进行自注意力分数的计算,我们可以得到不同的SAGPool的变体,下面介绍SAGPool的三种不同的变体SAGPool_augmentation、SAGPool_serial以及SAGPool_parallel。
SAGPool_augmentation:不仅使用相邻的节点,同时还使用多-hop连接节点来计算注意力分数。以2-hop为例,通过添加邻接矩阵的平方会在2—hop 邻居之间创建边,计算如下:
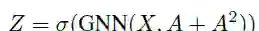
SAGPool_serial:GNN层的堆叠允许2—hop节点的间接聚集。在这种情况下,SAGPool层的非线性和参数数量会增加。
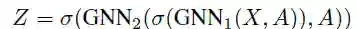
SAGPool_parallel:通过M个GNN获得的平均注意力得分如下:
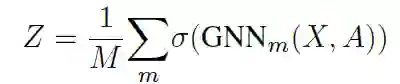
Readout 层
Readout层主要是用来聚合节点特征,以进行固定大小的表示,表示为:
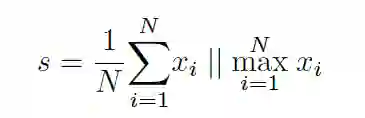
其中:
N是节点的数量
x_i是第i个节点的特征向量
‖表示拼接操作
实验
数据集
文中从基准数据集中选择了五个具有大量图形(> 1k)的数据集,并在训练数据中选择10%作为验证。表1汇总了数据集的统计信息。
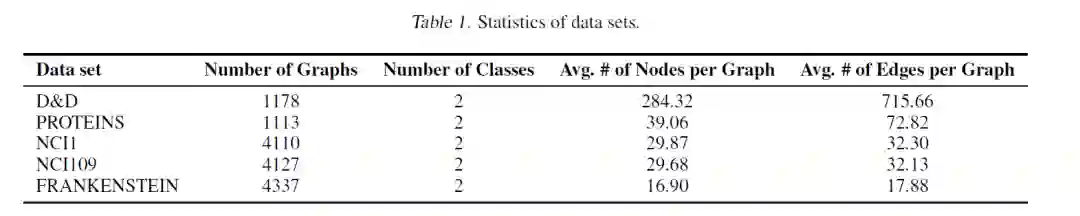
丨基准数据集涉及文章Kersting, K., Kriege, N. M., Morris, C., Mutzel, P.,and Neumann, M. Benchmark data sets for graph kernels, 2016.
D&D:包含蛋白质结构图,一个节点表示一个氨基酸并且两个节点之间的距离小于6°A,则存在边。标签表示蛋白质是酶还是非酶。
PROTEINS:依然是蛋白质的集合,其中节点是secondary结构元素。如果节点有边,所述节点是氨基酸序列或在封闭的3D空间中。
NCI:NCI(Wale等人,2008)是用于抗癌活性分类的生物学数据集。在数据集中,每个图形代表一种化学化合物,节点和边分别代表原子和化学键,包括NCI1与NCI109。
FRANKENSTEIN(Orsini等人,2015)是一组分子图(Costa&Grave,2010),其节点特征包含连续值。标签表示分子是诱变剂还是非诱变剂。
参数设置

实验结果
为了对比SAGPool与以往的模型的效果,文中使用了Set2Set, SortPool作为全局池化框架的baseline,同时使用DiffPool与gPool作为分层池化框架的baseline,对比结果如下所示:
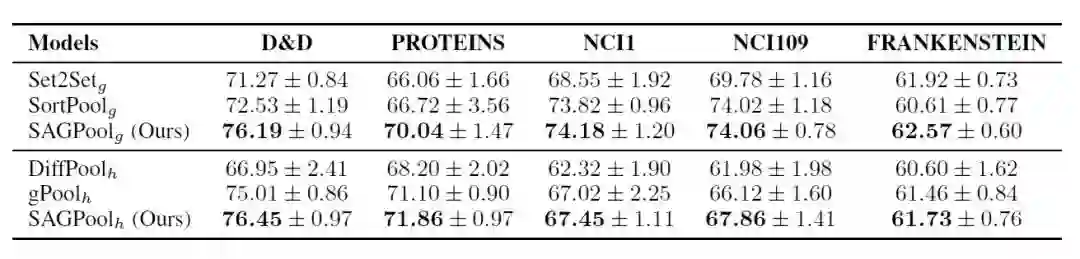
由于全局池体系结构最大程度地减少了信息丢失,因此它在节点(NCI1,NCI109,FRANKENSTEIN)较少的数据集上的性能优于分层池体系结构。但是,分层结构在具有大量节点(D&D,PROTEINS)的数据集上更为有效,因为它可以有效地从大规模图形中提取有用的信息。因此很难确定全局池体系结构或分层池体系结构是否完全有利于图分类。
同时文中还比较了上文提到的三种使用最广泛的GCN(SAGPoolCheb,SAGPoolSAGE,SAGPoolGAT)的性能,以及上文提到的肌酸注意力分数的SAGPool的三个变体的性能,结果如下所示:
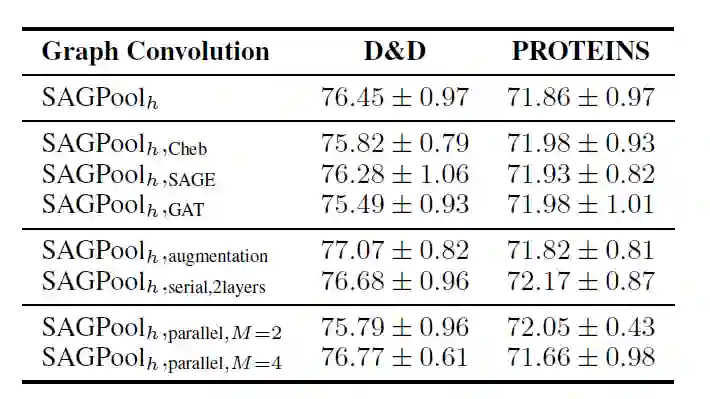
总结
SAGPool是一种基于自注意的新型图池化方法。具有以下特征:分层池化,同时考虑节点特征和图拓扑,合理的复杂性以及端到端表示学习。无论输入图形的大小如何,SAGPool都会使用一致数量的参数。