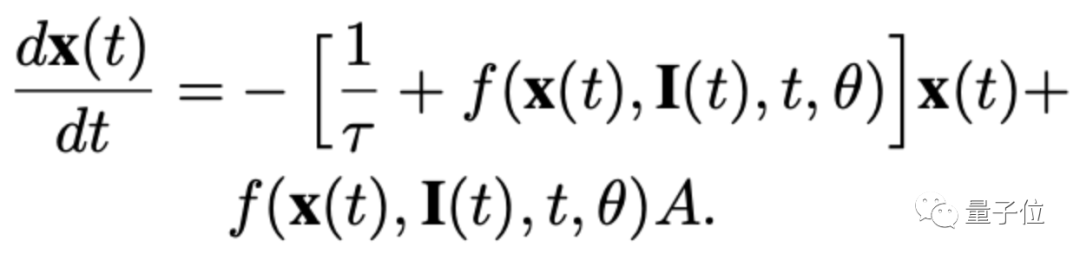百年微分方程难题被解决！神经元相互作用方式有了解析解描述，作者：可以模拟大脑动力学了 | MIT

Pine 萧箫 发自 凹非寺
量子位 | 公众号 QbitAI

困扰数学家百年的微分方程难题，被MIT解决了！

这个微分方程可以用来模拟神经元间通过突触的相互作用方式，换言之就是大脑传递信息的过程。现实生活中有诸多应用场景，比如自动驾驶、大脑和心脏的监测等。

然而，以前求解这个微分方程的过程比较复杂，计算量还会随着数据的增加而暴增——

模拟几个神经元之间的信息传递还好。但如果像人脑一样，有几百亿个神经元、几百万亿个突触呢？

现在，研究人员终于找到了这个微分方程的近似解析解，一下子将计算速度提升了好几倍。

要知道，论文第一作者表示，从1907年以来，就一直没有人能找到这个微分方程的解析解。

牵一发而动全身，论文第一作者还放话称：

由数十亿个神经元和数万亿个突触组成的大脑动力学，我们现在也可以模拟了！

还有网友表示：

这将会改善神经网络对大规模数据计算的适应能力。点个赞！

相关论文已发表在最新一期的Nature MI上，立刻引发了不少关注：

到底是什么样的一个数学难题，能够让网友产生这样大的反应，一起来看看~

解决了一个什么样的难题？

这次MIT的突破，在于找到了两个神经元之间通过突触相互作用微分方程的近似解析解。

突触，即一个神经元的冲动传到另一个神经元或另一细胞间的相互接触的结构。两个神经元之间神经冲动，则是由突触前末梢，传递给突触后神经元的。

要模拟神经元间通过突触相互作用的过程，就需要模拟传导的动作电位。

MIT研究人员先是用去年做出来的“液体”神经网络 （Liquid Time-constant Networks，简称LTC）模拟了这一现象。

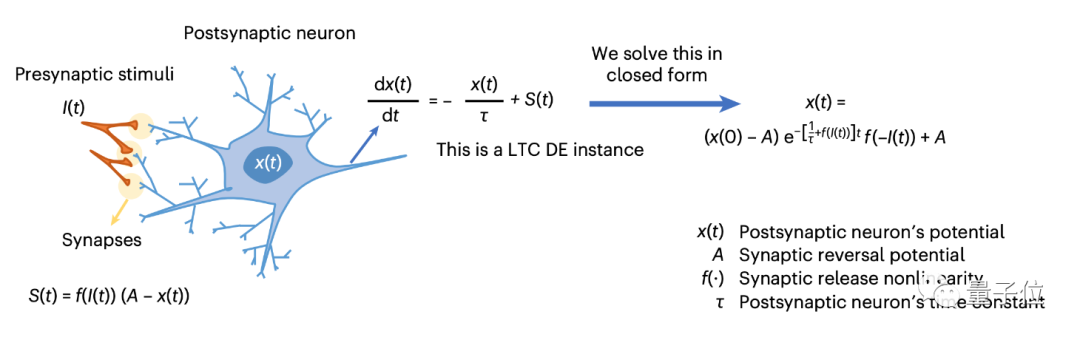
如下图，x(t)就是研究希望求解的突触后神经元电位，但之前它需要通过直接求解微分方程来计算，也就是图中左边的一大堆方程：

BUT，他们很快发现，LTC神经网络模型虽然模拟得好，但常微分方程（ODE）计算还是不够快，通常需要结合ODE求解器来搞定。

即通过左边的一堆公式，虽然在给定时间t的情况下也能算出x(t)来，但它不仅算得慢，而且误差还会随着求解过程中的迭代计算一步步被放大。

但如果能求出x(t)的解析解，也就是求出等式右边不包含x(t)这个变量的公式，那么计算效率就能得到成倍的提升。

然而，求解这个常微分方程dv/dt=−glv(t)+S(t)的方法，从1907年提出以来还没有人求出过它的解析解。

在通过一番计算后，研究人员终于得出了这个微分方程的近似解析解，能很好地近似出x(t)的数值：

最关键的是解析解能“一步到位”地求出结果，研究人员表示这比正常求微分方程模型快上1~5倍。

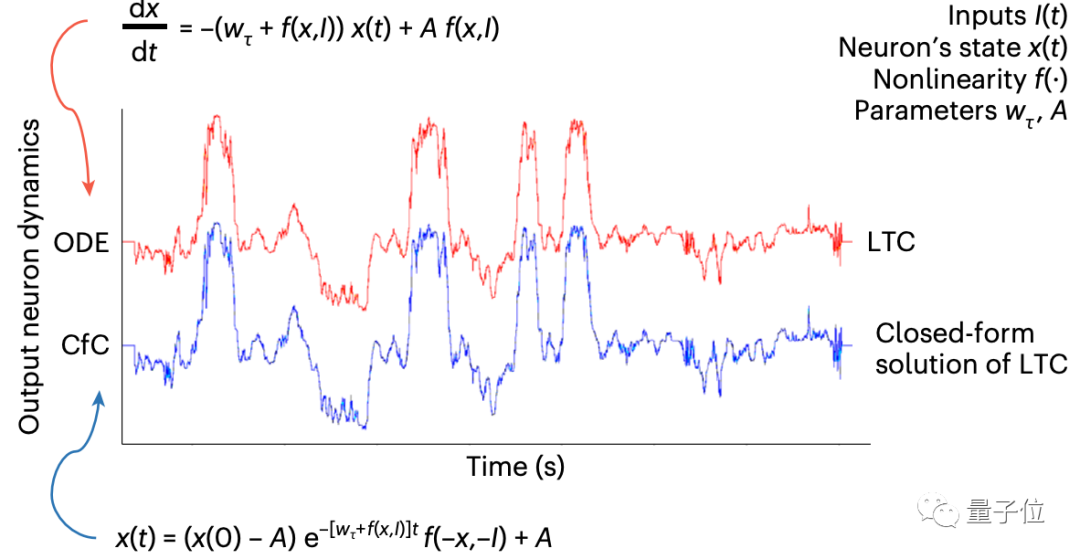
依靠这个新的近似解析解，研究人员提出了一种名叫CfC （closed-form continuous-depth networks，闭式连续深度神经网络）的模型，进一步提升了计算效率、降低了微分方程求解带来的近似误差（approximation error）。

求解出来与原微分方程的相似度也极高：

所以CfC的提出，究竟解决了什么问题？

作者：下一步建立大脑计算模型

提到CfC的作用，还得先说回它的基础，也就是MIT去年建立的“液体”神经网络（LTC）。

△图源：MIT

当时“液体”神经网络的提出，是用于简化如视频处理、金融数据和医疗诊断这类与连续时间强相关的问题计算。

这类问题往往与时间的相关度很高（如股票、视频等变量会不停地随着时间产生变化），这也导致它们的变化情况难以预测，往往需要求解非常复杂的偏微分方程。

“液体”神经网络就是为了解决这一点出现的，确实也提升了这类场景的计算效率。

然而，建立“液体”神经网络的灵感虽然来自小物种的大脑，具有很强的灵活性和适应能力，不过计算量仍然不算低——

一旦增加神经元和突触的数量，计算机可能就因为数据计算量过大“撑不住”了。

这不，今年MIT就带着CfC神经网络来了！

与“Liquid”神经网络相比，CfC可谓去粗取精，它既保留了“Liquid”网络的灵活、因果、稳定和可解释性，同时数量级更快、可扩展性更高。

换句话说，就是CfC更快更强了，而这也意味着它能够适用于更多任务。

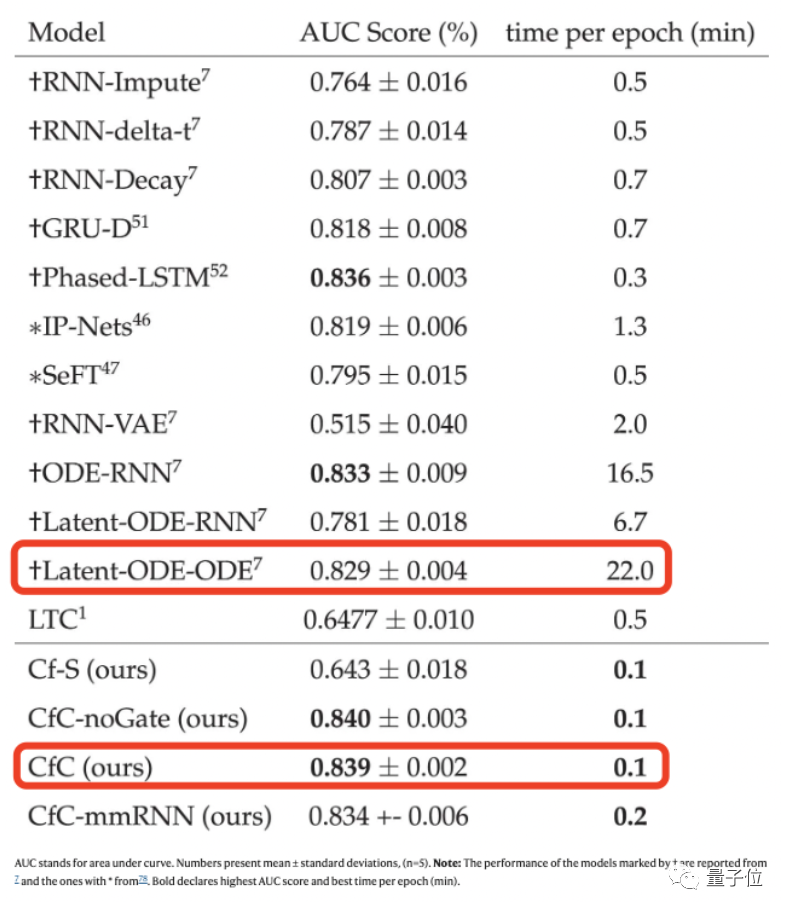
论文中的测试结果显示，CfC在一系列任务中表现都要优于SOTA神经网络。

比如说在一项医学预测任务中，对8000名患者进行抽样调查，新模型的速度要比连续潜伏模型快220倍。

其中，CfC在从运动传感器识别人类活动、建立模拟步行机器人的物理动力学模型以及基于事件的连续图像处理方面具有相当高的加速度和性能。

而这对应到现实的实际应用，就是无人驾驶、无人机导航或者各类预测任务。

值得一提的是，据MIT消息，此前也已有证据证明，CfC神经网络能够在没有额外学习的情况下将所学技能迁移到一个全新的环境中，这恰恰是人工智能研究最基本的挑战之一。

（没错，CfC也是不容小觑的）

这一步研究团队解决了神经元之间如何相互作用的描述，那下一步准备干啥？他们立了个flag：

希望通过测量数百万个神经元连接，建立大脑动力学模型。

论文的第一作者，同时也是MIT CSAIL研究所附属机构的Ramin Hasani也表示：

一旦我们对神经元和突触的联系有了一个解析解描述，我们就可以用数十亿个细胞建立大脑的计算模型了。

据神经学家估计，人脑神经元数量在1000亿个左右，不知道团队是否会挑战“模拟人类大脑”这一难题（手动狗头）。

目前CfC模型已经开源，想要拿它用来模拟一些问题计算的小伙伴，可以去看看了~

CfC项目地址：
https://github.com/raminmh/CfC

论文地址：
https://www.nature.com/articles/s42256-022-00556-7

— 完 —

「2022人工智能年度评选」火热报名中

仅剩7天，量子位「2022人工智能年度评选」即将截止报名！本次评选将从企业、人物、产品/解决方案三大维度设置5类奖项，抓紧时间参与吧！

更多关于评选标准、榜单报名欢迎扫描下方二维码～

点这里关注我 👇 记得标星噢 ~

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见 ~