北京大学NeurIPS 2021 | 用简单的梯度下降算法逃离鞍点

2021 年 12 月 6 日 专知

关键词：非凸优化，鞍点，梯度下降

导读

本文是 NeurIPS 2021入选论文《用简单的梯度下降算法逃离鞍点（Escape saddle points by a simple gradient-descent based algorithm）》的解读。该工作由北京大学前沿计算研究中心李彤阳课题组完成，探讨了优化理论中的一个重要问题：如何设计简单的、单循环结构的优化算法，使其可以有理论保证地逃离非凸目标函数中的鞍点。

论文地址：

https://www.zhuanzhi.ai/paper/17716f81bcda168a7670f32bc328de55

问题介绍

非凸优化（nonconvex optimization）是优化理论的核心研究领域之一，因为许多前沿机器学习问题都具有非凸的损失函数，包括深度神经网络、主成分分析、张量分解等。在最坏的情况下，找到非凸函数的全局最小值属于 NP-hard 问题。不过最近的许多实证与理论工作都表明，对于大量有着广泛应用的机器学习问题，所有局部最小值几乎都与全局最小值相等。因此，许多理论工作专注于寻找局部最优解而不是全局最优解。在这些工作中，鞍点成为了设计算法的主要障碍，因为高维的非凸目标函数可能含有大量鞍点，且它们往往具有远大于全局最优解的函数值。

因此，逃离鞍点是非凸优化理论中最重要的问题之一。具体来说，对于二阶可导的 $n$ 维函数 $f$ ，我们的目标是找到一个 $\epsilon$ 近似的局部最优解。近期的实证研究表明，现实世界中复杂的机器学习问题往往可以被简单的算法有效解决，这些算法在实践中也可以更容易地实现与维护。与之相反，具有嵌套循环结构的优化算法在问题规模增长时往往具有较大的开销，或存在调参不便、数值稳定性较弱等问题，使它们较难找到实际应用。出于这一考量，现有的逃离鞍点的研究多聚焦于开发基于梯度下降的，具有单循环结构的简单优化算法。在本文之前，最先进的算法为 Jin 等人提出的扰动加速梯度下降算法（perturbed accelerated gradient descent, PAGD），它可以在 $\widetilde{O}(\log^6{n/\epsilon^{1.75}})$ 次循环内找到一个 $\epsilon$ 近似的局部最优解。

主要结果

我们的主要结果是开发了一个基于梯度下降的，具有单循环结构的简单优化算法，它可以在 $\widetilde{O}(\log{n/\epsilon^{1.75}})$ 次循环内找到一个 $\epsilon$ 近似的局部最优解。与之前最先进的算法相比，我们的算法在 $\log{n}$ 这一项上实现了多项式加速。

现有文献的结果：

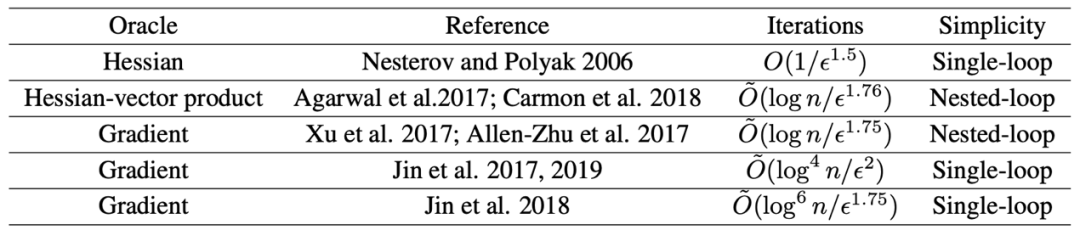
本文的结果：

我们也利用数值实验将本文的算法（ANCGD）与扰动加速梯度下降算法（PAGD）进行了对比。

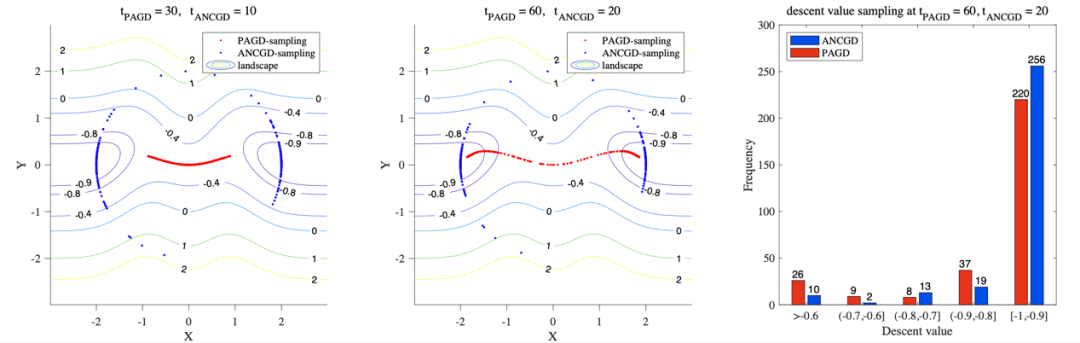
在该实验中，我们在左图所示的相同非凸函数上分别多次运行我们的算法（ANCGD）与扰动加速梯度下降（PAGD），其中蓝色点表示 ANCGD 的 samples 在10或20次迭代后的位置，红色点表示 PAGD 的 samples 在30或60次迭代后的位置。可以看出，即使在较少的迭代次数下，ANCGD 也有更好的收敛性。右图展示了 ANCGD 与 PAGD 的 samples 分别在20或60次迭代后，函数值的下降量。

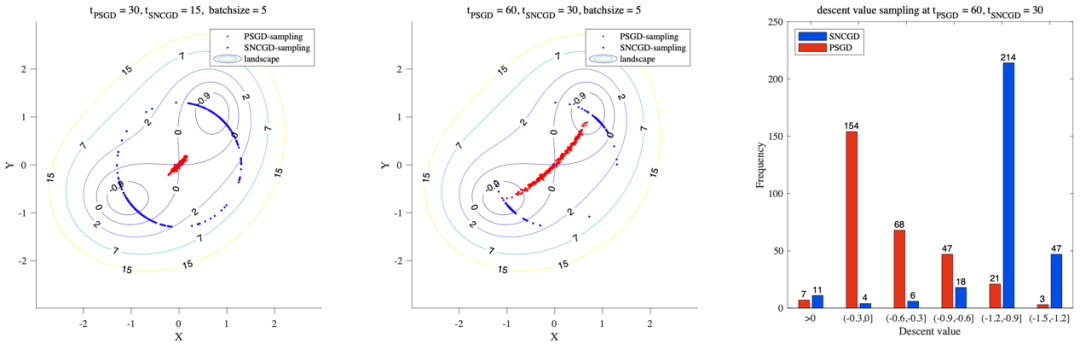
进一步地，我们把这一结果扩展到了随机梯度下降的情况中，并证明了我们的算法在这一设定下可以在 $\widetilde{O}(\log^2{n/\epsilon^4})$ 次循环内找到一个 $\epsilon$ 近似的局部最优解，并进行了如下的数值试验：

在该实验中，我们在左图所示的相同非凸函数上分别多次运行我们的算法（SNCGD）与扰动随机梯度下降（PSGD），其中蓝色点表示 SNCGD 的 samples 在15或30次迭代后的位置，红色点表示 PSGD 的 samples 在30或60次迭代后的位置。可以看出，即使在较少的迭代次数下，SNCGD 也有更好的收敛性。右图展示了 SNCGD 与 PSGD 的 samples 分别在30或60次迭代后，函数值的下降量。

方法和技术创新

本文之前，最有效的逃离鞍点的单循环算法，即扰动加速梯度下降算法（PAGD）由 Jin 等人提出。这一算法的基本思想十分简洁：在梯度较大的区域，利用 Nesterov 提出的加速梯度下降（AGD）进行迭代。若到达鞍点附近梯度很小、AGD 迭代效率很低的区域，则进行一次扰动，以期令现有迭代值离开鞍点附近。Jin 等人证明了在合理的模长设定下，各向同性的均匀扰动可以实现这一效果：只要在该扰动后再进行一定次数的 AGD 迭代，就能以一个很高的概率离开鞍点。

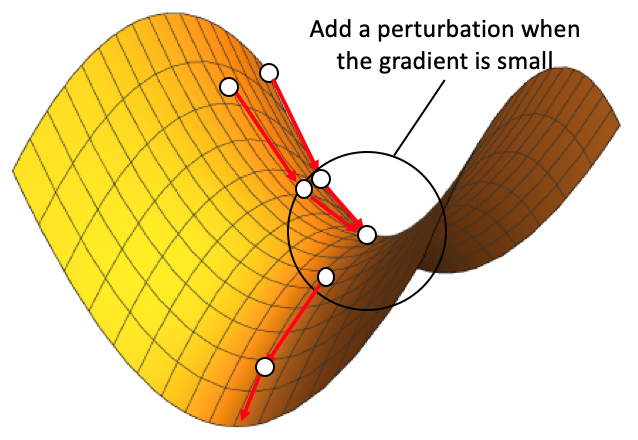
然而，均匀扰动仍然是较为低效的，它是在无法直接读取二阶 Hessian 矩阵这一限定条件下的折中。从直觉上，沿着鞍点附近的负曲率方向的定向扰动，会远比均匀扰动高效，特别是在函数维度较高时。在本文中我们观察到，我们可以在不计算 Hessian 矩阵的情况下，找到鞍点附近的负曲率方向。具体来说，我们把视角局限在鞍点附近的一个小区域中，该区域的函数值可以被近似视为一个二次函数。在这一小区域内，我们加入一个抖动并进行一定次数的 AGD 迭代，并在每次迭代后进行归一化，从而保证 AGD 迭代始终保持在这一小区域内。

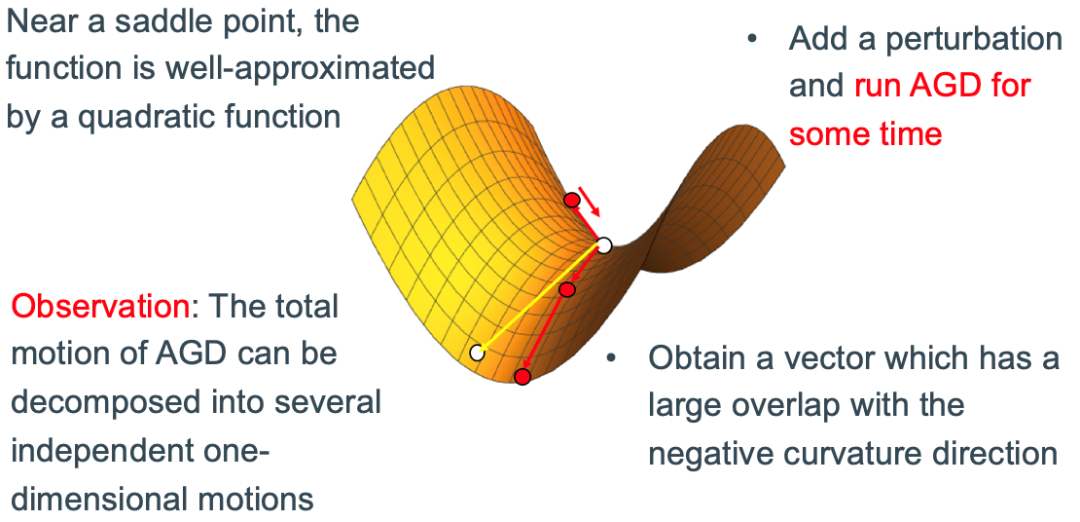
我们进一步证明，这样的 AGD 迭代可以被视作 $n$ 个互不干扰的一维 AGD 叠加。而且在至多 $\widetilde{O}(log\ n{/\epsilon^{1/4}})$ 次迭代后，我们可以得到一个位移矢量，其与鞍点的负曲率方向有很大的重合。进一步地，我们可以沿着这个位移矢量的方向加入定向扰动，使函数值下降至少 $\Omega(\epsilon^{3/2})$ ，从而更加有效地离开鞍点。

在随机优化的设定下，即使只能获得随机梯度值而无法获得准确梯度值，这一方法仍有很好的效果。

参考文献

[1] Naman Agarwal, Zeyuan Allen-Zhu, Brian Bullins, Elad Hazan, and Tengyu Ma (2017). "Finding approximate local minima faster than gradient descent". In: 49th Annual ACM SIGACT Symposium on Theory of Computing, pp. 1195–1199.

[2] Zeyuan Allen-Zhu and Yuanzhi Li (2018). "Neon2: Finding local minima via first-order oracles". In: Neural Information Processing Systems, pp. 3716–3726.

[3] Yair Carmon, John C. Duchi, Oliver Hinder, and Aaron Sidford (2018). "Accelerated methods for nonconvex optimization". In: SIAM Journal on Optimization 28 (2018), no.2, 1751–1772.

[4] Chi Jin, Praneeth Netrapalli, Rong Ge, Sham M Kakade, and Michael I. Jordan. (2021). "On nonconvex optimization for machine learning: Gradients, stochasticity, and saddle points". In: Journal of the ACM (JACM) 68, no.2, 1–29.

[5] Chi Jin, Praneeth Netrapalli, and Michael I. Jordan. (2018). "Accelerated gradient descent escapes saddle points faster than gradient descent". In: Conference on Learning Theory, pp. 1042–1085.

[6] Yurii Nesterov and Boris T. Polyak. (2006). "Cubic regularization of Newton method and its global performance". In: Mathematical Programming 108, no. 1, 177–205.

[7] Yi Xu, Rong Jin, and Tianbao Yang. (2017). "Accelerated gradient methods for extracting negative curvature for non-convex optimization".

专知便捷查看