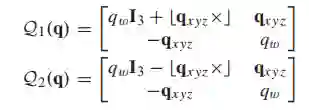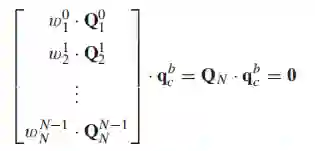VINS_Mono中camera-imu的旋转外参标定

2019 年 11 月 26 日 计算机视觉life

点击上方“计算机视觉life”，选择“星标”

快速获得最新干货

众所周知，VINS_Mono是一种融合了视觉和惯导这两种传感器的viSLAM系统，而视觉和惯导的融合可以带来1+1>2的效果，其优点如下：

可以借助IMU较高的采样频率，进而提高系统输出频率
可以提高视觉鲁棒性
可以有效消除IMU预积分的漂移
能够矫正IMU的Bias
可以解决视觉单目尺度不可观的问题

但是，为了使这个两个传感器融合，我们首先需要做的事情是将两个传感器的数据对齐，除了时间上的对齐，还有空间上的对齐。空间上的对齐通俗的讲就是将一个传感器获取的数据统一到另一个传感器的坐标系中，其关键在于确定这两个传感器之前的外参，本文将详细介绍VINS_Mono中camera-imu的旋转外参标定算法原理并对其代码进行解读。

相机与 IMU 之间的相对旋转

上图表示相机和IMU集成的系统从到的运动，其中视觉可以通过特征匹配求得到时刻的旋转增量，同时IMU也可以通过积分得到到时刻的旋转增量，设相机和IMU之间的旋转矩阵为，那么对任意时刻，满足：

将上式用四元数表示：

其中：

对于对相对旋转的测量值，可得过约束的线性方程：

在标定成功前，会一直增长，为了更好的处理可能存在的异常值，每个都乘以了一个类似于huber核函数的权重。对进行svd分解，其中最小奇异值对应的右奇异向量便为结果。

怎么确定标定成功的终止条件?

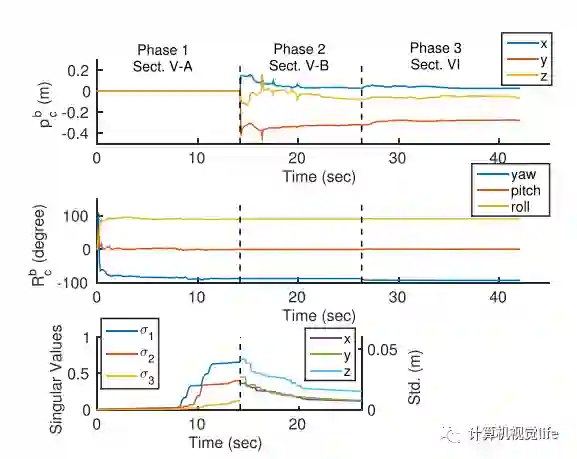
对于等式，由于camera-imu的外参是一个固定的值，即只有一个值，也就是说的零空间非零解存在一组。在足够多的旋转运动中，我们可以很好的估计出相对旋转，这时对应一个准确解，且其零空间的秩为1。但是在标定过程中，某些轴向上可能存在退化运动(如匀速运动)，这时的零空间的秩会大于1。判断条件就是的第二小的奇异值是否大于某个阈值，若大于则其零空间的秩为1，标定成功；反之秩大于1，相对旋转的精度不够，标定不成功。阈值为什么选取的是0.25，在文章《Monocular Visual–Inertial State Estimation With Online Initialization and Camera–IMU Extrinsic Calibration》中对随着奇异值的变化求得外参对这个系统的影响做了分析，如下图。

从图中可以看到，随着的增长，当接近0.1的时候，相机和IMU之间的相对旋转逐渐趋于一个稳定的值，此时求得的特征点的位置的精度已经达到5cm以内了。

对应代码及注释

//标定外参的旋转矩阵
//传入的参数是两帧间对应的3d点以及两帧间imu的积分量
bool InitialEXRotation::CalibrationExRotation(vector<pair<Vector3d, Vector3d>> corres, Quaterniond delta_q_imu, Matrix3d &calib_ric_result)
{
    frame_count++;
    Rc.push_back(solveRelativeR(corres));//帧间cam的R，由对极几何得到
    Rimu.push_back(delta_q_imu.toRotationMatrix());//帧间IMU的R，由IMU预积分得到
    Rc_g.push_back(ric.inverse() * delta_q_imu * ric);//将imu预积分转换到相机坐标系

    Eigen::MatrixXd A(frame_count * 4, 4);
    A.setZero();
    int sum_ok = 0;
    for (int i = 1; i <= frame_count; i++)
    {
        Quaterniond r1(Rc[i]);
        Quaterniond r2(Rc_g[i]);

        double angular_distance = 180 / M_PI * r1.angularDistance(r2);
        //A.angularDistance(B):是求两个旋转之间的角度差，用弧度表示
        ROS_DEBUG(
            "%d %f", i, angular_distance);

        //huber核函数做加权
        double huber = angular_distance > 5.0 ? 5.0 / angular_distance : 1.0;
        ++sum_ok;
        Matrix4d L, R;

        //R_bk+1^bk * R_c^b = R_c^b * R_ck+1^ck
        //[Q1(q_bk+1^bk) - Q2(q_ck+1^ck)] * q_c^b = 0
        //L R 分别为左乘和右乘矩阵
        double w = Quaterniond(Rc[i]).w();
        Vector3d q = Quaterniond(Rc[i]).vec();
        L.block<3, 3>(0, 0) = w * Matrix3d::Identity() + Utility::skewSymmetric(q);
        L.block<3, 1>(0, 3) = q;
        L.block<1, 3>(3, 0) = -q.transpose();
        L(3, 3) = w;

        Quaterniond R_ij(Rimu[i]);
        w = R_ij.w();
        q = R_ij.vec();
        R.block<3, 3>(0, 0) = w * Matrix3d::Identity() - Utility::skewSymmetric(q);
        R.block<3, 1>(0, 3) = q;
        R.block<1, 3>(3, 0) = -q.transpose();
        R(3, 3) = w;

        A.block<4, 4>((i - 1) * 4, 0) = huber * (L - R);
    }

    //svd分解中最小奇异值对应的右奇异向量作为旋转四元数
    JacobiSVD<MatrixXd> svd(A, ComputeFullU | ComputeFullV);
    Matrix<double, 4, 1> x = svd.matrixV().col(3);
    Quaterniond estimated_R(x);
    ric = estimated_R.toRotationMatrix().inverse();//所求的x是q^b_c，在最后需要转换成旋转矩阵并求逆。
    //cout << svd.singularValues().transpose() << endl;
    //cout << ric << endl;
    Vector3d ric_cov;
    ric_cov = svd.singularValues().tail<3>();

    //至少迭代计算了WINDOW_SIZE次，且R的奇异值大于0.25才认为标定成功
    if (frame_count >= WINDOW_SIZE && ric_cov(1) > 0.25)
    {
        calib_ric_result = ric;
        return true;
    }
    else
        return false;
}

从零开始学习三维视觉核心技术SLAM，扫描查看介绍，3天内无条件退款

欢迎关注公众号：计算机视觉life，一起探索计算机视觉新世界~ 早就是优势，学习切忌单打独斗，这里有教程资料、练习作业、答疑解惑等，优质学习圈帮你少走弯路，快速入门！

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、检测分割识别、三维视觉、医学影像、GAN、自动驾驶、计算摄影、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~