平坦的宇宙,寒冷的未来
有很多希望,无限多的希望——但不是我们的。
——卡夫卡
人类花了很长的时间才搞清楚地球是圆的这件事。然而这并不奇怪,因为人类实在太渺小,在地球上来回走动的我们很难察觉到地球的曲率。对于我们而言,自然会以为地球在所有方向上都是平坦无垠的。
当涉及到宇宙的形状时,我们很容易犯类似的错误。对我们来说,它似乎就是无限、且无弯曲的。但这未必是唯一的可能性。
根据爱因斯坦的广义相对论,我们知道大质量的天体能弯曲周围的时空。基于这个理论和一些其他假设,宇宙学家们已经研究出了三种宇宙的可能形状,不同的形状取决于宇宙包含了多少物质。
○ 宇宙是闭合的?开放的?还是平坦的?。| 图片来源:Symmetry Magazine
第一种可能性是宇宙中的物质密度(单位体积内物质的平均数量)是非常高,使得宇宙绕着这些物质弯曲,形成一个类似三维球体形状的空间。我们很难去直观的想象这样一个3D球体空间,但能较容易的在数学上对其进行描述,并具有正的曲率值。如果宇宙的曲率为正,那么它就是有限的,像一个球体的表面一样。更重要的是,除非宇宙中真的存有大量被称为暗能量的神秘物质,否则所有质量所能产生的引力将最终阻止宇宙继续膨胀、导致其不断地收缩。最终,宇宙将在一场大坍缩(Big Crunch)中终结。
○ 球体的表面是有限、但没有边缘的。一个在球面上的三角形的内角和大于180度。如果宇宙的曲率为正,那么它的几何形状就是一个三维球体空间。| 图片来源:PlusMagazine
那么如何判断宇宙的曲率呢?我们可以通过——绘制三角形——来验证一个给定的空间是否是正面弯曲的。我们知道,如果要在球面上的两个点之间沿最短路线行进,那么应该沿着这两点和球心所组成的大圆运动。如果绘制的三角形的边长是由大圆片段组成的,那么有别于二维平面空间的是,它的内角之和会超过180度。
○ 马鞍面。在马鞍面上绘制的三角形的内角加起来小于180度。如果宇宙的曲率为负,那么它的几何形状就是一个无限延伸的马鞍形三维空间。| 图片来源:PlusMagazine
另一种可能性是物质的密度太低,导致宇宙的曲率是负值。在这种情况下,宇宙像是一个三维的马鞍。这样的情况下,三角形的内角和加起来会小于180度,宇宙则趋近于无穷大。要可视化这样一个三维的双曲空间非常困难,但是同样幸运的是,我们用数学就能轻松地对它进行描述。这种情况下,由于没有足够的物质来显著减缓宇宙膨胀的速度,导致宇宙终将迎来寒冷而孤独的大冻结(Big Freeze)。
○ 一个平直的平面。在这个平面上绘制的三角形的角度加起来恰好为180度。如果宇宙的曲率为零,那么它的几何形状就是我们所熟知的普通三维空间。| 图片来源:PlusMagazine
最后第三种可能,就是宇宙的曲率为零——三角形的内角和恰好为180度,宇宙趋近于无穷大。如果是这种情况的话,那么物质或许可以一定程度上减缓宇宙的膨胀速率,但永远不可能将其降至为零。因此,宇宙也同样会终结于大冻结中。
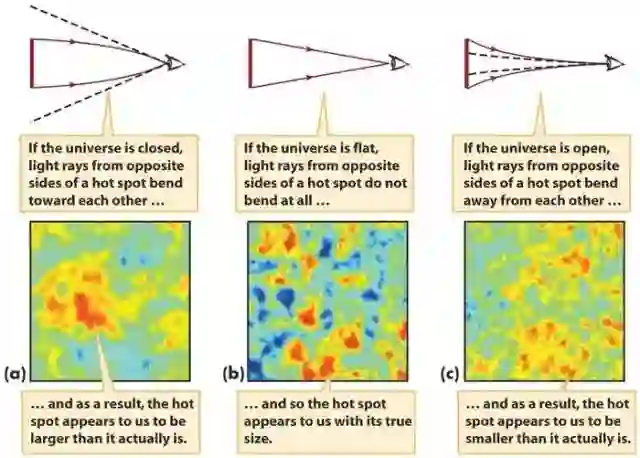
用肉眼观望我们的天空并不能告诉我们宇宙的形状究竟是这三种可能性中的哪一种。幸运的是,宇宙本身提供了一个很好的方法来测量空间曲率:宇宙微波背景辐射的扰动——不同的空间曲率对它造成不同程度的影响。换句话说,空间的几何特征会反映在宇宙微波背景辐射上。
○ 左:假如宇宙是闭合的,在宇宙微波背景中的“热点”会比理论预测的值更大;中:假如宇宙是平直的,这些“热点”看起来就会不大也不小;右:在开放宇宙中,“热点”看上去会比理论值小。| 图片来源: Smoot group at Lawrence Berkeley Labs
通过对微波背景辐射的测量,我们可以得出一个结论:宇宙是平坦的。普朗克卫星与SDSS的最新联合数据告诉我们,如果宇宙是弯曲的——不管是正曲率或负曲率——它也是在比可观测宇宙大400倍的范围之外。我们能观测的范围大约是920亿光年。
○ 目前的观测表明,宇宙是平坦的。| 图片来源:Symmetry Magazine
因此,就目前的观测而言,大冻结或许就是宇宙的终极命运吧。
撰文:Marianne Freiberger
编译:不二北斗
原文链接:https://plus.maths.org/content/shape-and-fate-universe
本文经授权转载自《原理》微信公众号
2018年《物理》杂志开始征订啦!
轻松阅读 享受《物理》

即日起订阅:《物理》 原价240元/年
优惠价:180元/年
微店订阅地址:https://weidian.com/i/2218134089?ifr=itemdetail&wfr=c
扫码咨询
2. 声学超构表面
3. 声学Mie共振及其应用
4. 宇称时间对称性声学
5. 超宽带声螺旋结构
6. 为什么浙江省高考学生选考物理人数大幅下降值得担忧 || 朱邦芬
7. 怀念卓益忠同志
END