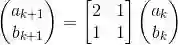一杯咖啡背后的拓扑 | 顾险峰
长岛冬季,时而寒风凛冽,滴水成冰,万木萧疏,天地苍茫;时而斜阳暖照,温润和煦,碧水蓝天,波澜不兴。最近在和朋友们一同探讨拓扑和几何的近现代理论,赏心悦目,踏雪寻梅。恰逢下周开讲代数拓扑,便以一杯咖啡所引发的复杂物理现象为例,浅谈一下隐藏在这些物理现象背后的拓扑定理。这些耳熟能详的例子非常直观,但是对于这些现象的精确解释却需要现代拓扑知识,最终的证明非常抽象而简短,凝炼如诗。
假如我们柔顺舒缓地搅拌咖啡,避免产生气泡,然后抽离咖啡勺,咖啡会自行旋转,缓慢停止下来。在这一过程中,液体中的每一个分子的位置都会发生移动,移动的方式取决于咖啡杯的形状,咖啡的流体力学性质,搅动的方式等诸多因素,精确分析相对困难。但是我们从拓扑上可以断言:存在一个分子,搅拌过程中离开了初始位置,但是最终它又返回了初始位置。
为了方便讨论问题,我们引入数学符号。令咖啡占据的三维空间区域为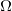
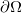
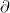
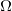
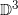
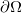
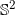
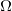
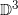
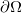
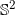
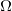
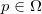
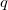
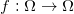

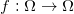
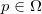

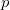
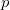
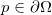
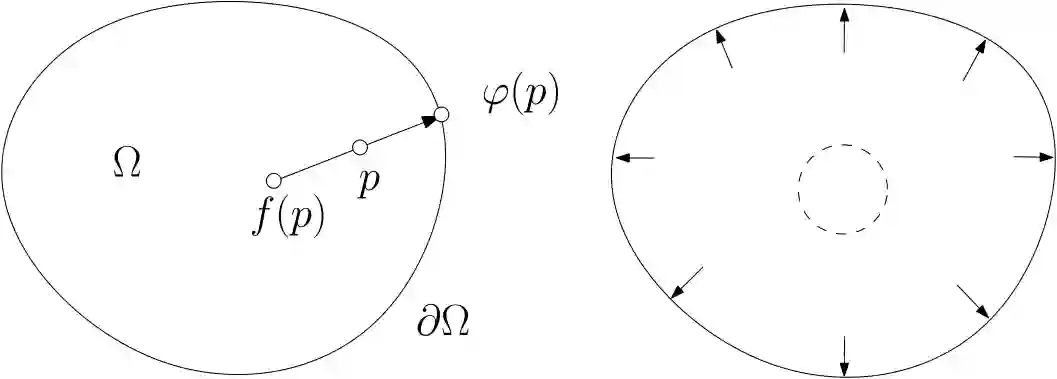
图1. 布劳威尔不动点的证明。
证明的思想非常初等,主要是基于反证法:如图(1)所示,假设不存在不动点,那么对于一切点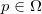
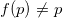
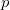
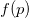
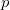
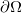
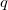


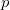
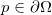

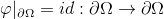
因为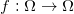

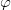

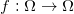
这一证明的关键是压缩映射
对于工程师而言,这一证明足够严格。但是对于数学家而言,物理直觉依赖于人的感官经验,无法达到数学上的严格性要求。问题的关键在于如何将物理直观用数学理论来严格阐述并证明。经过前人艰苦卓绝的探索,人们终于用代数拓扑的方法严格化了这一物理直观。
代数拓扑的基本手法是在拓扑空间上定义各种群,群结构反应了空间的拓扑性质。拓扑空间之间的映射诱导了相应群之间的映射(群同态),这些群的同态反应了拓扑映射的性质。换言之,我们将拓扑范畴映射到代数范畴,并且这个映射保持了结构和关系(即范畴间的映射是函子的)。我们考察拓扑空间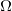
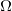
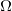
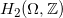
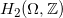
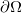
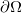
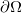
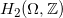
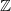

这里第一个箭头表示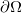
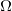
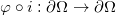
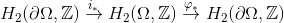
这等价于:

因为中间出现0群,因此复合映射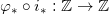
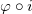
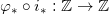

人类通过幼年玩耍建立了物理直觉,那么今天的人工智能算法是否可以胜任呢?首先,我们这里依赖的是降维压缩映射的不存在性,我们无法提供标注训练数据,用人工智能算法学习某种映射的不存在性。其次,代数拓扑层面的代数运算,用吴文俊先生发明的方法原则上能够用符号推理实现出来。但是,计算机只能停留在符号演绎的水平,无法理解群同态序列后面的物理实际。这里至关重要的一步是将物理直觉提炼成概念,形式化成符号体系,总结出代数运算法则。从物理实际抽象成符号体系,这一步人工智能无法完成。这也是人类智能和动物智能的分水岭,更是目前人类智能和人工智能的本质差别之一。
我们进一步观察咖啡拉花的模式。咖啡表面被分割成白色的牛奶泡沫区域和褐色的咖啡脂泡沫区域,奶泡区域作为前景,咖啡泡区域作为背景,构成各种图案。我们缓慢搅拌咖啡,拉花的模式将会变得愈发复杂,最后和背景充分融合。我们试图理解拉花模式的变化规律,和融合速率的定量描述。
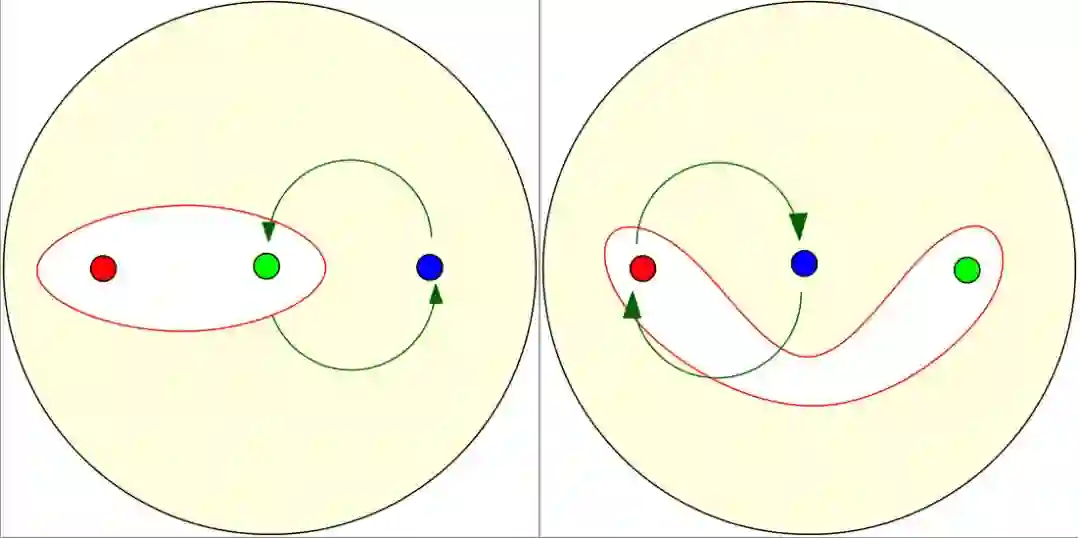
图2. 搅拌咖啡诱发拉花模式的变化。(两次旋转算作一次迭代映射。)
图(2)显示了一个搅拌过程的理想实验,白色区域代表牛奶泡沫,淡黄色区域代表咖啡脂泡沫。我们放置3个用于搅拌的咖啡勺,用红绿蓝三个圆洞代表。每一次搅拌固定一个咖啡勺,另外两个咖啡勺旋转互换,如图中深绿色圆弧所示。白色区域将会被拉长折叠,拉花模式趋于复杂。几次迭代之后,白色区域的边界曲线就很难徒手画出来。
图3. 太妃糖拉伸器。(Taffy Puller)
如果缺乏日常生活经验的话,这里的描述可能依然费解。在曼哈顿有几家中餐馆,大厨在临街的玻璃橱窗中做手工抻面或者各种面点,手工拉面的过程和这个搅拌过程比较相像,面条被多次拉伸和折叠,愈来愈细。在很多美国糖果店都有一种太妃糖销售,太妃糖和中国的麦芽糖相近,非常粘稠,延展性较强。糖果店中经常有一种太妃糖拉伸器(Taffy Puller),由多根不锈钢圆柱构成。太妃糖做成的圆环套在两根圆柱上,这些圆柱在空中依照固定模式旋转,太妃糖被拉伸折叠,自我缠绕,变得愈来愈细,材质混合均匀。
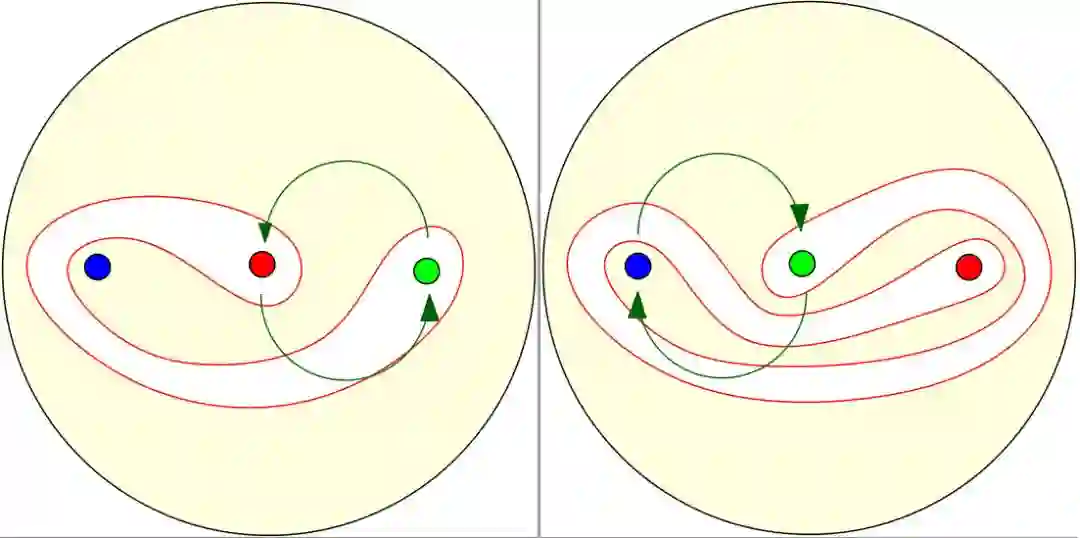
图4 搅拌的动态示意图。
图(4)显示了最为简单的太妃糖拉伸器的动态搅拌过程,非常像模式复杂的抻面过程。很多时候,小孩在糖果店目不转睛地看着太妃糖拉伸器在运转,旁边的父母经常不耐烦地催促。实际上小朋友在努力地学习拓扑。可能当年的瑟斯顿(Thurston)就是这样一个小孩。依随搅拌次数的增加,太妃糖的曲线演化得愈发复杂,但是瑟斯顿天才地发现了某种不变的模式。
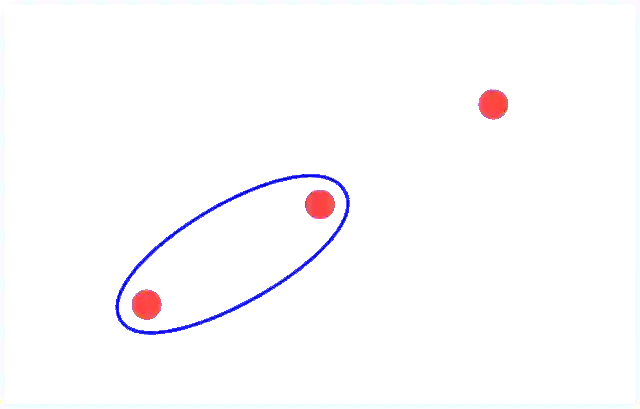
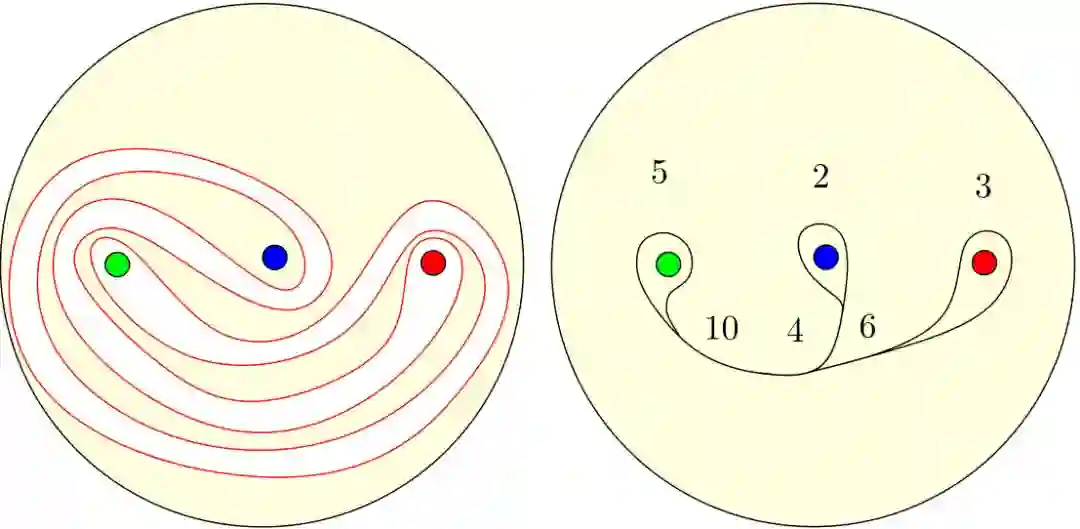
图5. 拉花变换中的不变量:火车道(train track)。
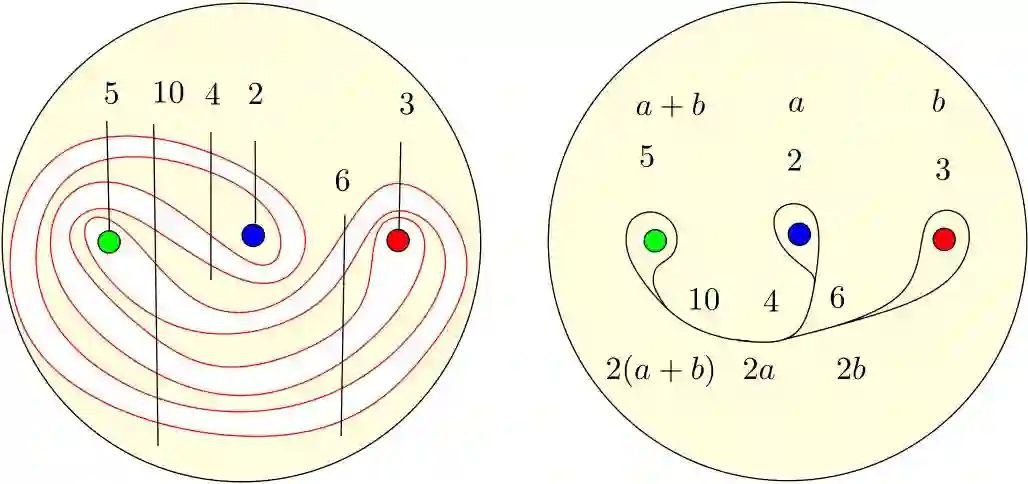
图6. 拉花变换中的不变量:第二次迭代映射后的火车道权重(train track weight)。
我们将咖啡表面视作圆盘上去掉三个点,每次搅拌看成一次自映射,封闭曲线在自映射的迭代下变成另外一条曲线。如图(5)所示,我们在咖啡表面上将彼此平行的曲线段捏在一起,得到一个分支(branch),分支的权重等于多少股被捏成这条分支。分支在道岔(switch)处汇合,两条驶入分支汇聚成一条驶出分支,驶入分支的权重之和等于驶出分支的权重。图(6)左帧的每条竖线代表一条分支(branch),竖线和曲线的交点个数等于这一分支的权重。这样我们得到了所谓的火车道(train track)模型。这个火车道实际上只有两个独立变量a和b,其他权重都可以由(a,b)推出。
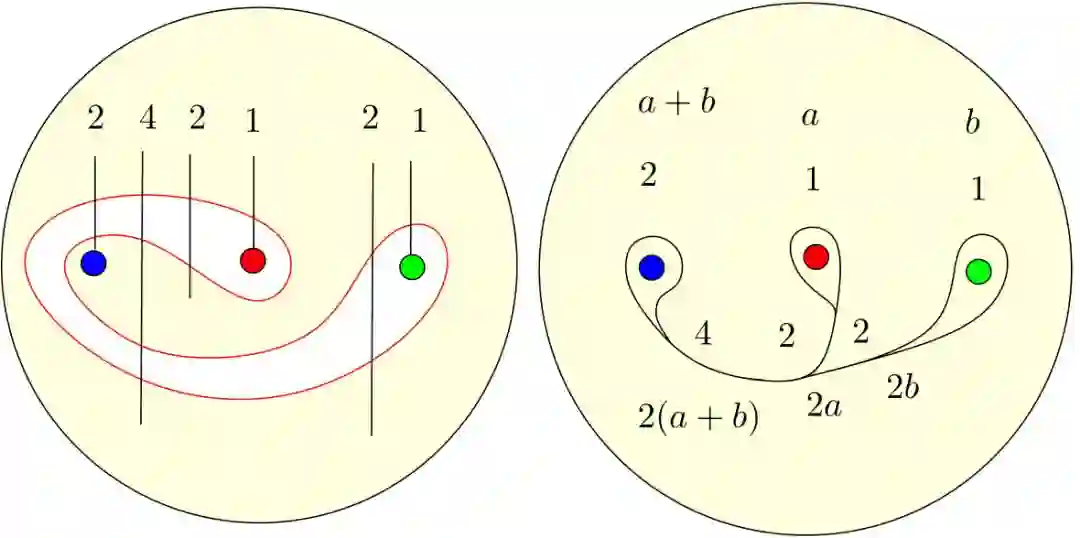
图7. 第一次迭代后的火车道权重。
每条封闭曲线都可以被一个火车道来代表。同时,每个火车道可以表示无穷多条闭曲线。对比图(2)的左下帧和图(5)的左帧,我们看到经过迭代后,曲线发生了巨大变化,但是它们对应的火车道却是相同的。这意味着在这种搅拌方式下,迭代的拉花愈来愈复杂,但是它们对应的“火车道”却是不变的。迭代过程中,火车道分支上的权重满足线性映射:
进一步观察,我们发现在迭代中火车道的权重满足斐波那契数列,因此曲线的长度和迭代次数满足指数关系,n次迭代后曲线长度的n次方根收敛到一个常数,被称为是搅拌映射的拉伸系数。这个拉伸系数等于上述矩阵的特征根,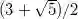
瑟斯顿将这一观察进行了深刻的推广,建立了曲面映射分类的宏伟理论,其核心思想依然是布劳威尔不动点定理。给定一个拓扑曲面,假设其欧拉示性数为负。曲面上所有的简单闭曲线都可以用火车道来表示。曲面也可以配备双曲黎曼度量,即高斯曲率处处为-1的黎曼度量。依据Teichmuller理论,所有的双曲度量构成一个高维空间的球体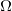
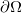
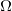
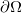
瑟斯顿的理论抽象而深刻,但是观察咖啡拉花,我们可以体会其内在精髓。平易近人的布劳威尔定理给出了严格的证明,但是这里紧化Teichmuller空间的理解需要较深的数学涵养和天马行空的想像力。
从应用层面上来讲,所有的方程求解问题等价于求不动点问题,代数方程、微分方程和积分方程都可以统一到这个框架之下。所有的迭代算法问题也可以归结为求解不动点问题,动漫动画的图像渲染等价于求解一个积分方程的不动点,人工智能中的对抗生成网络(GAN)等价于求解纳什均衡点。这些方程解的存在性和算法的收敛性都是基于布劳威尔不动点定理的某种形式的推广。
品咖啡是很多人日常生活的一部分。从一杯咖啡的搅拌我们可以想象到布劳威尔不动点,从奶泡拉花我们可以观察到曲面自映射的动力学,其背后隐藏的拓扑学原理抽象而凝炼,却又质朴而直观,从中我们可以体会到拓扑学的简洁优美和人类抽象思维的深邃精密。
本文经授权转载自《老顾谈几何》微信公众号
2018年第一期已经出版,欢迎订阅全年杂志!
轻松阅读 享受《物理》

即日起订阅:《物理》 原价240元/年
优惠价:180元/年
微店订阅地址:https://weidian.com/i/2218134089?ifr=itemdetail&wfr=c
扫码咨询
3. 打开生命时钟,重塑生命节律 ||2017年诺贝尔奖专题
4. 冷冻电镜:在原子尺度上观察生命 || 2017年诺贝尔奖专题
5. 时空与物质、广义相对论与量子力学的完美结合——深度科普解读双中子星并合多信使观测
6. 从2017诺贝尔物理学奖展望新加坡未来科学的发展方向 || 2017年诺贝尔奖专题
7. 为什么浙江省高考学生选考物理人数大幅下降值得担忧 || 朱邦芬
END