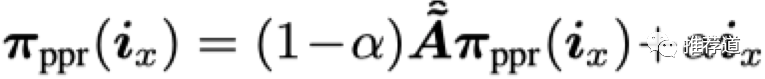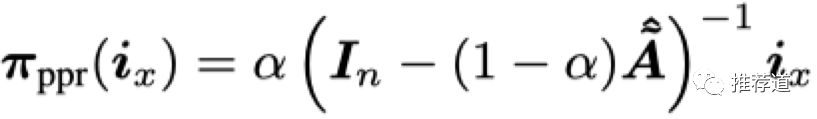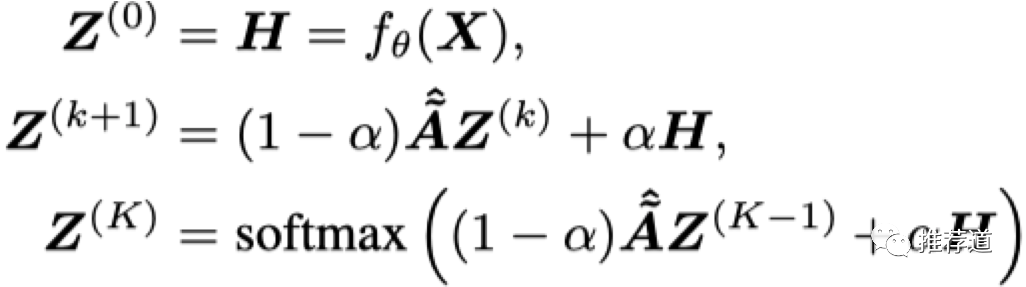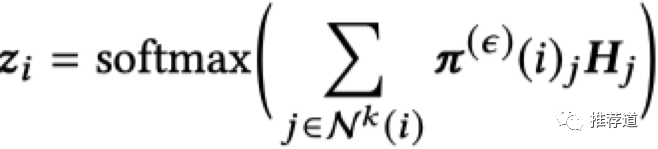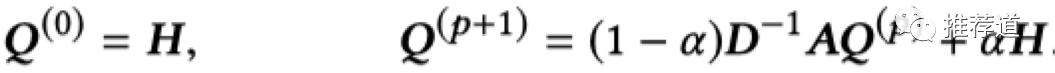Google PPRGo: 两分钟分类千万节点的最快GNN

今天给大家介绍的论文是《Scaling Graph Neural Networks with Approximate PageRank》(TensorFlow源码)。这篇论文由Google Research和Technical University of Munich共同发表于KDD 2020。文中提出了PPRGo模型用于图上的节点分类，其最引人注目的特点就是一个“快”字。根据论文中的实验结果，在一个包含1240万个节点，17300万条边组成的大规模图上，PPRGo只花了不到2分钟就给图上所有节点分了类，更夸张的是，这2分钟还是包括了预处理、训练、预测的全流程时间。

面对性能如此强悍的GNN后起之秀，各位勤奋好学的炼丹师、调参侠、打工人，是不是都迫不及待地想一探PPRGo的庐山真面目？那好，本文将带领各位看官，追溯PPRGo模型的前世今生，探究它“神速”背后的奥秘，也扒一扒它的"阿喀琉斯脚踝"在哪里。

传统GNN的痛点

为了搞清楚PPRGo为什么能够这么快，首先我们要搞清楚以往的GNN模型为什么那么慢？

一个传统的两层GCN如下所示，

• 其中 和 分别是第1和第2层卷积待优化的参数，
• ,
• 最后加一个softmax用于节点分类。

因为只用了2层卷积，所以只利用了 目标节点两跳之内的邻居信息。

为了提高模型的性能，需要利用目标节点更多、更远的邻居信息。传统GCN要达到这个目的，只能通过增加卷积的层数。但是，增加卷积层数是把双刃剑，在扩大模型的receptive field的同时，也面临着如下的困难。

卷积层数多了，容易over smoothing

所谓的over smoothing现象，是指经过多层卷积之后，图上每个节点的embedding收敛于相同或相似的向量，变得难以区分。为什么会出现over smoothing的现象，论文《Representation Learning on Graphs with Jumping Knowledge Networks》给出了一种解释：

• 图卷积与PageRank的计算原理是相通的，都是节点自身的信息（PageRank是节点的影响力）沿边向邻居传递，并与邻居的信息(PageRank中是节点影响力)融合
• PageRank中的这个信息传递过程最终会收敛，收敛时各节点的PageRank得分，就是该节点在图中的全局影响力
• 当卷积层数增加时，每个节点对其他节点的影响力也将收敛于该节点的PageRank。 这个影响力是全局唯一的，不会因target node不同而变化，导致各节点在信息融合之后的embedding也会趋同。

所以，更合理的做法时，当为target node聚合周围邻居的信息时，应该多考虑那些对target node更重要的节点，即针对target node的Personal PageRank（PPR）更高的节点，而不是全局影响力(PageRank)更高的节点。举个例子，在全球所有人组成的网络中，美国总统的影响力（PageRank, PR）肯定比我的老板要高，但为什么我敢骂川普，却不敢骂我的老板? 因为我的老板针对我的Personal PageRank (PPR)比川普高多了😂。

卷积层数多了，增加了要学习的参数

图卷积中信息的transformation与propagation都是由各层卷积完成的，所以每层都有待优化的参数（比如上图中的 和 ）和激活函数，来完成信息的transformation。增加卷积层数，就意味着引入更多的参数要学习，既增加了学习的难度，也容易让模型overfitting。

卷积层数多了，增加了计算耗时

随着卷积层数的增加，计算目标节点所需要的邻居节点数也指数级增加，与之相关的CPU、内存压力也随之增加。即使采取了neighbor sampling，也未能改变这种指数级增加的趋势。关键是每个batch都必须重复承受这种计算压力，而无法amortize。

正因为基于逐层卷积的GNN有以上这么多的缺点，本文的作者在ICLR 2019发表论文《PREDICT THEN PROPAGATE : GRAPH NEURAL NETWORKS MEET PERSONALIZED PAGERANK》，提出用PPR取代逐层卷积，来完成节点信息在图上的传播与融合。那篇论文提出的PPNP（Personalized propagation of neural predictions）模型也就是是PPRGo模型的前身。在学习PPNP模型之前，先让我们花点时间重温一下PageRank和Personal PageRank。

重温PageRank和Personal PageRank

PageRank的原理，照抄wikipedia。注意，PageRank是各节点在整个图上的全局影响力，与从哪个节点开始surfing无关。

图中高亮的部分就是Personal PageRank（PPR）与PageRank（PR）的不同之处：当用户不再点击外链时，不再随机浏览其他网页，而是跳回（teleport）到最开始出发的网页，重新开始surfing。这种情况下，计算出来的各节点的影响力，就是针对起始节点的PPR。

PR/PPR的公式经过反复迭代，会趋于收敛，收敛时满足：

• 是一个One-Hot Encoding，只有起始位置x上才有1，其他位置都是0
• , ，是考虑了self-loop的对称归一化后的邻接矩阵
• 是wikipedia公式中的1-d，表示teleport的概率，控制选择邻居的范围。 接近1，说明更注重immediate neighbor； 接近0，说明更注重multi-hop neighbors。

解这个方程，得到 ，其中的第y位表示节点x对节点的y的影响力。

要计算所有节点对其他所有节点的PPR，就把 换成单位矩阵 ，得到 。其中的[y,x]位置上的元素，代表节点x对节点y的影响力，因为存在对称性，也代表y对x的影响力。

求解 的意义在于：

• PR/PPR的思想，都来源于surfing或者说random walk。经过无数轮的surfing或游走，各节点的分数收敛于各自的PR或PPR。这是一种类似Monte Carl的 仿真求解方式。
• 而 提供了一个“ 解析解”， 效果等同于经过无穷轮surfing之后收敛的效果，但是省却了那无穷轮surfing的过程。

PPNP：基于PPR完成信息在图上的传递

正如上一节所述，假如我们能够计算出 矩阵，即图中任意节点对其他节点的影响力，我们可以借助 将每个节点的本地信息传播到图上的任意节点。其效果等同于经过无穷层卷积的效果，却省去了逐层卷积的麻烦。

基于PPR的GNN非常简单，只需要两步：

1. 只拿每个节点的 本地特征，喂入本地模型 ，得到每个节点的本地向量表示，
2. 如果已知 矩阵，则 目标节点的最终向量表示=sum(邻居节点的本地向量 * 邻居对target node的PPR)。再喂入softmax，就得到每个节点对每个类别的概率

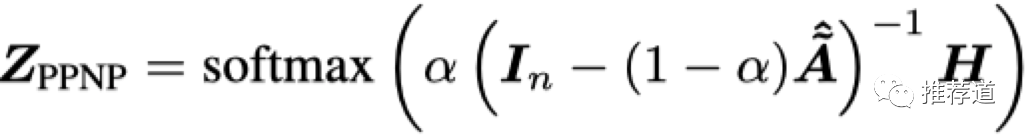
Power Iteration近似求解

但问题是，求解 的过程中需要求逆，一来大型矩阵求逆本来就困难，二来求逆破坏了矩阵的稀疏性，增加了计算复杂度。

所以PPNP利用“PPR本来就是多轮迭代收敛后的产物”的思路，用power iteration代替 ，而且迭代过程中只涉及稀疏矩阵运算，也降低了计算复杂度。

特点与优势

• 在这个模型中， 节点信息的transformation与propagation彻底分离：
• transformation只由本地模型 完成，可以容纳复杂模型
• propagation由 完成，其中没有需要优化的参数
• 尽管也采用了power iteration，但是其近似的是PPR的解析解， 其理论效果等同于使用了无穷层卷积，等同于聚合了图上所有节点的信息，但是却节省了那无穷层卷积的耗时与训练参数
• 计算PPR时，引入teleport，使PPR相对于逐层卷积收敛到的PR， 对目标节点的针对性更强，避免了多层卷积带来的over smoothing。

PPRGo：PPNP的升级版本

PPRGo与PPNP师出同门，所以基本思路是一致的，都是先用每个节点的本地特征学习出每个节点的本地embedding，再用PPR矩阵完成本地embedding在图上的传递与聚合。但是与PPNP不同的是：

• PPNP由于求逆困难，实际上没有真正求解出 ，而是采用Power Iteration代替 。这种方式的缺点，一是计算 需要经过多次迭代（原文中需要10次以上），二是每个batch都要拿当前batch中的H重新迭代计算
• PPRGo找到了近似求解 的算法。 我们只需要在训练前将 提前计算好，训练每个batch时无需重新计算，从而大大加快了训练速度。

提前计算好PPR矩阵

PPRGo采用《Local graph partitioning using pagerank vectors》中的算法来近似求解PPR矩阵。针对目标节点"t"，计算其他节点对"t"的PPR的算法如下所示。具体算法推导，请感兴趣的同学移步原论文，这里就不展开了。

对于训练集中的每个节点，我们都需要运行以上算法，计算其他节点对其的PPR。针对不同目标节点的计算流程，相互独立，非常便于分布式计算。

训练

知道了其他节点对目标节点的影响力（PPR），则目标节点的最终embedding=sum(邻居节点的本地embedding * 邻居对target node的PPR)。

为了进一步加速训练，PPRGo决定利用稀疏化进一步减少计算次数，即目标节点的embedding，是针对目标节点影响力最大的k个邻居的本地embedding的加权和。这种思路源自对实际网络的观察，能够针对某节点发挥作用的节点毕竟是少数，大多数其他节点针对目标节点的PPR都是非常小的数，不如将它们强制置为0，免得浪费算力。

因此，每个目标节点最终的分类概率如下所示

• 是其他节点针对目标节点"i"的PPR组成的向量
• 是 中数值最大的Top-K个元素的下标，代表着对节点“i”影响力最大的k个节点
• 是节点"j"的本地embedding
• 一般来说，节点"i"对自身的影响力是最大的，因此 通常也考虑了节点i的本地embedding

接下来的训练过程就非常常规了，无须就是最大熵损失函数+SGD那一套。

预测

在semi-supervised node classification问题中，面对一个含有n个节点的图，往往只有少数节点有label，还有m(占n的绝大多数)个节点的label待预测。

本来，我们可以遵循与训练时一样的做法，即

• 是m*n的矩阵，表示所有节点针对待预测节点的影响力
• H是所有n个节点的本地向量表示

这种作法的缺点在于，第一步计算m个节点的PPR矩阵，当m非常大的时候，就要耗费不少时间。关键是，计算出来的 只用一次，而不像训练时那样被每个batch反复使用。因此，有点得不偿失。

为此，PPRGo在预测时，又切换回使用power iteration的方法。根据论文中的实验，只需要2~3次迭代，就可以获得较高精度，而且 是稀疏矩阵，方便计算。

总结

优点

至此，关于PPRGo的前世今生，就介绍完毕，总结一下它的优点。

• 传统“多层卷积”GNN面临两难选择：
• 要想提高精度，需要聚合更多邻居，就需要更多层卷积；
• 但是增加层数，会导致over smoothing，而且增加了学习参数和训练时间。
• PPRGo 用PPR矩阵代替“多层卷积”完成节点信息在图上的传递与聚合，相当于用“解析方式得到的近似解”代替“多轮游走的仿真解”，从而带来如下优点：
• PPR通过引入teleport，能够找到针对目标节点影响力最大的节点，而不是全局影响力最大的节点，从而避免over smoothing。
• 节点信息的transformation与propagation相离，不会为了要融合更多邻居而引入更多的优化参数。
• PPR理论上等效于无穷层卷积的结果，却省去了无穷层卷积的麻烦。拿节点本地embedding，通过一次稀疏矩阵乘法，就相当于无穷层卷积，相当于聚合了图上所有节点的信息，大大提升了运算速度。

限制

尽管有以上优点，但是PPRGo还没有强大到代替多层卷积的图神经网络的地步，主要是其应用范围还比较窄

• PR/PPR，不适用于异构图，甚至不能用于二部图。在推荐系统常见的user-item二部图中，user对item的影响力，user对其他user的影响力，根本不在一个衡量体系下，也就无法统一用一个数字来表示。
• PPNP与PPRGo本质上都是 拿PPR对本地embedding进行加权求和。这种线性加权聚合的方式比较简单，像GraphTR所使用的FM、Transformer这些复杂的信息聚合方式，是无法实现的。
• 个人感觉 只能用于node classification。像推荐系统比较关心的link  prediction问题，需要在信息聚合时忽略待预测的边，否则会造成信息泄漏，而PPRGo“神速”的法宝就是 提前计算好PPR矩阵，肯定是不支持这种“动态忽略边”的操作的。

---

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方"AINLP"，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

欢迎加入图神经网络交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注图神经网络

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。

阅读至此了，分享、点赞、在看三选一吧🙏