神经网络中的常用激活函数总结
©PaperWeekly 原创 · 作者|张文翔
单位|京东集团算法工程师
研究方向|推荐算法

[1] 如果在前向传播的过程中使用了不可导的函数,是不是就不能进行反向传播了?
https://www.zhihu.com/question/297337220/answer/936415957
[2] 为什么神经网络中的激活函数大部分都是单调的?
https://www.zhihu.com/question/66747114/answer/372830123
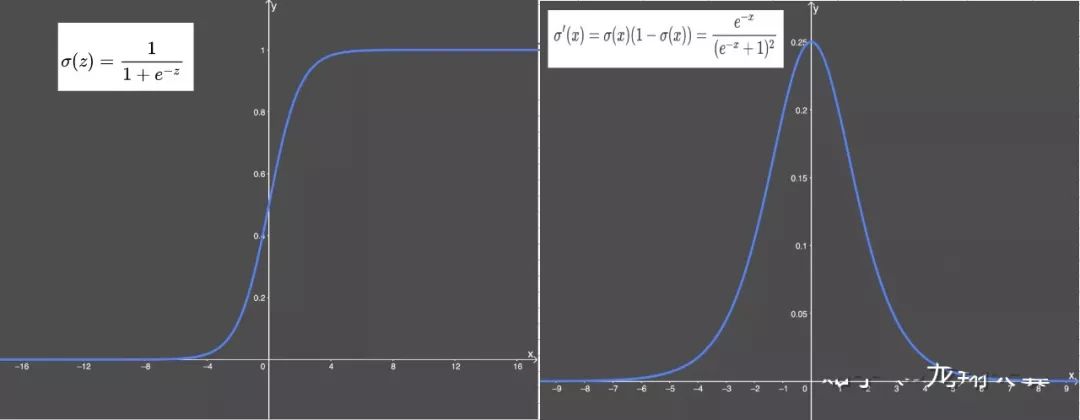
梯度平滑
输出值在 0-1 之间
激活函数计算量大(在正向传播和反向传播中都包含幂运算和除法);
梯度消失:输入值较大或较小(图像两侧)时,sigmoid 函数值接近于零。sigmoid 导数则接近于零,导致最终的梯度接近于零,无法实现更新参数的目的;
Sigmoid 的输出不是 0 为中心(zero-centered)。
梯度平滑
输出值在 0-1 之间
激活函数计算量大(在正向传播和反向传播中都包含幂运算和除法);
梯度消失:输入值较大或较小(图像两侧)时,sigmoid 函数值接近于零。sigmoid 导数则接近于零,导致最终的梯度接近于零,无法实现更新参数的目的;
Sigmoid 的输出不是 0 为中心(zero-centered)。
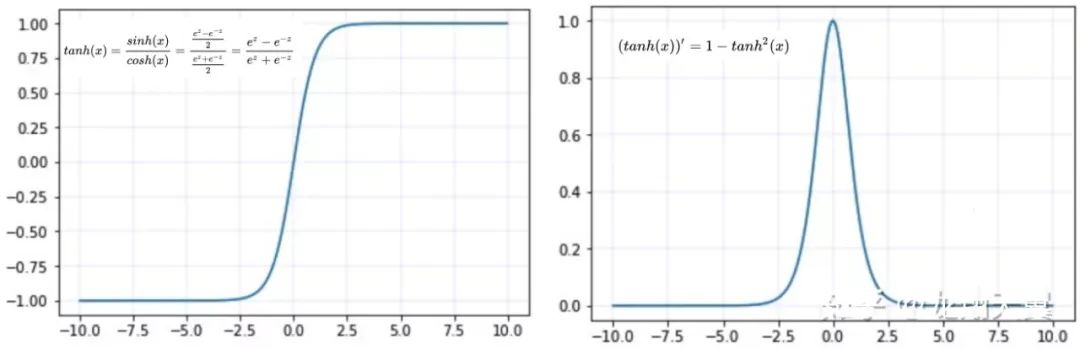
同 sigmoid
tanh(x) 的梯度消失问题比 sigmoid 要轻,收敛更快
输出是以 0 为中心 zero-centered
缺点:
同 sigmoid
简单高效:不涉及指数等运算;
一定程度缓解梯度消失问题:因为导数为 1,不会像 sigmoid 那样由于导数较小,而导致连乘得到的梯度逐渐消失。
缺点:
dying Relu:即网络的部分分量都永远不会更新,可以参考:
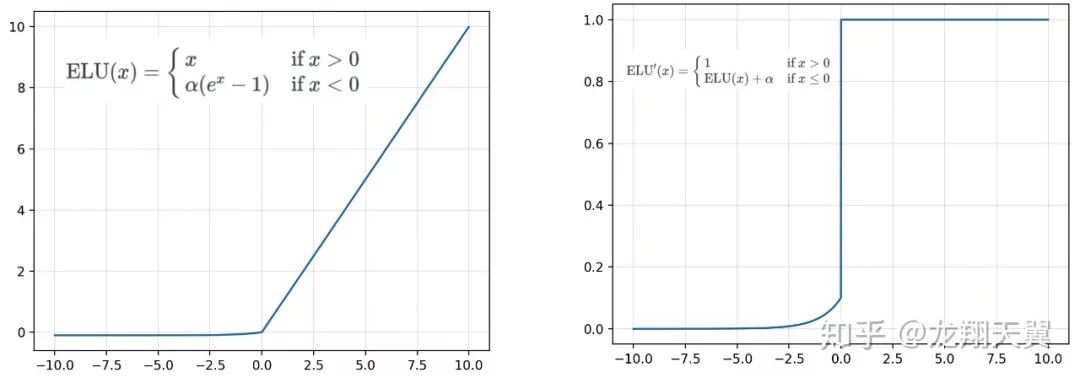
4. 指数线性单元(ELU)
能避免死亡 ReLU 问题:x 小于 0 时函数值不再是 0,因此可以避免 dying relu 问题;
能得到负值输出,这能帮助网络向正确的方向推动权重和偏置变化。
缺点:
计算耗时:包含指数运算;
α 值是超参数,需要人工设定
5. 扩展型指数线性单元激活函数(SELU)
lambda = 1.0507
alpha = 1.67326
SELU 激活能够对神经网络进行自归一化(self-normalizing);
不可能出现梯度消失或爆炸问题,论文附录的定理 2 和 3 提供了证明。
缺点:
应用较少,需要更多验证;
lecun_normal 和 Alpha Dropout:需要 lecun_normal 进行权重初始化;如果 dropout,则必须用 Alpha Dropout 的特殊版本。
6. 渗漏型整流线性单元激活函数(Leaky ReLU)
类似于 ELU,能避免死亡 ReLU 问题:x 小于 0 时候,导数是一个小的数值,而不是 0;
与 ELU 类似,能得到负值输出;
计算快速:不包含指数运算。
缺点:
同 ELU,α 值是超参数,需要人工设定;
在微分时,两部分都是线性的;而 ELU 的一部分是线性的,一部分是非线性的。
7. Parametric ReLU (PRELU)
alpha=0:退化为 ReLU
alpha 固定不更新,退化为 Leak_ReLU
与 ReLU 相同。
缺点:
在不同问题中,表现不一。
8. 高斯误差线性单元(Gaussian Error Linear Unit,GELU)
随着 x 的降低,它被归零的概率会升高。对于 ReLU 来说,这个界限就是 0,输入少于零就会被归零;
与 RELU 类似:对输入的依赖;
与 RELU 不同:软依赖 P(X≤x),而非简单 0-1 依赖;
直观理解:可以按当前输入 x 在其它所有输入中的位置来缩放 x。
在 NLP 领域效果最佳;尤其在 Transformer 模型中表现最好;
类似 RELU 能避免梯度消失问题。
缺点:
2016 年提出较新颖;
计算量大:类似 ELU,涉及到指数运算。
9. Swish by Google 2017
β 是个常数或可训练的参数,通常所说的 Swish 是指 β=1;
β=1.702 时,可以看作是 GELU 激活函数。
据论文介绍,Swish 效果优于 ReLU:
https://arxiv.org/abs/1710.05941v2
计算量大:sigmoid 涉及到指数运算。
10. Mish by Diganta Misra 2019
根据论文介绍:
https://arxiv.org/abs/1908.08681
Mish 函数保证在曲线上几乎所有点上的平滑度;
随着层深的增加,ReLU 精度迅速下降,其次是 Swish。而 Mish 能更好地保持准确性。
2019 年提出,需要时间和更多实际应用验证。
11. Maxout
Maxout 可以拟合任意的的凸函数
Maxout 与 Dropout 的结合效果比较好
12. Data Adaptive Activation Function (Dice) by alibaba 2018
激活函数的形式相同:f(s) = p(s) * s + (1 − p(s)) · αs
p(s)的计算方式不同:
PReLU:p(s) 是指示函数 I(s>0)
Dice:p(s) 是 sigmoid(BN(s)),BN 代表 Batch Normalization
Dice 可以看作是一种广义的 PReLu,当 E(s) = 0 且 Var(s) = 0 时,Dice 退化为 PReLU。
Dice 受到数据影响,E(s) 决定其 rectified point:PReLU 是在 0 的位置,而 Dice 是在 E(s) 位置。
与Batch Normalization 有异曲同工之妙,可以解决 Internal Covariate Shift 问题。论文 Deep Interest Network for Click-Through Rate Prediction 实验表明 :Dice 效果优于 PReLU。
具体实现可以参考 Dice 代码:
点击以下标题查看更多往期内容:

让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 获取最新论文推荐