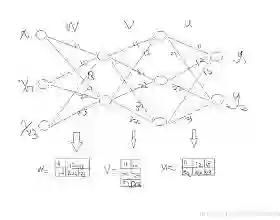
《模型汇总-20》深度学习背后的秘密：初学者指南-深度学习激活函数大全

    激活函数是获取输入信号并将其转换为输出信号。激活函数为网络引入非线性，这就是我们称之为非线性的原因。神经网络是通用函数逼近器，深层神经网络使用反向传播法进行训练，反向传播需要使用可微分的激活函数。Backpropapagation使用此激活函数的下降梯度来更新网络权重。了解激活函数非常重要，因为它们对深层神经网络的函数逼近能力中起着至关重要的作用。在本文中，我列出并描述了常用的激活函数。

· 一致或线性激活函数 

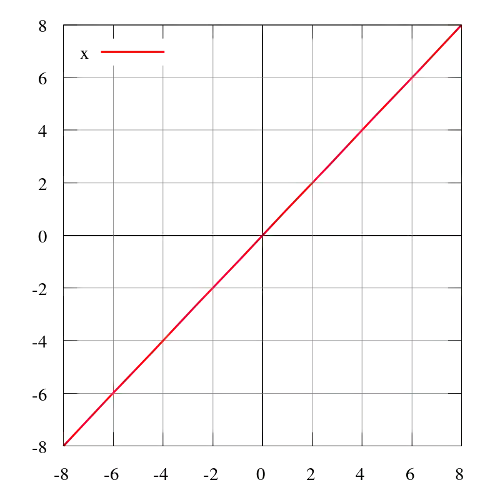
     一致或线性激活函数是最简单的激活函数。它对模型的输入数据应用线性操作，输出数据与输入数据成比例。线性激活函数的问题是它的导数是一个常数，它的梯度也将是一个常数，下降将是一个恒定的梯度。

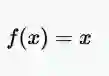
一致或线性激活函数的方程式

范围：（-∞，+∞）

示例：f（2）= 2或f（-4）= -4

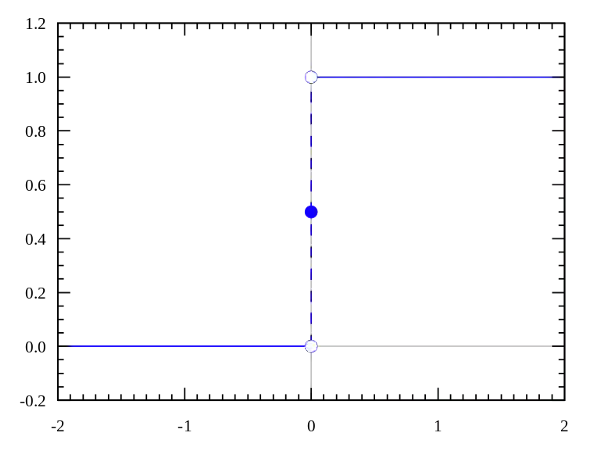
· Heaviside（二值型激活函数，0或1，high或low）步长函数

    通常仅在单层感知器中有用，这是早期类型的神经网络，可在输入数据可线性分离的情况下用于分类。这些函数对二进制分类任务很有用。如果输入累加和高于某一阈值，则输出为A1，如果输入和低于某个阈值，则为A0。感知器使用的值为A1 = 1，A0 = 0

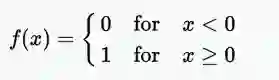
Heaveside /二进制步长函数方程（0或1，高或低）

范围：{0或1} o或1

示例：f（2）= 1，f（-4）= 0，f（0）= 0，f（1）= 1

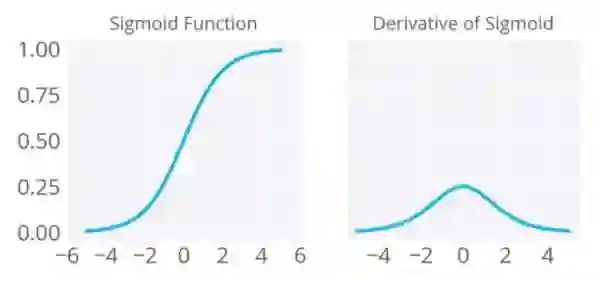
· Sigmoid或Logistic激活函数（Soft Step） -    主要用于二进制分类问题（即输出值范围为0-1）。它有梯度消失的问题。由于输入（X）导致输出（Y）变化非常小，因此网络拒绝学习或某些时期学习非常慢。它是分类问题的广泛使用的激活函数，但最近。这个函数更容易陷入饱和状态，特别是随着网络层次增加，使训练更加困难。计算Sigmoid函数的导数非常简单。

    在神经网络的反向传播过程中，误差信号在每一层（至少）被挤压四分之一。因此，网络越深，数据的更多知识就会“损失”。从输出层得到的一些“大”误差信号可能无法在相对较浅的层中影响神经元的突触权值（“浅”意味着它靠近输入层）

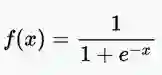
Sigmoid或Logistic激活函数

S型函数的导数

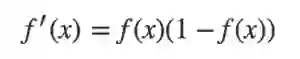
范围：（0，1）

示例：f（4）= 0.982，f（-3）= 0.0474，f（-5）= 0.0067

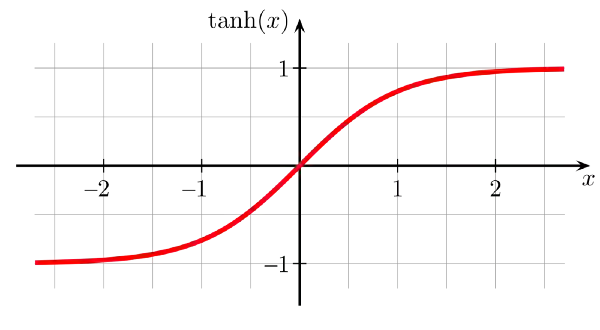
· 双曲正切S型激活函数（TanH） 

    看起来像一个缩放的S形函数。数据以零为中心，因此导数将更高。Tanh比S形和logistic激活函数收敛速度更快。

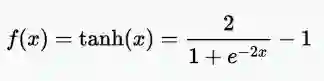
双曲正切（TanH）激活函数方程

范围：（-1，1）

示例：tanh（2）= 0.9640，tanh（-0.567）= -0.5131，tanh（0）= 0

· 正则化线性单元（ReLU） 

    比tanh快6倍。当输入值小于零时，输出值为零。如果输入大于或等于零，则输出等于输入。当输入值为正时，导数为1，因此不会产生类似S形激活函数在误差反向传播时出现的挤压效应（Squeeze effect）。

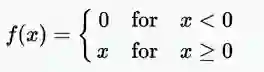
正则化线性单元（ReLU）激活函数的公式

范围：[0，x）

示例：f（-5）= 0，f（0）= 0＆f（5）= 5

    Relu也存在问题，Relu在训练的时候非常脆弱且可能会“死亡”。比如，一个比较大的梯度流经Relu神经元，可能会导致权重以一种方式“die”更新，即神经元对任何的数据都不会被激活。如果这一情况发生，流经这个神经元的梯度对于任意数据永恒为0。也就是说，Relu单元在训练时可能会不可逆的死亡，因此Relu可能会消磨掉数据的多样性。比如，如果学习速率设得过大，你可能发现模型40%的神经元都是死的（比如，神经元对于整个数据集都不会被激活）。对于一个设置合适的学习速率，这个问题就没有那么严重。

· Leaky正则化线性单元（Leaky ReLU）

        Leaky ReLU 在单元未激活时，允许小的非零梯度。0.01是小的非零梯度值。

Leaky正则化线性单元（Leaky ReLU）激活函数的方程

范围：（-∞，+∞）

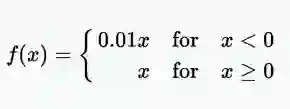
Leaky正则化线性单元（Leaky ReLU）

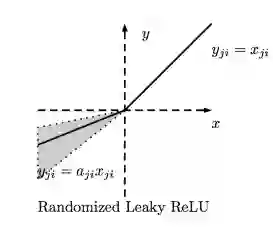
· 参数正则化线性单元（PReLU） - 把Leaky的系数当做一个参数与其他神经网络参数一起学习。Alpha（α）是这里的Leaky系数。

对于α≤1f（x）= max（x，αx）

范围：（-∞，+∞）

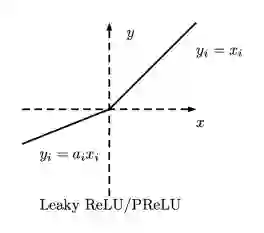
参数正则化线性单位公式（PReLU）

· 随机Leaky正则化线性单元（RReLU）

范围：（-∞，+∞）

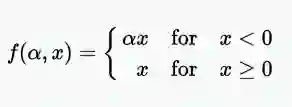
随机Leaky正则化线性单元（RReLU）

· 指数线性单位（ELU） 

    指数线性单位尝试使平均激活更接近于零，从而加快学习。已经表明，ELU可以获得比ReLU更高的分类精度。α是这里的一个超参数并被调整，约束是α≥0（零）。

范围：（-α，+∞）

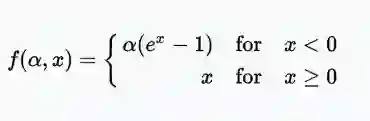
指数线性单位（ELU）

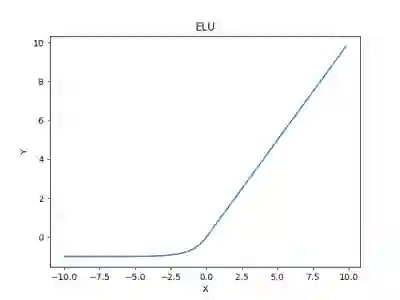
· 缩放指数线性单位（SELU）

范围：（-λα，+∞）

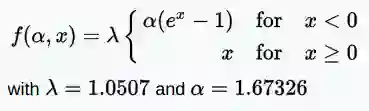
缩放指数线性单位（SELU）

· S形正则化线性激活单元（SReLU）

范围：（-∞，+∞）

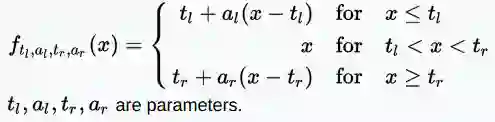
S形正则化线性激活单元

· 自适应分段线性（APL）

范围：（-∞，+∞）

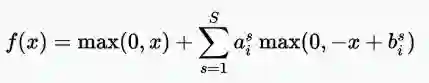
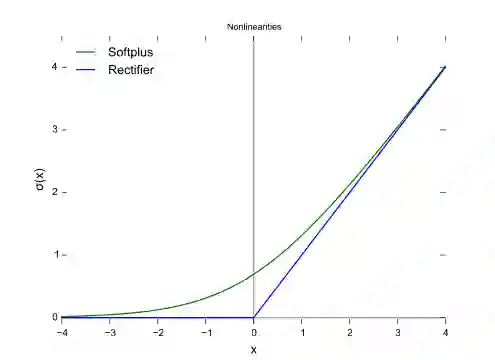
· SoftPlus 

    softplus函数的导数是logistic函数。ReLU和Softplus在很大程度上是相似的，除了接近0（零）时，softplus更加平滑且可微的。计算ReLU值及其导数比softplus函数更容易和高效，因为softplus的公式中包含log（.）和exp（.）计算。

范围：（0，∞）

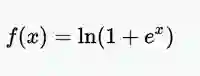
Softplus

softplus函数的导数是逻辑函数。

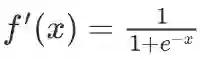
softplus函数的微分

· 弯曲一致激活函数

范围：（-∞，+∞）

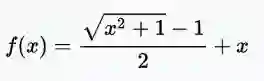
弯曲一致激活函数

· Softmax激活函数

    S个OFTMAX函数将一个粗糙的原始值转换为后验概率。这提供了一定的确定性。它将每个单元的输出压缩在0和1之间，就像S形函数一样。但是它也会将每个输出除以输出的总和，使总的概率等于1。

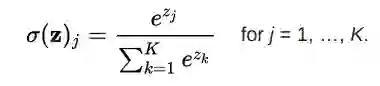
Softmax函数方程

softmax函数的输出等同于分类概率分布，它告诉每个类别的真实概率分布。

结论：

ReLU和它的变体应优于S形或tanh激活函数。同时ReLU训练起来更快。如果ReLU导致神经元死亡，请使用Leaky ReLUs或其他变体。Sigmoid和tanh存在梯度消失的问题，不应该在隐藏层中使用。ReLUs最适用于隐含层。应使用易于微分和易于训练的激活函数。

参考文献：

1. https://en.wikipedia.org/wiki/Activation_function

2. https://github.com/Kulbear/deep-learning-nano-foundation/wiki/ReLU-and-Softmax-Activation-Functions

3. https://en.wikipedia.org/wiki/Rectifier_(neural_networks）

往期精彩内容推荐：

斯坦福大学2017年春季_基于卷积神经网络的视觉识别课程视频教程及ppt分享

ICML17 Seq2Seqtutorial精品资料分享

模型汇总18 强化学习（Reinforcement Learning）基础介绍

模型汇总15 领域适应性Domain Adaptation、One-shot/zero-shot Learning概述

模型汇总-14 多任务学习-Multitask Learning概述

扫描下方二维码可以订阅哦！

DeepLearning_NLP

深度学习与NLP

       商务合作请联系微信号：lqfarmerlq