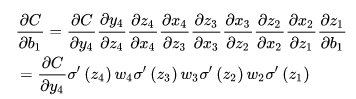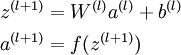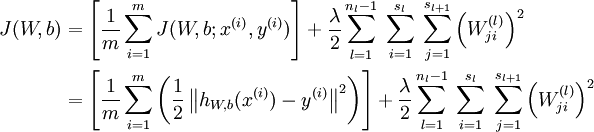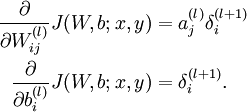BAT题库 | 机器学习面试1000题系列（第131~135题）

上期思考题及参考解析

130.什么是梯度消失和梯度爆炸？

  @寒小阳，反向传播中链式法则带来的连乘，如果有数很小趋于0，结果就会特别小（梯度消失）；如果数都比较大，可能结果会很大（梯度爆炸）。
  @单车，下段来源：https://zhuanlan.zhihu.com/p/25631496
  层数比较多的神经网络模型在训练时也是会出现一些问题的，其中就包括梯度消失问题（gradient vanishing problem）和梯度爆炸问题（gradient exploding problem）。梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。

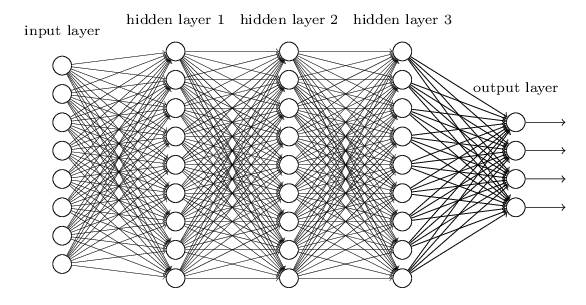
  例如，对于下图所示的含有3个隐藏层的神经网络，梯度消失问题发生时，接近于输出层的hidden layer 3等的权值更新相对正常，但前面的hidden layer 1的权值更新会变得很慢，导致前面的层权值几乎不变，仍接近于初始化的权值，这就导致hidden layer 1相当于只是一个映射层，对所有的输入做了一个同一映射，这是此深层网络的学习就等价于只有后几层的浅层网络的学习了。

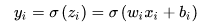
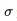
  而这种问题为何会产生呢？以下图的反向传播为例（假设每一层只有一个神经元且对于每一层，其中为sigmoid函数）

  可以推导出

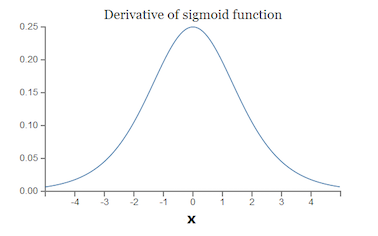
  而sigmoid的导数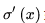如下图

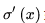
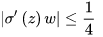
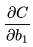
  可见，的最大值为1/4，而我们初始化的网络权值|w|通常都小于1，因此，因此对于上面的链式求导，层数越多，求导结果越小，因而导致梯度消失的情况出现。

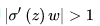
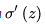
  这样，梯度爆炸问题的出现原因就显而易见了，即，也就是w比较大的情况。但对于使用sigmoid激活函数来说，这种情况比较少。因为的大小也与w有关（z=wx+b），除非该层的输入值x在一直一个比较小的范围内。

  其实梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题，可以考虑用ReLU激活函数取代sigmoid激活函数。另外，LSTM的结构设计也可以改善RNN中的梯度消失问题。

131.如何解决梯度消失和梯度膨胀?

  （1）梯度消失：
  根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话，那么即使这个结果是0.99，在经过足够多层传播之后，误差对输入层的偏导会趋于0
  可以采用ReLU激活函数有效的解决梯度消失的情况
  （2）梯度膨胀
  根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都大于1的话，在经过足够多层传播之后，误差对输入层的偏导会趋于无穷大
  可以通过激活函数来解决

132.推导下反向传播Backpropagation

  @我愛大泡泡，来源：http://blog.csdn.net/woaidapaopao/article/details/77806273

  反向传播是在求解损失函数L对参数w求导时候用到的方法，目的是通过链式法则对参数进行一层一层的求导。这里重点强调：要将参数进行随机初始化而不是全部置0，否则所有隐层的数值都会与输入相关，这称为对称失效。 

  大致过程是:

  1.首先前向传导计算出所有节点的激活值和输出值， 

  2.计算整体损失函数： 

  3.然后针对第L层的每个节点计算出残差（这里是因为UFLDL中说的是残差，本质就是整体损失函数对每一层激活值Z的导数），所以要对W求导只要再乘上激活函数对W的导数即可 

 

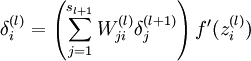
133.SVD和PCA

　　PCA的理念是使得数据投影后的方差最大，找到这样一个投影向量，满足方差最大的条件即可。而经过了去除均值的操作之后，就可以用SVD分解来求解这样一个投影向量，选择特征值最大的方向。

134.数据不平衡问题

　　这主要是由于数据分布不平衡造成的。解决方法如下：

• 采样，对小样本加噪声采样，对大样本进行下采样

• 进行特殊的加权，如在Adaboost中或者SVM中

• 采用对不平衡数据集不敏感的算法

• 改变评价标准：用AUC/ROC来进行评价

• 采用Bagging/Boosting/ensemble等方法

• 考虑数据的先验分布

本期思考题：

135.简述神经网络的发展 

在评论区留言，一起交流探讨，让更多小伙伴受益。

参考答案在明天公众号上公布，敬请关注！

往期题目：

BAT机器学习面试1000题系列（第1~60题）

BAT机器学习面试1000题系列（第61~100题）

BAT机器学习面试1000题系列（第101~105题）

BAT机器学习面试1000题系列（第106~110题）

BAT机器学习面试1000题系列（第111~115题）

BAT机器学习面试1000题系列（第116~120题）

BAT机器学习面试1000题系列（第121~125题）

BAT机器学习面试1000题系列（第126~130题）

 【关注本公众号，点击菜单“有奖游戏”，答题抽奖】

---

---

课程咨询｜微信：julyedukefu

七月热线：010-82712840