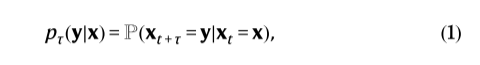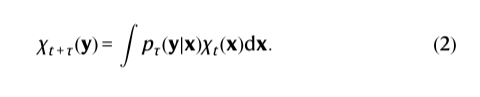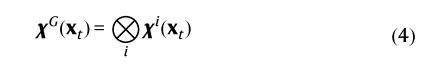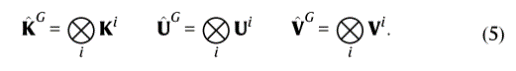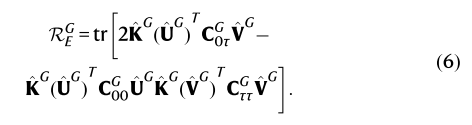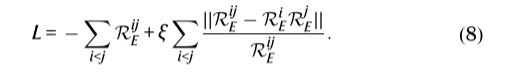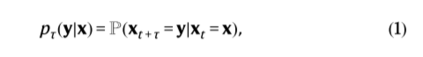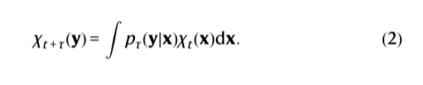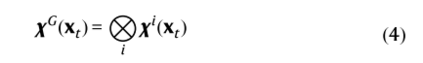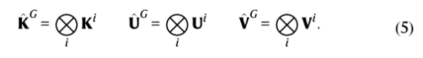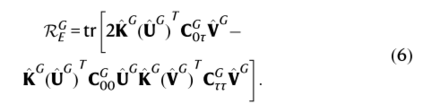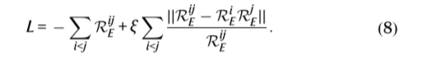Nat. Commun. | 深度学习将大分子分解为独立的马尔可夫域

编译 | 杨千立 审稿 | 陈梓豪 指导 | 闵小平（厦门大学）

此次为大家分享的是来自Nature Communiations 上的一篇题为"Deep learning to decompose macromolecules into independent Markovian domains" 的文章，来自德国柏林自由大学、美国德克萨斯州休斯顿莱斯大学的Frank Noé团队。

对越来越大的蛋白质进行动力学建模兴趣日益浓厚，但目前缺乏收集足够的状态概率或状态间转换统计数据的能力，因为对于大分子系统，亚稳态的数量随大小呈指数增长。在本文中，作者通过引入一种方法来应对这一挑战，该方法将作者在独立马尔可夫分解 (IMD) 方面的最新进展与VAMPnets (一种用于马尔可夫建模的深度学习方法) 相结合。作者建立了一个训练目标，该目标量化了基于马尔可夫动力学将分子系统分解为独立子域的程度与整体动力学的近似程度。通过构建端到端学习框架，同时学习分解成这些子域及其各自的马尔可夫状态模型，从而提供数据高效且易于解释的复杂系统动力学摘要。尽管学习马尔可夫子域之间的动态耦合仍然是一个悬而未决的问题，但目前的结果是迈出了模拟数据中学习大分子复合物伊辛模型的重要一步。

介绍

对蛋白质功能的理解通常与对蛋白质动力学的理解是相互关联的。分子动力学 (MD) 模拟是在原子尺度上研究这些动力学的工具；马尔可夫状态模型 (MSM) 已应用于广泛的分子生物学问题，例如蛋白质聚集或配体结合，并且可以成为了解原子尺度上的实验数据的工具。

评估模型性能并由此对其质量进行排名，发展了特别是马尔可夫过程 (VAMP) 的变分方法。这使我们能够使用VAMPnet，该框架同时学习使分子系统降维到最能描述罕见事件过程的集体变量和 MSM变量。该框架可用于沿着这些学习到的集体变量进一步驱动 MD 模拟，还可以使用该框架来估计统计上可逆的 MSM，并结合来自实验观察结果的约束。

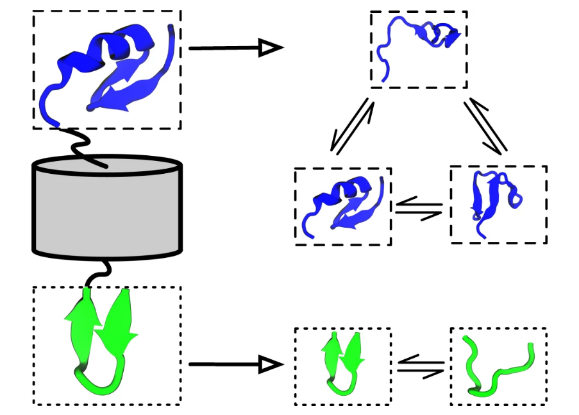
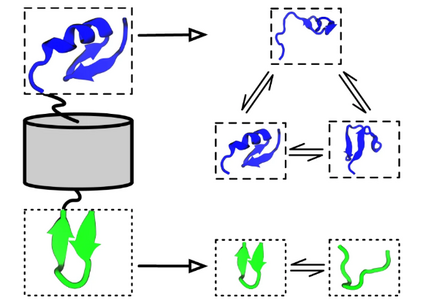
尽管有这些发展，在描述 MD 时在全局系统状态之间的转换方面存在一个基本的缩放问题：虽然小协同分子系统是一个很好的模型，但对于中小型蛋白质，较大的分子系统具有大量的的子系统，其动力学几乎独立（图 1）。例如，当这些蛋白质解离时，这些蛋白质会独立地在开放和关闭状态之间进行转换，并且这些转换仅在与其他蛋白质结合时（部分）耦合。全局系统状态的数量为2 ^N，即随着子系统数量N呈指数增长。这意味着任何形式模拟或分析都不会扩展到大分子系统。

图1：iVAMP 概念通过模拟蛋白质的动力学可视化，该蛋白质具有两个独立的柔性区域，由刚性桶隔开

同时，子系统之间的（近似）独立性也是问题解决的关键。可扩展的解决方案需要解决两个不同的问题：(a) 将蛋白质系统划分为近似马尔可夫子系统和 (b) 了解它们之间的耦合。

作者提出了一种联合 IMD(通过将全局系统动力学近似为一组独立马尔可夫模型) 和 VAMP 方法（称为iVAMPnet），它通过将IMD推广到神经网络基函数，显着提高了识别近似独立马尔可夫子系统（问题 a）的能力。iVAMPnets 是一种集成的端到端学习方法，它将大分子结构分解为动态弱耦合的子系统，并为每个子系统估计一个 VAMPnet，以促进对子系统动力学的综合分析（图1）。与之前的 IMD 相比，该方法可以学习对独立子系统的最佳分解，并且可以找到作为输入特征的非线性组合的集体变量。

结果

马尔可夫状态模型和库普曼模型

马尔可夫动力学可以通过过渡密度建模：

这是假设系统在时间t处于配置x时在时间t  +  τ时观察配置y的概率密度。基于过渡密度，我们可以将概率密度 χ 的时间演化描述为：

通过以合适的方式离散化分子状态空间并定义离散状态之间的过渡矩阵T，我们可以将此方程线性化为：

这是马尔可夫状态模型的方程，其中向量χt  +  τ(y)的元素i是在时间 t  +  τ 处于离散状态i的概率。此外，转移矩阵元素描述了给定的跳转到状态j的转移概率时间 τ 内的状态i。在模糊状态分配的情况下，例如，与 VAMPnets 一样，等式(3)描述了更一般的库普曼模型和Tτ库普曼矩阵。这意味着概率密度仍在传播，但矩阵元素不能解释为转移概率。

滞后时间 τ 是所有马尔可夫模型所共有的，通常是在隐含的时间尺度测试的帮助下选择的。如果选择的 τ 太小，则生成的模型不是有效的马尔可夫模型（导致预测变量的错误）;选择的 τ 太大会丢弃动力学信息的模型。因此，通常选择最小的滞后时间，在该滞后时间之上隐含的时间尺度近似恒定。

现在寻求找到满足方程式的状态分配χ和模型矩阵T。形式上，χ是（最初未知的）基函数，即假设相关的动态特征可以用它们的线性组合来表示。VAMP 表明，当χ可以跨越左和右奇异函数(ψ1, . . . ,ψk)T,(φ1, . . . ,φk)T的转换运算符。它们可以通过从模拟数据估计的矩阵最大化奇异值来找到(参见“方法”中的等式(9)-(13))。在VAMPnet的情况下，通过最大化 VAMP 分数来训练深度神经网络，以表示最佳模糊状态分配。在平衡状态下，奇异函数对应马尔可夫状态模型的特征函数，奇异值对应其特征值。由于库普曼模型仍然传播密度，检查T的特征函数和隐含时间尺度是有用的，因为它们描述了给定系统的慢动力学。

iVAMPnets and iVAMP-score

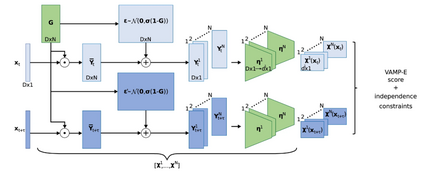
为了实现 iVAMPnets，需要弥合 VAMPnets 的深度神经网络与独立马尔可夫模型的空间分解之间的差距。总体思路是建立多个并行的 VAMPnets，每个模型都对分子的一个单独、独立的子系统的马尔可夫动力学进行建模，以及识别这些子系统的注意力机制。因此，每个独立的 VAMPnet只接收代表其特定子系统的时间依赖性分子几何特征。例如，这种注意机制可以分离不同的蛋白质域，并将各个域的数据引导到单独的 VAMPnets。因此，(图2) iVAMPnet 旨在同时优化这两个目标。

图2：适用于N个子系统的iVAMPnet体系结构，其中可训练的部分呈绿色阴影

在实践中，提取所有分子几何特征 (距离、接触等)，并将它们传入图2所示的体系结构。数据通过注意力机制 (由矩阵G表示) 馈送，该机制产生子系统特定向量Yti ，每个都涉及与子系统i相关的特征。然后，这些向量充当N个并行特征变换 ηi (并行VAMPnets) 的输入，这些变换转换为输出特征 χ1，…… χn (具有 χi (xt)= ηi (Yti (xt)))，表示直接模糊分配到每个分子子系统的亚稳态马尔可夫状态。配备了状态分配，我们可以计算相关矩阵(公式9)，并从这些矩阵(公式10)导出库普曼模型矩阵。与VAMPnets一样，特征转换 η1……ηn由深度神经网络表示。在本研究中，使用具有表示模糊状态分配的SoftMax输出层的多层感知器。更详细地说，给定N个单独的子系统模型，全局系统状态可以由所有子系统状态的Kronecker乘积给出:

并通过使用χG从等式(9)计算全局相关矩阵(C00G,C0τG,CττG)，注意到，这一步骤并不要求拥有独立的马尔可夫模型，但它只是用局部状态的组合来表达全局状态的一种形式。

此外，可以通过将单个奇异值和向量与Kronecker乘积相结合，从子系统模型中构造全局库普曼模型的候选者。

矩阵U^G和 V^G将全局状态分配映射到构造的奇异函数上，并根据等式(11,12)中定义的局部矩阵进行计算。对角矩阵K^G编码奇异值，并通过公式10从子系统奇异值矩阵中计算。

为了评估构造模型的性能以预测全局状态空间中的动力学，可以利用VAMP-E验证得分。

Vamp-E得分估计了库普曼模型与真实动力学之间的差异。在这里，它被评估为映射在构造的奇异函数(编码为U^G ,V^G)上的全局状态分配 ⨂ χi (以(C00G,C0τG,CττG)编码。如果子系统是独立的，则构造的奇异函数是最优的，并且全局系统的奇异值确实是子系统的奇异值的乘积。在这种情况下，全局VAMP-E评分公式6具有如下形式：

这为子系统独立性提供了必要条件。为了最终训练模型，作者开发了一个损失函数，该函数有两个作用，(1)使全局VAMP-E得分最大化 (2)最小化了惩罚这些子系统之间的统计依赖性的项 (式7)，由加权因子 ξ 缩放。

仅成对地评估分数，以避免全局状态空间的增长，并对所有可能的对i，j求和。

在这里，REij利用公式6量化构造的子系统i和j的库普曼模型的质量，。加权因子 ξ 是一个超参数，应选择大到足以找到解耦系统，而小到足以不干扰子系统动力学。即使选择合适的 ξ 取决于动力学和耦合的性质，它也与训练过程直接相关，因为它在动力学和解耦之间平衡了优化器的重点。评估奇异函数和值的独立性的其他条件 (式18) 可以用作训练后的验证指标，以调整 ξ 并测试发现动态独立的子系统的程度。

具有两个独立子系统的基准模型

在图2中描述了使用PyTorch实现的iVAMPnet架构。作者选择具有多达5个隐藏层的全连接前馈神经网络，每个隐藏层具有100个节点。

作者首先证明iVAMPnets能够使用精确可分解的基准模型，基于观测到的轨迹数据，将动态系统分解为其独立的马尔可夫子系统 (图3)。

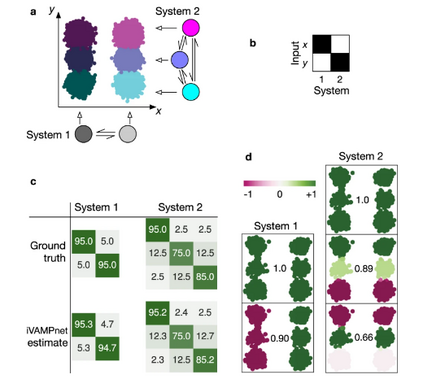
图3：隐马尔可夫状态模型作为独立子系统的基准示例

类似于图1所示的蛋白质，定义了一个系统，该系统由两个独立的子系统组成，分别具有两个、三个状态。它由两个具有相应状态数的转移矩阵建模，用每个矩阵 (100k步) 采样离散轨迹。全局状态定义为这些离散状态的组合。离散子系统状态现在被解释为隐马尔可夫模型的隐藏状态。每个子系统的输出都使用高斯噪声N~(μi,σ)建模，该高斯噪声特定于系统状态 (由指定μi) 和常数 σ。因此，两个状态子系统分别描述了沿x轴的高斯盆地和沿y轴的三个状态子系统之间的跳跃过程 (图3a)。这些变量与图1中描述的绿色 (x) 和蓝色 (y) 系统的集体变量进行比较。请注意，尽管在此基准系统中已知相关的慢速集体变量，但iVAMPnets通常能够找到它们 (参见10D超立方体基准模型和Synaptotagmin-C2A)。

由于生成基准模型由完全独立的子系统组成，并且该对已经描述了全局系统，因此作者的方法可以简单地针对全局VAMP-E得分 (等式6) 进行优化，而无需任何进一步的约束。在 τ = 1步的滞后时间训练具有两个和三个状态子系统的模型。

经过训练后，iVAMPnet会生成每个已识别子系统中的动力学模型。正如预期的那样，发现两个子系统的估计转移矩阵与基本事实非常吻合 (图3c)。为了更详细地评估慢速子系统动力学，借鉴了MSM分析的概念，并对iVAMPnet模型 (参见VAMPnets) 进行了特征值分解。对本征函数的分析表明，通过构造，系统表现出沿x轴的一个独立过程 (λ1 = 0.90) 和沿y轴的两个过程 (λ2 = 0.89和 λ4 = 0.66) (图3d)。相比之下，注意到，在全局状态的图片中，由于混合了独立的过程 (参见补充说明2)，将出现两个额外的过程，这使得组合动力学模型的分析更具挑战性，而iVAMPnet分析仍然简单明了。

除了动态模型外，iVAMPnet还会在输入特征和子系统之间分配。该方法分别正确地将两个状态系统识别为x轴，将三个状态识别为y轴特征 (图3b)。

10D超立方体基准模型

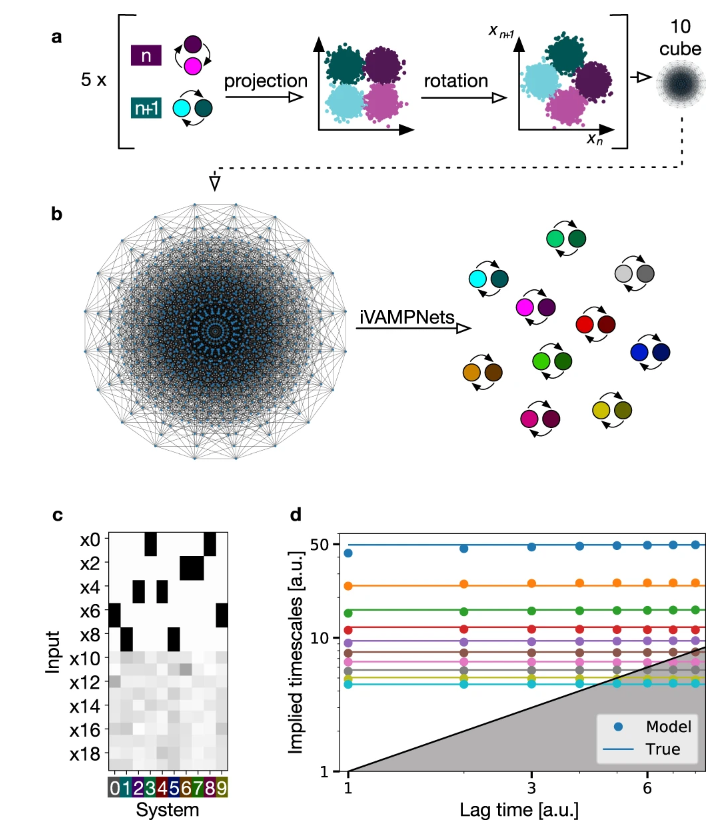
在下一步中，用十个两状态子系统测试iVAMPnet方法，其对应于1024个全局状态 (图4a，b)。与以前一样，动力学系统是由具有唯一时间尺度的十个独立的隐马尔可夫状态模型生成的。该系统被分成五对子系统，并且控制每对过渡动力学的两个坐标被旋转，以使它们更难以分离 (图4a)。此外，通过添加十个噪声维度来使学习问题变得更加困难，从而使全局系统在嵌入20维空间中的10维超立方体上。

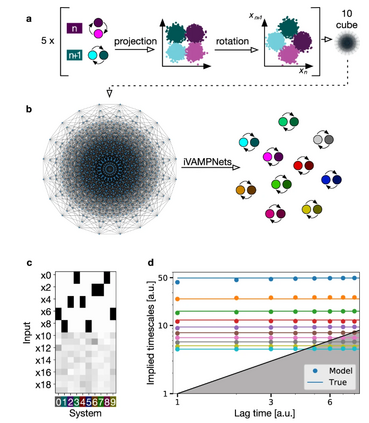
图4 ：隐马尔可夫状态模型，具有1024个全局状态，形成嵌入20D空间中的10D超立方体

尽管子系统是完全独立的，但作者将以成对的方式估计具有vamp-E分数的iVAMPnet，从而避免在R1024 × 1024中有极大的相关性。因为这只有在所有系统都是独立的情况下才是合理的，所以另外强制执行等式(7)。在训练过程中，通过最小化等式(8)，从而排除任何两个子系统近似相同的过程。

iVAMPnet估计产生子系统模型，可以通过测试其隐含的松弛时间尺度是否收敛于模型滞后时间 τ 来验证。结果表明，由iVAMPnet学习的隐含时间尺度被正确地转换并准确地再现了基本事实 (图4d)。注意到，除了由iVAMPnet识别的各个子系统的时间尺度之外，全局模型还将包含由特征值乘积产生的所有时间尺度，从而产生1024个时间尺度。因此，与全局MSM或VAMPnet相比，iVAMPnet分析提供了一个更简单，更简洁的模型。

此外，子系统分配掩码指示该方法正确地为每个模型的两个输入特征分配高重要性权重 (图4c)。因此，该方法证明了其能够以数据高效的方式将嘈杂的高维全局系统分解为其独立的子过程的能力。

作者已经将10-cube系统推广到可变数量的子系统 (N-cube) 来进行性能基准测试，发现iVAMPnets在此特定系统的性能优于VAMPnets。但是注意到，因为N-cube具有真正独立的2状态子系统，该结果可能无法推广到任意系统。

突触结合蛋白-C2A

最后，在全原子蛋白质系统上测试iVAMPnets。与基准示例相比，期望底层的全局动态系统只能近似地分解为独立的子系统。我们测试一下数据由先前描述的(补充说明7)数据组成; 突触蛋白在神经递质释放的调节中起着至关重要的作用。它被证明由近似解偶联的子系统组成，分别包含钙结合区 (CBR) 和 C78环。

首先，作者尝试使用全局模型对蛋白质进行建模，即使用单个（常规）VAMPnet。事实上，这种方法失败了，因为没有足够的模拟统计数据来估计所有全局亚稳态之间的可逆连接过渡模型，从而导致隐含的时间尺度不同（补充说明 3和补充图 2）。这正是 iVAMPnets 应该提供优势的场景，它只依赖于本地而不是全局融合的转换统计数据。

接下来，作者训练 iVAMPnet 以分别寻找12个和6个状态的两个子系统，每个子系统的滞后时间为τ  = 10 ns，强制执行等式7寻找非耦合子系统。

训练好的 iVAMPnet 识别一个包含所有三个 CBR 循环(CBR-1、CBR-2、CBR-3；图 5a)的子系统。第二个子系统不仅包括上述 C78 环路，还包括连接 β 折叠，C34环路。当映射蛋白质结构上的残基位置时，很明显这两个子系统在物理上很好地分离(图5a)，支持两个区域仅弱耦合的结论。

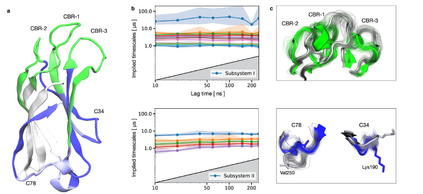
图 5：突触结合蛋白-C2A 的 iVAMPnet 具有两个子系统，分别具有12个和6个状态。

两个系统的隐含时间尺度在模型滞后时间τ中大致恒定。大多数时间尺度都在 1~10 μs 的范围内，除了在第一个子系统中是100 μs (图 5b)，这是以前没有发现的。对控制此过程的结构变化的分析表明，它涉及所有 CBR 循环的协调转换（图 5c）。然而，之前的研究无法解决这样的过程，在该研究中，CBR 被建模为单独的循环。第二个系统的过程涉及 C78 和 C34 循环的同时移动(图5c)。

iVAMPnets 在局部特征中发现亚稳态结构，这些结构与之前的工作中描述的结构相当。具体而言，可以在 CBR1 中找到两个不同位置的α螺旋和掩埋甲硫氨酸残基 (Met173) 的状态。在相邻的 CBR2 位点，确定了紧密结合和松散的配置，而 C78 位点具有所有三个先前描述的缬氨酸残基构象（Val250、Val255）。除了之前的研究中建模的特征外，iVAMPnets 还识别富含赖氨酸的簇 (Lys189-192) 中的动力学，该簇先前曾被报道对膜相互作用很重要。与作者之前的工作相比，局部子系统中的动力学模型更复杂，包含更多的动态过程，提供更全面的画面，无需手动定义分区。事实上，同时进行域分解和局部动力学建模已经能够识别非常细微的动力学特征，只要它们对局部 VAMP 分数有显着贡献。

尽管在稀疏数据样本的情况下估计突触结合蛋白的全局 VAMPnet 模型不可行，但 iVAMPnet 可以有效地使用相同的数据并估计统计上有效的动态模型。这一结果尤其引人注目，因为 iVAMPnet 方法还通过分离动态独立的蛋白质域简化了后续解释模型的任务。

反例：绒毛蛋白微型蛋白的折叠

最后，作者以时间长度25 μs 绒毛蛋白折叠轨迹作为反例进行了实验(补充说明7)。绒毛蛋白等小蛋白通常是协同的，即与折叠相关的最慢过程涉及所有残基(补充说明5)。因此，当将系统分解为多个子系统时，无法解决这些过程。事实上，作者发现分裂成两个具有两个状态的子系统，各自导致不收敛的时间尺度，并且其松弛过程近似于不相交区域上的部分折叠(参见补充图 6)。

测试学习到的动态子系统的统计独立性

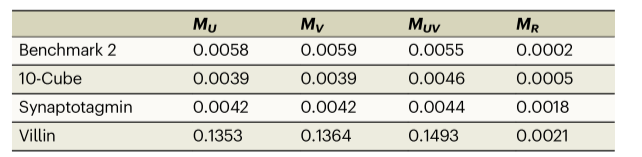
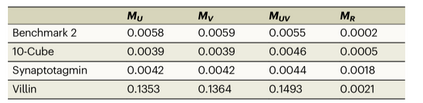
等式7在训练期间被用作惩罚，通过评估在训练期间未强制执行的约束(等式17)来评估估计子系统分配的有效性。训练独立性分数MU、 MV和MUV(在等式 18中定义)。较低的MU和MV意味着构造的左右奇异函数确实是全局状态空间中奇异函数的有效候选者。较低的MUV表明子系统模型的克罗内克积很好地预测了全局状态空间中的动力学。结果表明这三个指标非常适合指示学习子系统的独立性（表 1）。在经过测试的系统中，只有villin不能拆分成独立的部分（所有分数 > 0.1）。相比之下，基准模型和突触结合蛋白可以分解为统计上不耦合的子系统（所有分数 < 0.01）。突触结合蛋白的MR值略有增加表明其子系统可能是弱耦合的。 表1.训练后独立性验证

总结与讨论

作者提出了一种无监督的深度学习框架，该框架仅使用分子动力学模拟数据，学习将复杂的分子系统分解为行为近似独立的马尔可夫模型的子系统。因此，iVAMPnet 是一个端到端的学习框架，可以解决对模拟数据呈指数增长的需求，而模拟数据需要对越来越大的生物分子复合物进行采样。具体来说，作者已经开发并展示了用于分子动力学的 iVAMPnets，但原则上，该方法也适用于不同的应用领域，例如流体动力学。具体实现，如输入向量χt的表示和χ-功能的神经网络架构，取决于应用程序，可以根据需要进行调整。

现在有一个越来越强大的模型层次结构，从 VAMPnets 上的 MSMs 到 iVAMPnets。MSM 总是由状态空间分解和控制这些状态之间动态的马尔可夫转移矩阵组成。VAMPnets 为 MSM 提供深度学习框架，从而学习最佳状态空间离散化的集体坐标。iVAMPnets 还学习将分子系统物理分离为子系统，每个子系统都有自己的慢坐标、马尔可夫状态和转移矩阵。

作者已经证明 iVAMPNets 是一种强大的多尺度学习方法，当这些子系统确实在统计上独立进化时，它可以成功地找到和建模分子子系统。此外，iVAMPnets 能够从高维 MD 数据中学习。为了证明这一点，已经证明突触结合蛋白 C2A 域可分解为两个几乎独立的马尔可夫状态模型。重要的是，已经证明突触结合蛋白 C2A 的这种动态分解是成功的，而尝试使用全局马尔可夫状态模型对系统进行建模由于采样不佳而失败。这直接证明 iVAMPnets 在统计上比 VAMPnets、MSM 或其他全局状态模型更有效，并且确实可以扩展到更大的系统。

然而，注意到，iVAMPnets 不学习子系统如何耦合，因此在它们当前的形式下，仅适用于由非耦合或弱耦合子系统组成的分子系统。虽然已知大多数生物分子复合物是协同的，但也有使用独立子系统非常成功地建模的示例。耦合程度是一个有争议的问题，例如突触结合蛋白中的 C2 串联(C2A和C2B 结构域)。由于已知孤立域在许多情况下会自行发挥作用，作者认为丢弃耦合是适合识别这些域及其相关亚稳态的一阶建模假设。

跟进参考并引入描述学习的 MSM 如何耦合的耦合参数，这是正在进行的研究。此外，弱耦合假设是针对所研究分子过程的时间尺度做出的，可能无法推广到任意时间。

除了深度学习方法中通常的超参数选择外，iVAMPnet 还需要指定所寻找子系统的数量。这种选择可以通过为不同数量的子系统训练 iVAMPnet 然后询问独立性分数（等式18、19) 选择统计独立性最佳的分解。建议首先将系统分解为两个子系统作为起点，然后增加这个数量。例如，反映在不收敛的隐含时间尺度(可能是抽样问题的化身，可以通过增加子系统的数量来缓解)或高独立性分数(不可能拆分系统)。此外，子系统数量的选择可以由蛋白质中的结构域数量或使用参考文献中介绍的基于网络的方法来指导。此外，每个子系统中的状态数量需要平衡 (a) 奇异函数近似的质量（少数状态更高）和 (b) 模型分辨率（更多状态更高）。最终，不同的选择可能会产生收敛的验证措施，并且在这种情况下可以选择状态的数量来产生所需的模型分辨率。

可以通过多种方式改进和进一步开发 iVAMPnet，例如，通过采用更高级的网络架构，例如图形神经网络，其中参数可以跨子系统共享。这可能会导致更高质量的模型和对超参数选择的更强鲁棒性。最近，图神经网络确实成功地与 VAMPnets 相结合，表明所得到的方法 (GraphVAMPnets) 适用于 MD 数据，并且估计模型是高质量的。

总之，iVAMPnets 为以数据高效和可解释的方式对大型生物系统的动力学进行建模铺平了道路。

方法

文章中有关的数学公式定义、推导在该部分中，感兴趣的朋友可以访问原文进一步学习。

参考资料 Mardt, A., Hempel, T., Clementi, C. et al. Deep learning to decompose macromolecules into independent Markovian domains. Nat Commun 13, 7101 (2022). https://doi.org/10.1038/s41467-022-34603-z

项目地址 https://github.com/markovmodel/ivampnets