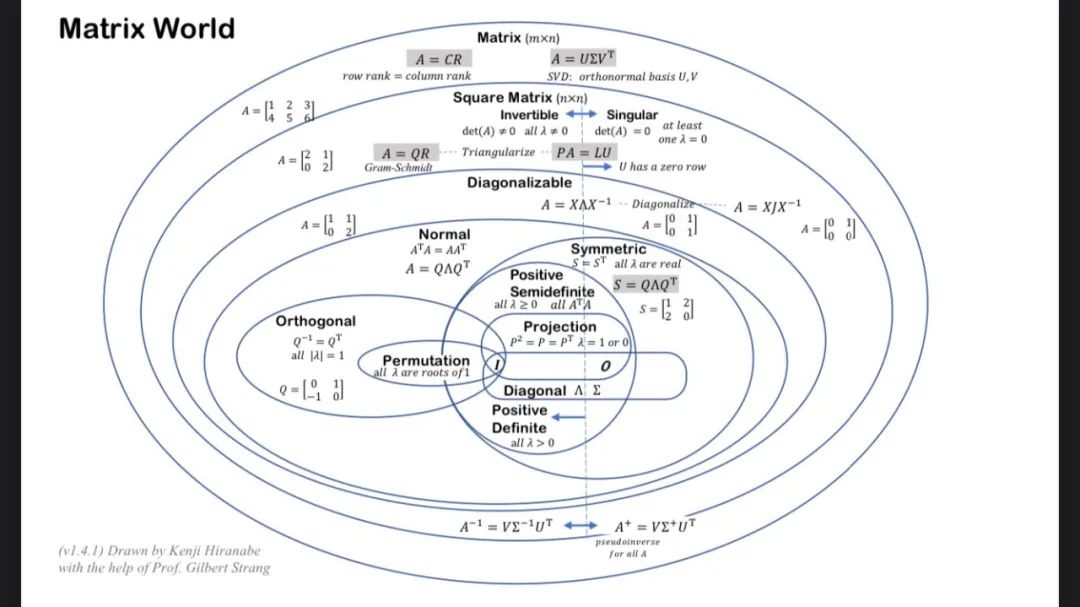
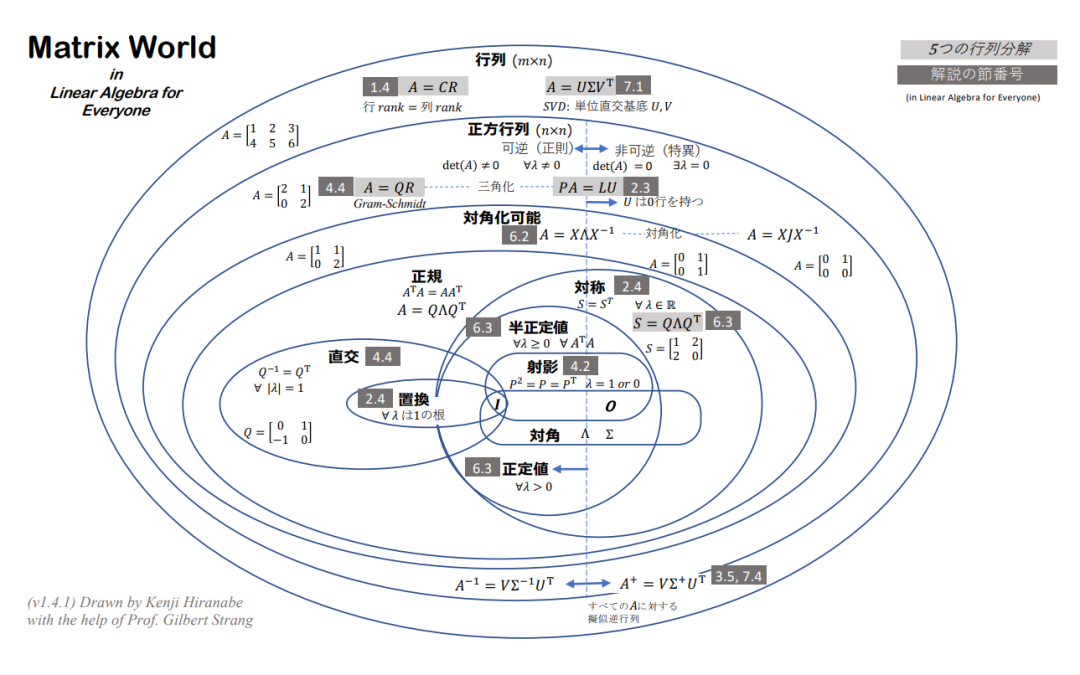
来自MIT Gilbert Strang教授的矩阵经典图解,收藏!
85岁MIT教授Gilbert Strang《线性代数》2020视频课,不怕学不会的线代
本笔记试着用直观的方式把《线性代数》中介绍的重要概念表达出来本课程旨在从矩阵分解的角度促进对向量/矩阵计算和算法的理解。它们包括列行(CR)、高斯消去(LU)、Gram-Schmidt正交化(QR)、特征值与对角化(QΛQT)和奇异值分解(UΣV T)。
https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra
成为VIP会员查看完整内容
相关内容
专知会员服务
393+阅读 · 2021年1月11日
Arxiv
0+阅读 · 2022年10月2日
Arxiv
0+阅读 · 2022年10月1日