如何理解信息论？伯克利最新《信息论》图文导论，43页pdf概述信息论中的熵、不确定、熵、互信息、编解码等基础概念

虽然信息论最初是为通信工程而发展的，但它包含了数学工具，在科学和工程中有许多应用。这些工具可以用来描述存在噪声时数据压缩和传输的基本限制。在这里，我们提出了一个对信息论的实用的指南。我们的综述只假设你熟悉基本概率论。

在20世纪40年代，Claude Shannon[1]证明了信息的精确数学定义直接来自于概率公理。从那时起，信息理论通过定义数据压缩的极限和在嘈杂的网络中可靠地传输数据，成为我们今天生活的数字世界的基础。此外，它提供的数学工具在不同的领域，如统计、机器学习、密码学、量子计算、生物学和许多其他领域都有大量的应用。在这里，我们介绍信息论的基础，重点是直觉。这是对关键思想的一个最低限度的介绍。在优秀的教科书[2,3]以及Shannon的原始配方[1]中可以找到更全面的处理方法。

在信息论的语境之外，我们大多数人对“信息”是什么已经有了一个模糊的直观概念，它通常是接近于“对未知事物获得的知识”的东西。信息论的主要进步之一是将这种直觉形式化，变成数学上精确的东西。香农自己曾经说过:“信息可以被当作一个物理量，比如质量或能量。”香农通过用概率来定义信息，从而使信息的概念在数学上具体化。如果发送者向接收者发送某物的信息，那么该信息所描述的是不可预测的事情。换句话说，从接收者的角度来看，这是随机的。信息论表明，信息的随机性(其特征是潜在信息的概率分布)实际上是弄清楚如何传输信息的唯一重要因素。消息的实际内容无关紧要。

在信息理论中有两个关键问题将在接下来的章节中出现。第一个是源编码，它涉及数据压缩:给定一个随机事件源，平均而言，我们在如何简洁地记录随机序列的结果方面有什么限制?这可以进一步细分为两种情况，一种是原始序列可以在解压后完美重构(无损压缩)，另一种是可以容忍原始序列的某些失真以实现更小的数据大小(有损压缩)。第二个问题是与数据传输有关的信道编码:给定一个随机事件的来源，以及一个不完善的信息传输系统(一个有噪声的信道)，我们如何对这样的事件序列进行编码，使它们对信道引入的错误具有鲁棒性?再次，我们可以细分为完美数据传输和带错误的数据传输。

目录内容：

信息，不确定性，熵和互信息 什么是信息 熵与数据压缩 冗余 数据压缩极限 互信息 条件熵 熵和互信息之间的关系 随机过程的熵率 概率密度和微分熵 率失真理论 通道 通道编码

信息，不确定性，熵和互信息

*什么是信息？

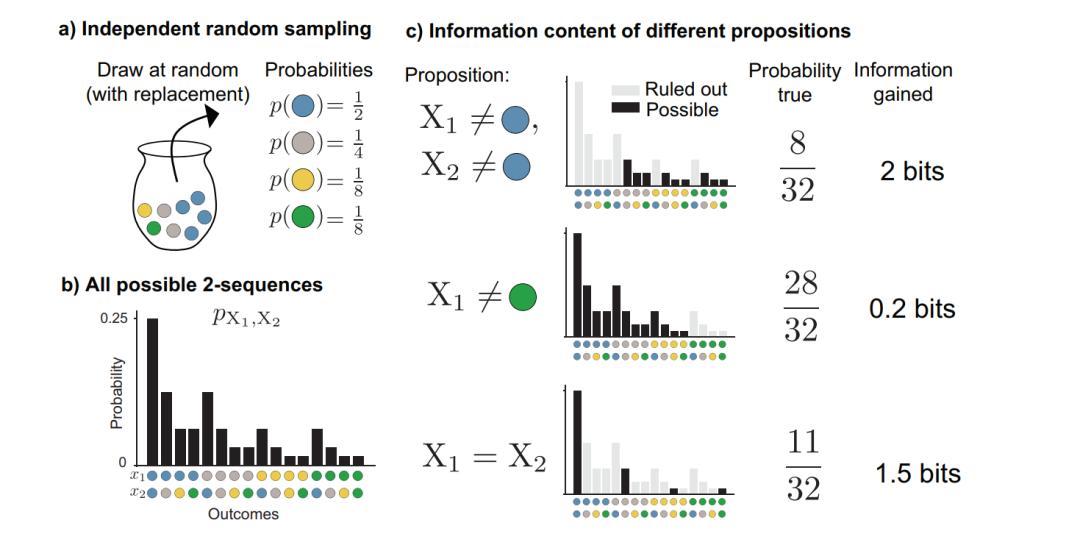
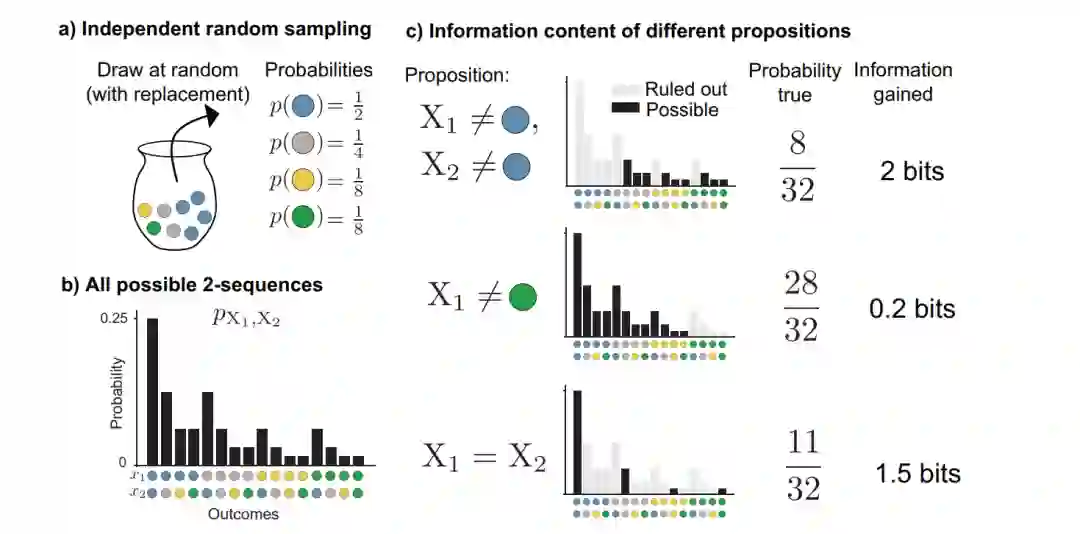
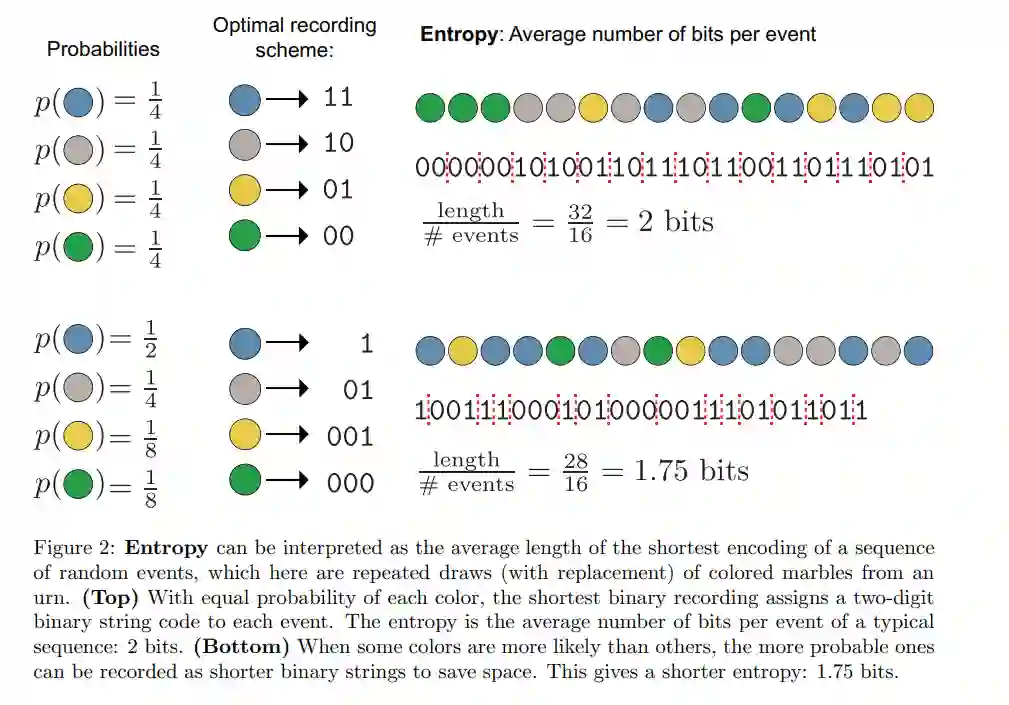
不确定性、随机性和信息缺乏是看待同一潜在想法的不同方式。如果我们不能预测事件的结果，我们就是不确定的，从我们的角度来看，它是随机的。然而，我们也许能够获得关于事件的信息，减少其表面上的随机性，使我们对它更确定。3小时后天气会怎么样?这是不确定的。但从现在到那时，我们可以通过观察当前的天气来持续获取信息，从现在开始的3小时内，我们的不确定性将崩溃为零。它对我们来说不再是随机的。天气预报并不是唯一符合这种模式的领域。事实上，信息论表明，所讨论的随机事件的几乎所有特征都与它的信息内容是分离的——重要的是它的概率分布。因此，我们可以在一般随机事件的背景下考虑信息论:从一个装有蓝色、绿色、黄色和灰色弹珠的瓮中反复随机抽取一颗弹珠。(图1)。

概率和信息的等价性

熵和数据压缩

随机变量的熵与许多其他有趣的性质有关。例如，它量化了可以实现的大量(无损)数据压缩的极限，这是信息论中被称为源编码的问题。

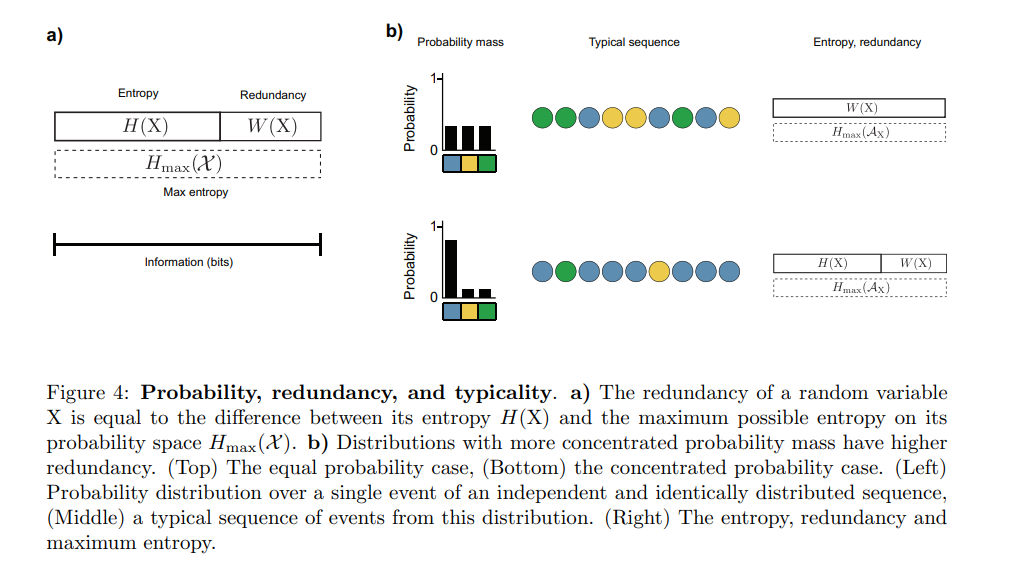
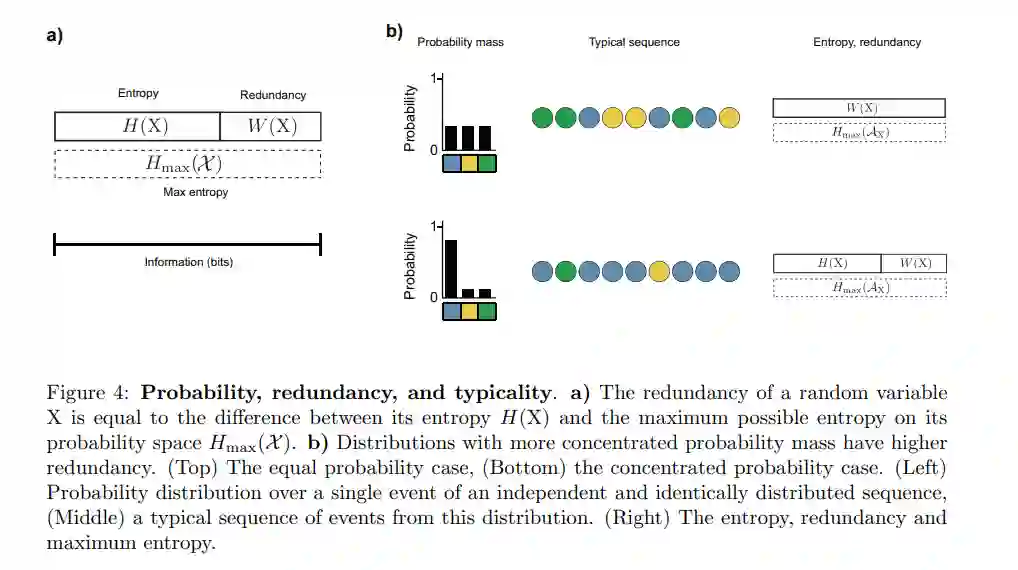
冗余

一个随机事件的冗余取决于其结果的不确定性程度，与同一个概率空间上的变量的不确定性程度相比。

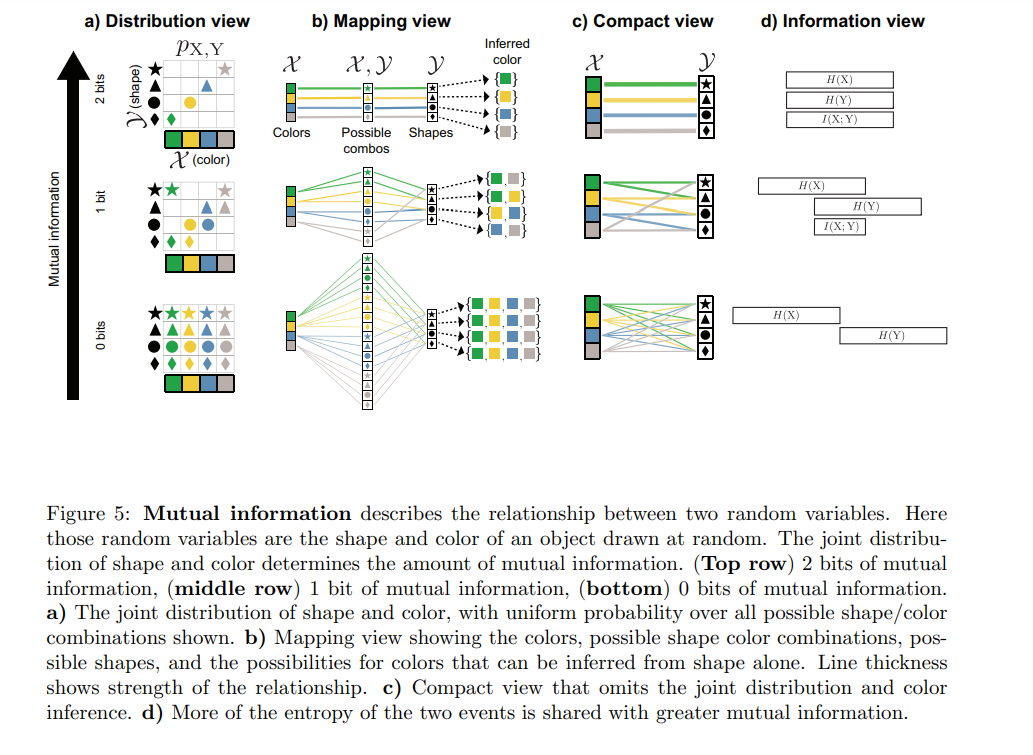
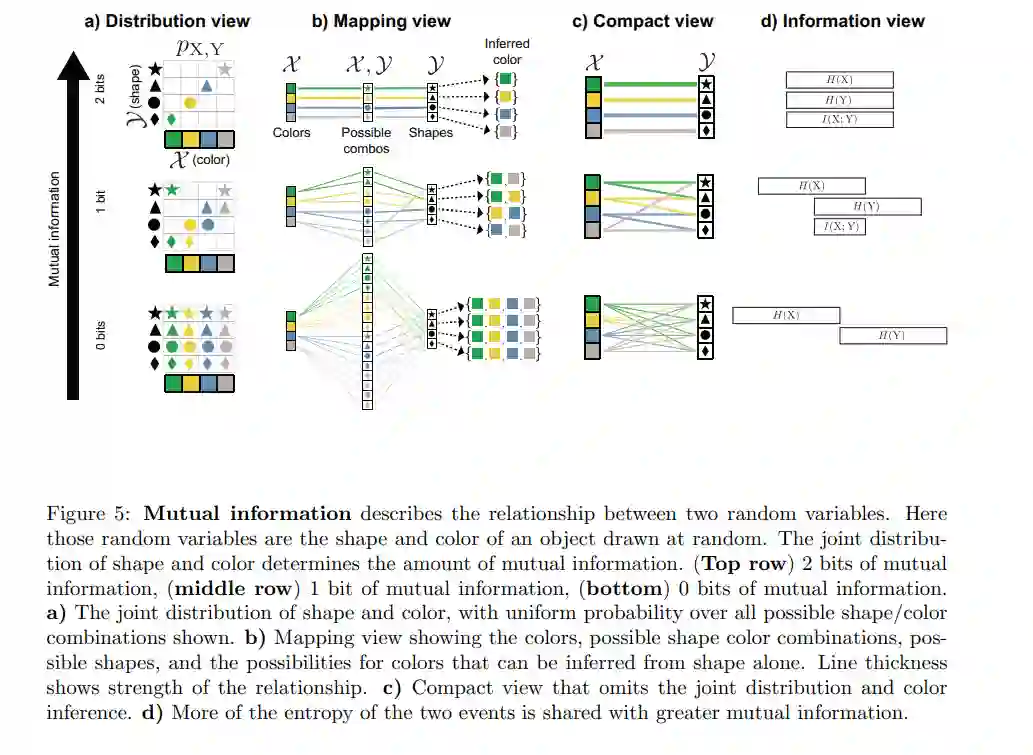
互信息

在描述了如何量化一个随机事件的信息内容之后，我们现在考虑更一般的情况，即信息如何在多个随机事件之间共享—也就是说，通过知道另一个随机事件的结果，如何减少一个随机事件的不确定性。这为推断和计算信息的传递提供了基础。