GNN如何用于因果推断？TU&DeepMind-AAAI2022投稿论文《关联图神经网络与结构因果模型》阐述基于GNN的因果推理

【导读】图神经网络与因果推理是当下大家关注的焦点，GNN有强大的图结构建模表达能力，因果推理旨在探究因果关系结构，如何将两者联系起来是一个挑战性的问题？来自TU&DeepMind的研究人员将这两者做了研究，建立基于GNN的因果推理。

因果性可以用结构因果模型(SCM)来描述，该模型承载了有关兴趣变量及其机械关系的信息。对于大多数感兴趣的过程来说，底层的SCM将只是部分可见的，因此因果推理试图利用任何观察的信息。图神经网络(GNN)作为结构化输入的通用逼近器，为因果学习提供了一个可行的候选者，建议与SCM更紧密的集成。为此，我们提出了从第一原理出发的理论分析，在GNN和SCM之间建立了新的联系，同时提供了一般神经因果模型的扩展观点。然后我们建立了一个新的基于GNN的因果推理模型类，该模型类是因果效应识别的必要和充分条件。我们对模拟和标准基准的实证说明验证了我们的理论证明。

https://www.zhuanzhi.ai/paper/8c09c90940b1603f6d6dbce7335df3fc

引言

理解因果关系是人类认知的核心，因此对科学、工程、商业和法律具有很高的价值(Penn and Povinelli 2007)。发展心理学向我们展示了孩子们是如何像科学家一样进行探索的，都是通过问“如果……会怎么样?””和“为什么?这类问题((Gopnik 2012; Buchsbaum et al. 2012; Pearl and Mackenzie 2018)，而人工智能研究梦想将科学家的行为方式自动化(McCarthy 1998; McCarthy and Hayes 1981; Steinruecken et al. 2019)。深度学习带来了可优化的逼近普适性，这是指对于任何函数都存在一个接近任意精度的神经网络(Cybenko 1989;Hornik 1991)。这种能力已经在各种应用中获得了巨大的成功(Krizhevsky, Sutskever, and Hinton 2012;Mnih et al. 2013;Vaswani et al. 2017)。因此，将因果关系与深度学习相结合，对于即将达到人类智能水平的研究具有至关重要的意义。对所谓的神经-因果模型进行紧密整合的初步尝试(Xia et al. 2021;Pawlowski, Castro, and Glocker 2020)的存在，并显示出有望实现一个系统的梦想，该系统在其最令人印象深刻的应用中，可以执行与现代神经模块同样规模的有效性的因果推理。

虽然因果关系在过去十年中已经被彻底地正式化了(Pearl 2009;Peters, Janzing, and Scholkopf 2017)，“另一方面，深度学习在实际应用中取得了成功，理论突破仍然很少。”Bronstein等人(2017)率先提出了几何深度学习的概念，从几何观点出发并将其推广到现代架构的一类重要神经网络是图神经网络(GNN) (Velickovi ˇ c et al. 2017; Kipf and Welling 2016a; Gilmer ´ et al. 2017)。与其他专门的神经网络类似，GNN在药物发现(Stokes et al. 2020)和谷歌地图的ETA预测(DerrowPinion et al. 2021)等专门应用中取得了最先进的性能。这些特性，我们称之为归纳偏差，可以利用其他证明不可能的推论(Gondal et al. 2019)。

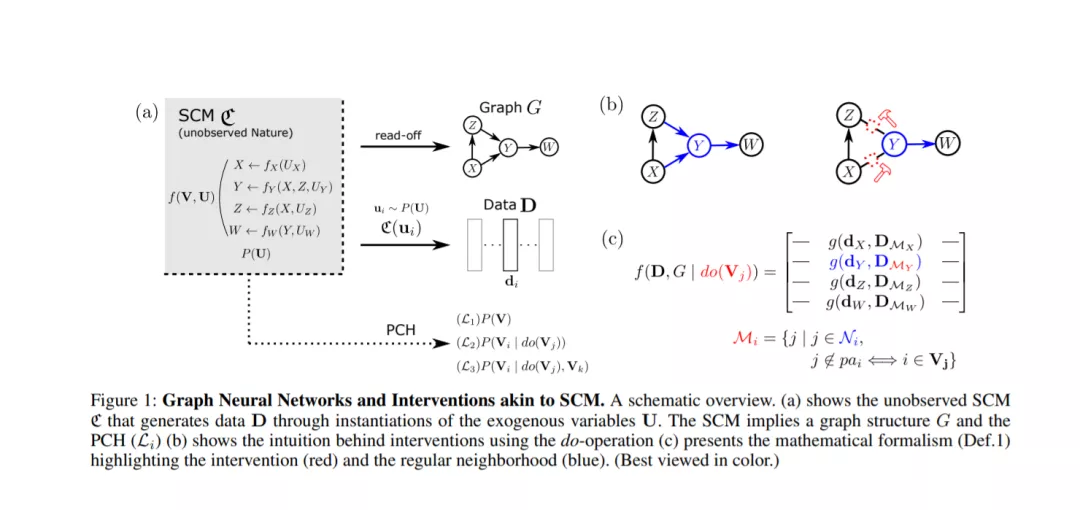
顾名思义，GNN在输入的结构上放置了一个归纳偏差，即，输入的维度是相关的，这样它们就形成了一个图结构。要回到因果关系，其核心是结构因果模型(SCM)，它被认为是负责数据生成的现实模型。SCM在其所建模的变量上暗示了一个图结构，而由于GNN研究的是图，对这两个模型之间的关系进行更仔细的检查似乎对神经因果人工智能的研究进展是合理的。我们没有从因果关系的原则中获得灵感来改进机器学习(Mitrovic等人，2020年)，而是展示了GNN如何用于执行因果计算，即因果关系如何在神经模型中出现。更准确地说，因果推理是指Pearl因果层次(PCH)模型(Bareinboim et al. 2020)。也就是说，我们以(部分)因果图和/或来自层次结构不同层次的数据的形式获得了关于SCM的部分知识。

总的来说，我们做出了一些关键贡献: (1) 我们从第一性原理推导出GNN和SCM之间的理论联系; (2)定义一个更细粒度的NCM; (3) 我们形式化了GNN的干预，并由此建立了一个新的神经因果模型类，利用自动编码器;(4) 在与现有工作相关的情况下，我们提供了关于这一新的模型类的可行性、表达性和可识别性的理论结果和证明。(5) 我们实证检验了我们的理论模型在识别和估计任务中的实际因果推理。