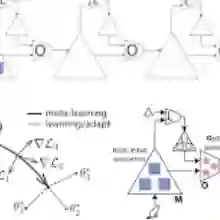
基于深度元学习的因果推断新方法
Bengio, Yoshua, et al. "A meta-transfer objective for learning to disentangle causal mechanisms." ICLR (2020).
引言
因果推断是统计学领域的重要技术,主要通过观测到的统计量判断各个变量之间的因果关系。该技术在众多学科,尤其是在医学和经济学中得到了广泛关注和应用。
理论上讲,要想判断两个变量之间有无因果关系,最理想的方法是通过对照实验。例如,要想判断某种药品对病人是否有效,只需在“用药组”和“对照组”之间进行对照实验即可。进行这样的实验,需要保证两组病人之间除了对照变量之外完全一致。然而,这一条件在现实生活中,常常无法达到。例如,判断性别是否对某种疾病有影响,难道要让病人做变性手术吗?而在更多时候,由于实验成本太高,回顾性的分析才是主流。
另一方面,传统统计学里,用来描述统计量之间因果关系的,往往是最简单的线性模型。当然,针对简单的问题,高相关性的线性模型就足以预示两者之间的因果关系。但这对于实际问题来说,显然是远远不够的。
针对这两个问题,Bengio组在今年的ICLR上发表了文章 A Meta-Transfer Objective for Learning to Disentangle Causal Mechanisms,提出了一种全新的基于元学习和深度神经网络的因果推断模式。
背景
因果推断离不开对照实验,而计算机科学中从来没有对照实验。因此,在该文章中,作者首次提出了用元学习(Meta learning) 代替昂贵的对照实验的想法。
用元学习的一系列迁移数据集代替对照实验
众所周知,在元学习中,我们往往拥有一系列相似但不同的数据集,并希望我们的模型可以拥有良好的泛化能力,也就是在这些数据集上都能取得良好的效果。在因果推断中,便可以假设这些数据集都是某种对照实验的结果,只是该对照试验改变的变量(Intervention)是未知的。
那么,既然不知道这些数据集中哪些条件出现了变化,又该如何判断数据集中不同变量之间的因果关系呢?该文章中提出了一个重要的论断,该论断成为了后文所有推导的基石:
基于正确的因果关系设计的模型,其在迁移数据集下的收敛速度要快于基于错误的因果关系设计的模型。
简单的例子:患病-用药 实例
假定这样一个数据集:数据集中有两个变量 (是否患病,是否用某种药),且两个变量的取值均为 0(否)或 1(是)。通过极大似然法,我们可以很容易地估计两个变量之间的联合概率:
| p(患病,用药) |
|
| p(不患病,用药) | p(不患病,不用药) |
以及这两个变量的相关性。
很显然,我们无法得知这两个变量之间的因果关系。无论你假设这两个变量哪个是原因哪个是结果,联合概率分布都不会有区别(这是一个直观的事实,具体证明及实验详见原论文附录)。当然根据常识,我们可以知道是因为患有某种疾病,才会去用药的。
然而,如果我们有另一个数据集呢?在上帝视角里,这第二个数据集里p(用药|患病)的概率和上一个数据集相同,然而p(患病)和上一个数据集不同。也就是说,第二个数据集里的人类对待患病的反应与前者相同,但疾病的发病率出现了变化。
现在,我们想要知道患病与用药的因果关系如何,便可以设计两个基于梯度的对比模型,一个基于“患病→用药”假设,先推导p(患病),再推导p(用药|患病),最后得出预测结果似然p(用药,患病|参数)。另一个恰好相反,先推导p(用药),再推导p(患病|用药),最后得出预测结果似然p(用药,患病|参数)。其中,p(患病=0) + p(患病=1) = 1,所以要表达患病的概率只需要1个 [0,1]之间的自由参数。同样地,p(用药=0|患病=0) + p(用药=1|患病=0) = 1,所以表达 p(用药|患病)的四个参数中只有两个是自由参数。一旦这些自由参数的值确定下来,那么其他的参数也可以随之确定,因为概率的加和总等于一。因此,第一个模型中一共有着3个自由参数(第二个模型也是如此)。更基本地,如果一个类似的存在两个离散变量的概率模型中每个变量有N个取值的话(在这个例子里N=2),自由变量的个数为(N - 1) + N(N - 1) = N*N - 1 。模型的优化目标则是最大化似然函数p(用药,患病|参数)。
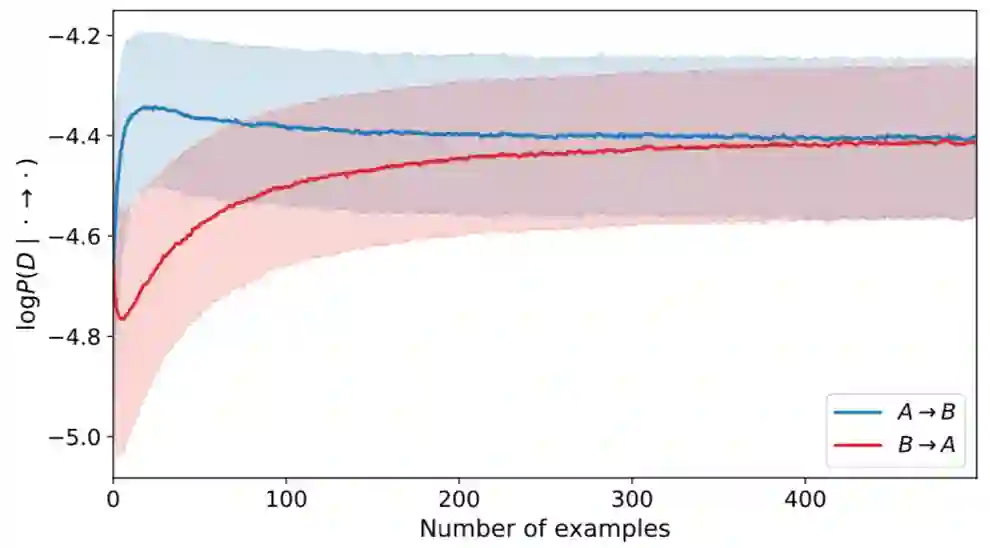
我们先将两个模型分别在同一数据集上训练好,然后将它们迁移到第二个数据集上去。显而易见,两个模型收敛后得到的似然值应该是相同的。然而,它们的训练曲线不同。如下图:
可以看出,随着见到的数据实例不断增多,两个模型最中都收敛到了相同的值。然而,正确的模型收敛更快,尤其是在模型训练的开始阶段。其中,logP(D|A→B)代表在“患病→用药”假设(正确的假设)下出现训练数据的似然的平均值,反之亦然。
为什么会这样?
文中解释说,由于正确的模型中大部分的参数都与迁移后的参数更接近,所以只需要调节更少的参数,模型就可以收敛。因此,模型收敛的速度更快,泛化性能更好。
文中还给出了这一现象更严谨的表述形式:模型(a)在原分布上充分学习,并(b)在因果关系中有正确的父节点且(c)原分布和迁移分布的条件概率相同的情况下时,将模型从原分布转移到迁移分布中时,关于模型参数的regret(迁移训练时的对数似然的积分)的期望梯度是0。并在论文附录中给出了证明。
进一步地,文中将这一推断进一步拓展到了更复杂的情况。假设数据集中每条数据有M个变量(在上面的例子中M=2),我们要学习这M个变量之间的因果关系。那么,对于其中的每对变量 (A, B),都可以设计一个参数γ,使得p(A → B) = sigmoid(γ)而p(B → A) = 1 - sigmoid(γ)。文中提出了一个优化目标
R = − log [sigmoid(γ)LA→B + (1 − sigmoid(γ))LB→A]
其中,LA→B就是我们上文用到的似然在前T步优化时的乘积。
LA→B = ΠT PA→B(at,bt;θt)
可以看出,如果因果关系A→B是正确的,那么PA→B(at,bt;θt) 和LA→B就会增大,在优化时使得γ的值增大以达到最优。这点在论文附录中也给出了证明。
为了优化γ,本文设计了一套类似元学习的训练方法。在这一方法中,模型本身的参数θ作为算法内循环的参数,在多个数据集之间共享。而表达因果关系的参数γ作为外循环的参数,对每个数据集是独特的。总体算法如下:
初始化模型中所有参数,假定所有变量都具有因果关系
初始化γ
在原分布上预训练模型
重复 J 次:
选择一个迁移分布
根据γ选择因果结构
重复 T 次:
在迁移分布上采样一个minibatch
计算它的在线对数似然
根据似然更新模型内参数
计算γ的梯度并更新
在某些情况下,将模型参数重新设置为预训练后的结果
实验
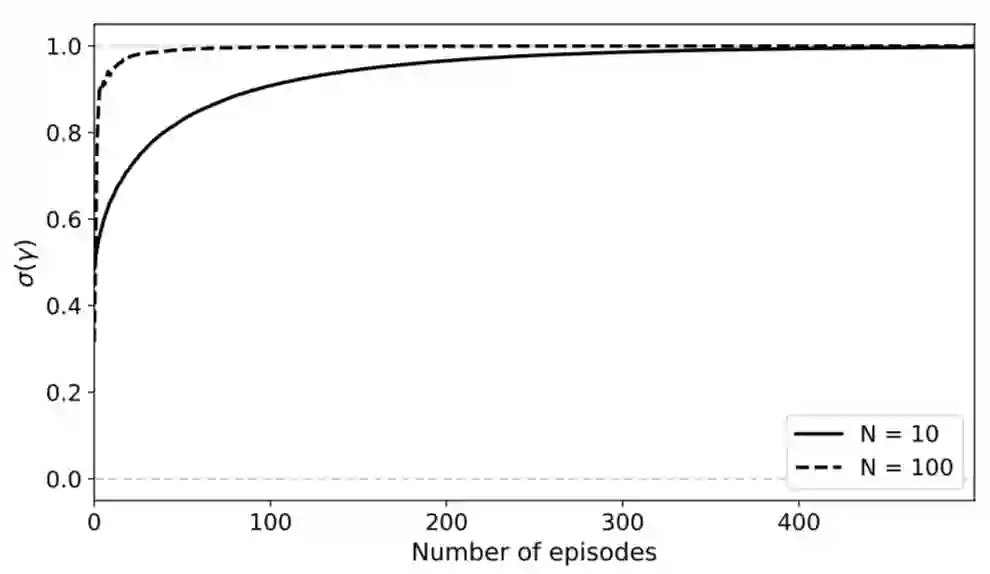
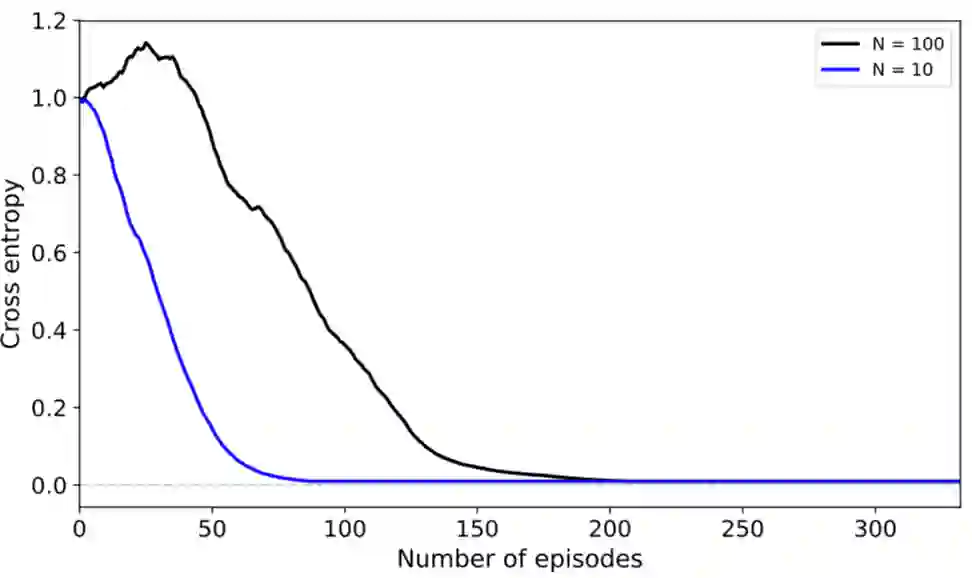
这两张图描述了在模型训练过程中,参数γ收敛的情况和模型的预测能力变化。可以看出,随着训练轮次的增加,描述因果关系的参数γ稳定地收敛到正确的结果,且随着模型训练轮次的增加,模型的预测能力也上升了。
往期文章: