等变图神经网络综述解读

作者：北邮GAMMA Lab博士生 王春辰

本文旨在介绍近年等变图神经网络的进展，参考于最新的等变图神经网络综述。 许多科学问题都需要处理几何图形的数据。不像一般的图数据，空间几何图形呈现平移，旋转和翻转的不变形。研究人员利用了这种特性设计了几何等变图神经网络(GNNs)，以更好地表征几何图形的运算和拓扑。基于必要但简明的数学基础，本文分析并将现有的方法分为三类。

1. 等变

设 和 分别是输入向量空间和输出向量空间，它们都被赋予了一组变换 和 。如果当我们对输入应用任何变换时，输出也通过相同的变换或在某种可预测的行为下发生改变，那么函数 就称为等变。在形式上， 如果函数对于G中的任何变换可交换，那么函数 就是G-等变的，，其中 和 是输入和输出空间。

群G是一组具有二进制运算 的变换，并且满足以下属性： 在关联组合下是封闭的，存在一个单位元，每个G中的元必须有一个逆。 根据群体的定义，我们在这里提供了一些例子：

• 是一个由旋转和翻转组成的n维正交群。
• 是一个特殊的正交群，它只由旋转组成
• 是一个n维的欧几里得群，它由旋转、翻转和平移组成。
• 是一个特殊的欧几里得群，由旋转和平移组成。

群表示：一个群的表示是一个可逆的线性映射 ，其中以群元素 作为输入，并作用于一个向量空间 上，同时他是线性的：。

2. 几何等变图神经网络

2.1 几何图（空间图）

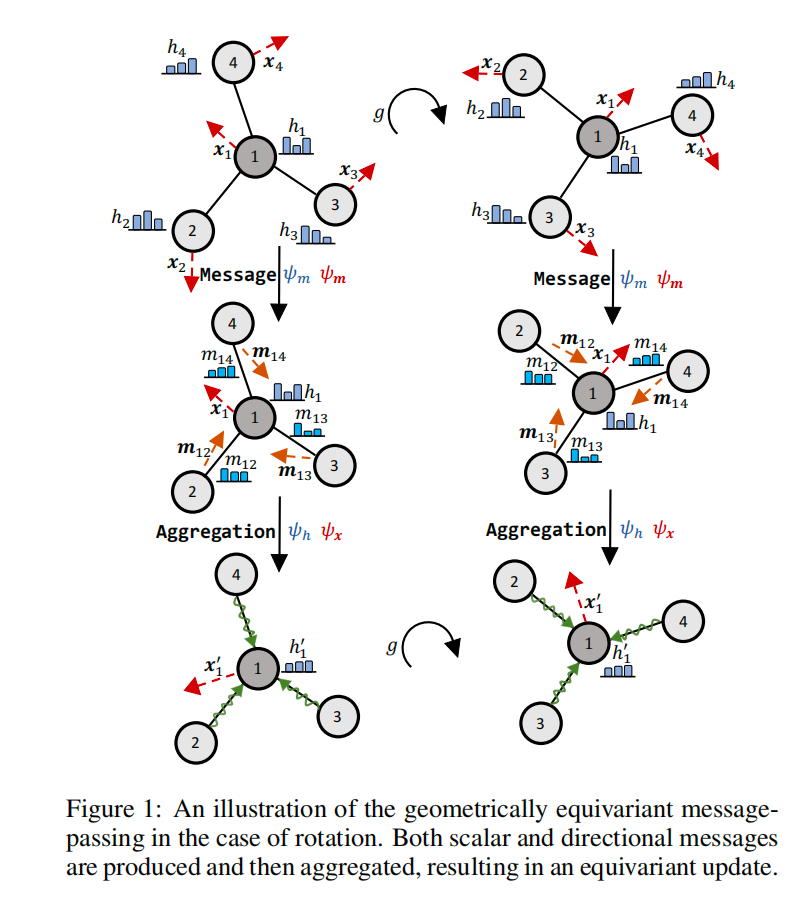
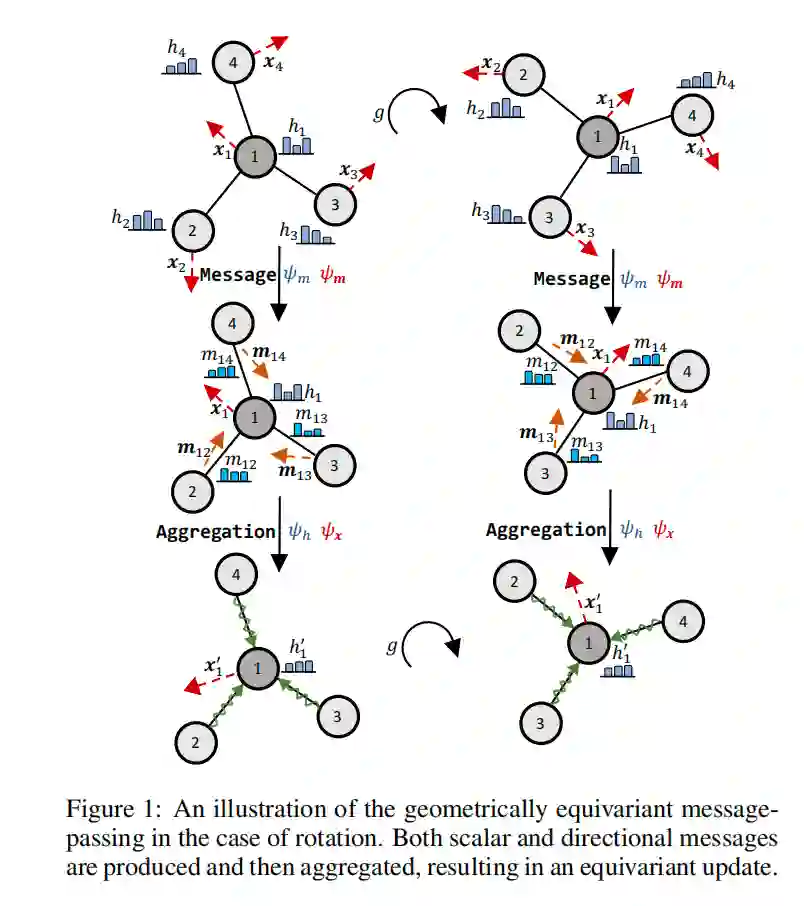
在许多使用图建模的场景中，我们处理的数据内容不仅包含拓扑连接和节点特征，也有某些几何信息。以一个药物分子为例，每个原子被分配一个标量特征 (e.g.、电 荷、质量等)，以及一个几何向量 (e.g.、位置或速 度坐标)。当通过gnn处理这类数据时，我们可以将等变的归纳偏差加入到图模型中。例如，当预测一个分子的能量时，我们需要输出是对几何向量的任何旋转不变的；然而，当预测分子动力学时，我们要求输出与每个原子位置的输入是等变的。为了更好地区分，本文中使用普通符号表示一般特征，用加粗符号表示几何特征 等变图神经网络的邻域聚合和消息传递可以归纳为：

其中，和 分别表示沿边 进行消息传递的标量输出和矢量输出， 和 分别是标量特征和几何向量的消息聚合函数。下图详细说明了上述等变消息传递协议。

下面我们将简单介绍一下三类等变图神经网络

2.2 不可约表示

根据表示理论 [Esteves，2020]，紧群的线性表示可以通过不可约表示（或简称 irreps）的直接和表示，直至相似性变换。特别是对于群 ，irrep 是 的Wigner-D 矩阵 ，其中正整数 。对于每个 表示，有 ， 其中 是 Wigner-D 矩阵， 是考虑基变化的正交矩阵， 是沿对角线的矩阵的直接和或串联。通过这种方式，向量空间被划分为l个子空间，每个子空间由 转换，并且位于第l个子空间中的向量被称为l型向量。例如，在上述几何等变图神经网络的框架中，标量 是具有 H 通道的 0 型向量，而 是 1 型向量。这些向量通过张量积 相互作用，Wigner-D 矩阵的张量积通过 CG 分解产生 Clebsch-Gordan (CG) 系数 ： 。 构建等变消息传递层的最后一个方法是球谐波 ，它用作 的等变基。通过上述构建，[Thomas et al.， 2018] 提出了满足 等方差的 TFN 层，

其中 表示节点 的几何向量的度为 ， 是节点坐标（固定在所有层上）， 是半径为 的可学习函数，过滤器 是球谐波和 CG 系数的线性组合，是自相互作用权重。

2.3 正则表示

另一个思路直接寻求使用正则表示从群卷积中获得等方差的解决方案[Cohen and Welling，2016a]，它将卷积过滤器定义为群的函数。然而，在处理连续和平滑群时，群卷积中的积分变得棘手，在这种情况下可以利用的一个可行工具是李代数。为此，[Finzi et al., 2020] 提出了 LieConv 通过提升（将 中的输入映射到群元素 ）和卷积积分的离散化来计算群卷积 通过 PointConv 技巧。特别是，通过一致的符号，LieConv 的表述如下。

其中 是 的提升，对数将每个群成员映射到作为向量空间的李代数 g 上，而 是参数 MLP。很明显，LieConv 只指定节点特征 的更新，同时保持几何向量 不变。这意味着LieConv是不变的。

2.4 标量化

除了群表示理论之外，许多工作还采用了通过标量化对等方差进行建模的通用方法。通常，几何向量首先转换为不变标量，然后通过几个MLP来控制幅度，最后在原始方向上相加以获得等方差。这个想法最初在SchNet[Schutt et al., 2018]和DimeNet [Klicpera et al, 2020]中有所暗示。Radial Field[Kohler et al.,2020] 实现了等变版本，但它只对几何向量进行操作，而不考虑节点特征。EGNN [Satorras et al.，2021b] 通过灵活的范式进一步完善了这个想法.

其中 是几何向量 和 的标量化；和 是任意 MLP。通过设置 ，EGNN 通过以等变但直接的方式联合传播节点特征 和几何向量 。

3 应用

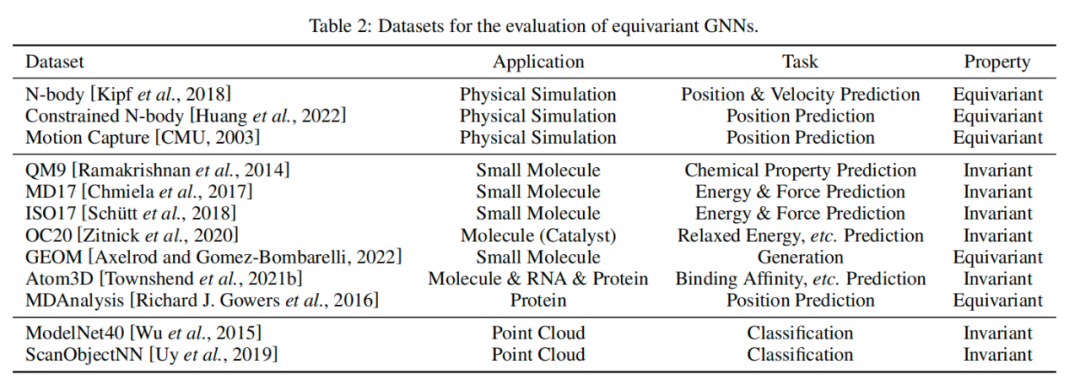
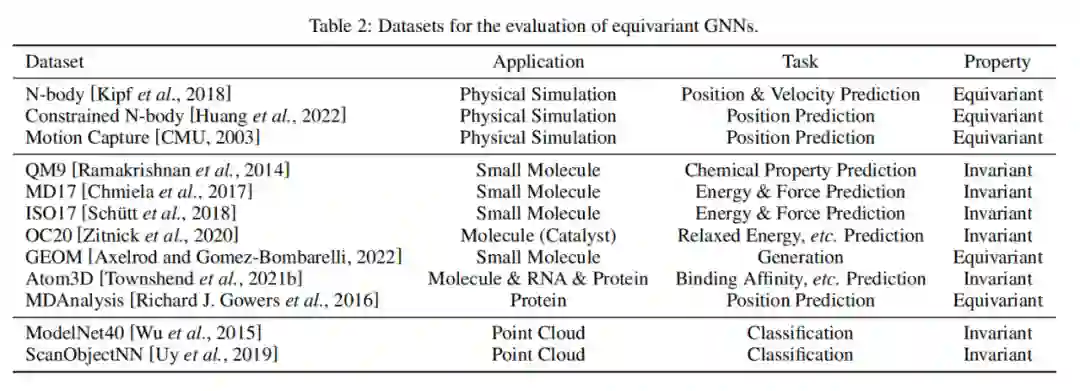
等变GNN在各种类型的现实世界几何数据中具有广泛的应用，从物理系统到化学物质。数据集资源概览如下图所示。

参考文献： [Esteves, 2020] Carlos Esteves. Theoretical aspects of group equivariant neural networks, 2020. [Thomas et al., 2018] Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, and Patrick Riley. Tensor field networks: Rotation-and translation equivariant neural networks for 3d point clouds. arXiv preprint arXiv:1802.08219, 2018. [Cohen and Welling, 2016a] Taco S. Cohen and Max Welling. Group equivariant convolutional networks. In ICML, 2016. [Finzi et al., 2020] Marc Finzi, Samuel Stanton, Pavel Iz mailov, and Andrew Gordon Wilson Generalizing con volutional neural networks for equivariance to lie groups on arbitrary continuous data. In ICML, 2020. [Sch¨utt et al., 2018] Kristof T Sch¨utt, Huziel E Sauceda, PJ Kindermans, Alexandre Tkatchenko, and K-R M¨uller.Schnet–a deep learning architecture for molecules and materials. The Journal of Chemical Physics, 148(24):241722, 2018. [Klicpera et al., 2020] Johannes Klicpera, Janek Groß, andStephan G¨unnemann. Directional message passing for molecular graphs. In ICLR, 2020. [K¨ohler et al., 2020] Jonas K¨ohler, Leon Klein, and Frank Noe. Equivariant flows: Exact likelihood generative learning for symmetric densities. In ICML, 2020. [Satorras et al., 2021b] Victor Garcia Satorras, Emiel Hoogeboom, and Max Welling. E(n) equivariant graph neural networks. arXiv preprint arXiv:2102.09844, 2021.本期责任编辑：杨成本期编辑：刘佳玮

---