摘要
我们为网络上的多智能体影响博弈提供了一种多项式时间的、可扩展的均衡计算算法,将 Bindel、Kleinberg 和 Oren (2015) 的工作从单智能体扩展到多智能体场景。在影响力博弈中,智能体具有有限的宣传预算来影响某些网络中节点对其初始倾向,但节点的最终决策取决于网络上 DeGroot 意见动态的静止状态。在多智能体系统中,智能体应该如何花费他们的预算来传播网络,以最大限度地利用它们来预测其他宣传智能体和网络动态?我们证明了这个博弈的纳什均衡是纯粹的并且(在弱假设下)是唯一的,并且可以在多项式时间内计算;我们通过使用镜像下降计算随机图上的两个智能体案例的均衡来测试我们的模型。
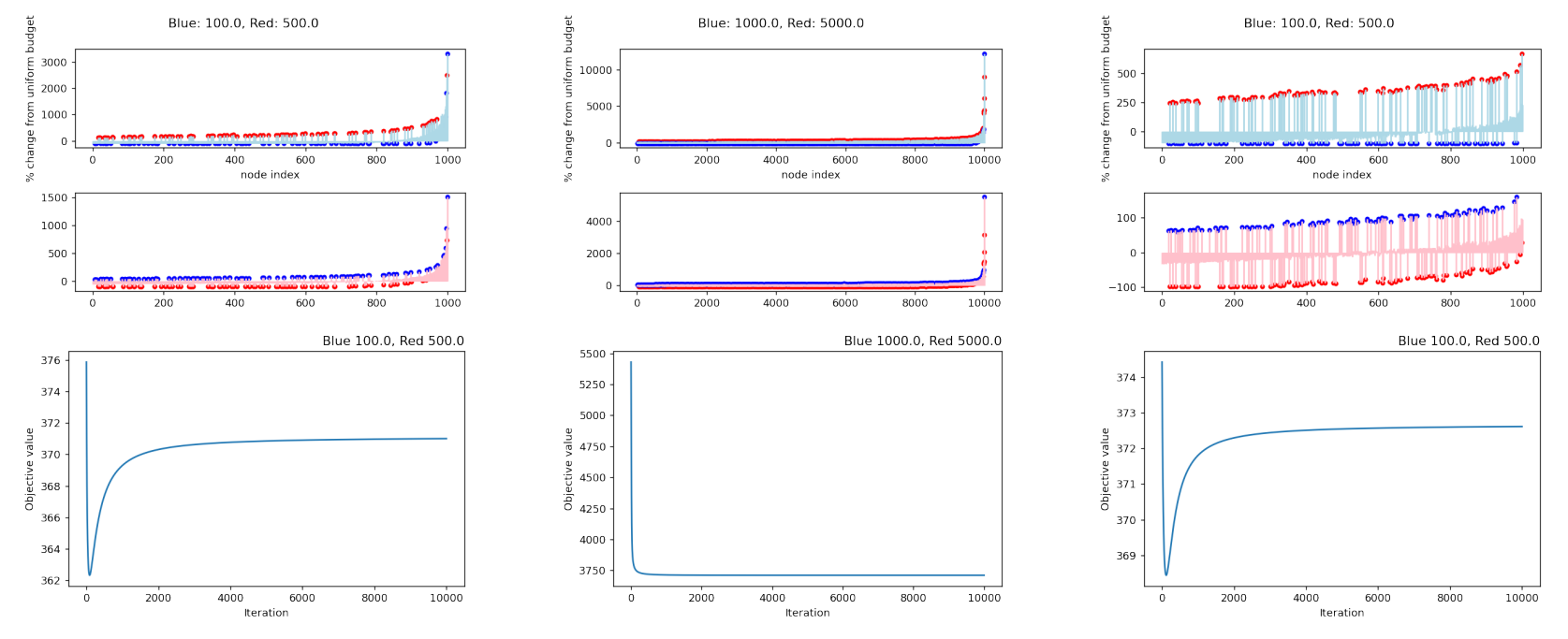
图 1:顶部图显示均衡时预算的百分比变化(来自统一策略);节点按它们在邻接矩阵的第二个特征向量中的分量排序,反映了图结构。底部图说明了均衡计算算法的收敛速度。红色和蓝色节点用点突出显示。从左到右:1000 个节点和度参数为 3 的 Barabasi-Albert 图,10000 个节点和度参数为 3 的 Barabasi-Albert 图,以及 1000 个节点,初始度为 3,重连概率为 0.2 的 WattsStrogatz 图。
成为VIP会员查看完整内容
相关内容
Arxiv
0+阅读 · 2022年4月18日