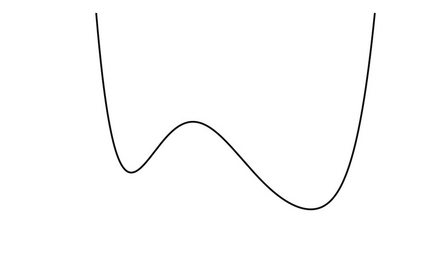
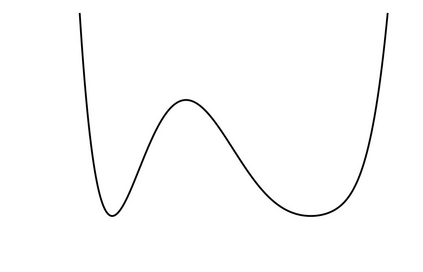
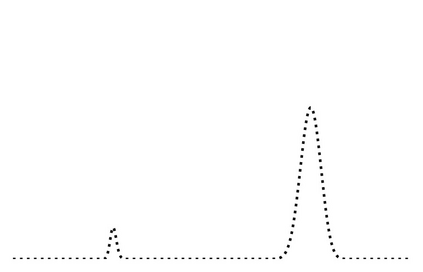
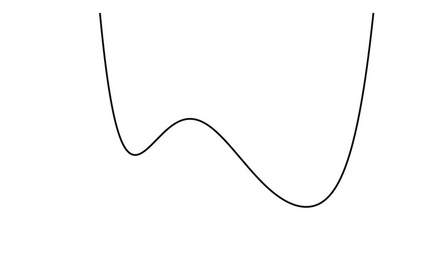
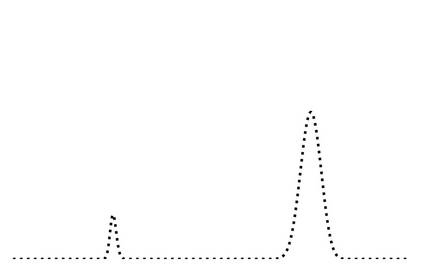
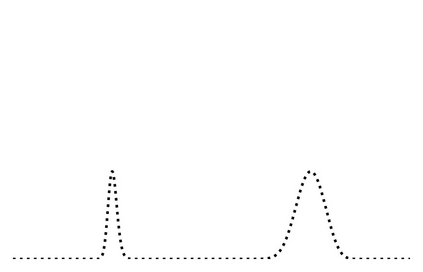
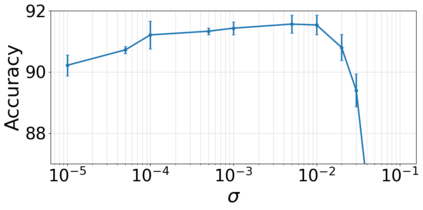
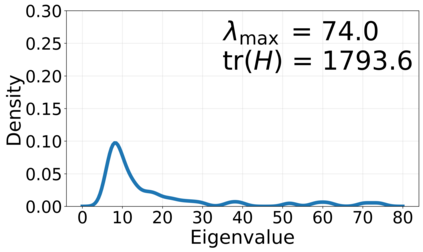
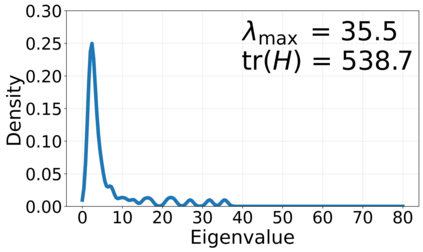
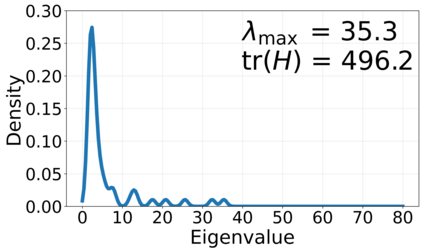
Generalization in deep learning is closely tied to the pursuit of flat minima in the loss landscape, yet classical Stochastic Gradient Langevin Dynamics (SGLD) offers no mechanism to bias its dynamics toward such low-curvature solutions. This work introduces Flatness-Aware Stochastic Gradient Langevin Dynamics (fSGLD), designed to efficiently and provably seek flat minima in high-dimensional nonconvex optimization problems. At each iteration, fSGLD uses the stochastic gradient evaluated at parameters perturbed by isotropic Gaussian noise, commonly referred to as Random Weight Perturbation (RWP), thereby optimizing a randomized-smoothing objective that implicitly captures curvature information. Leveraging these properties, we prove that the invariant measure of fSGLD stays close to a stationary measure concentrated on the global minimizers of a loss function regularized by the Hessian trace whenever the inverse temperature and the scale of random weight perturbation are properly coupled. This result provides a rigorous theoretical explanation for the benefits of random weight perturbation. In particular, we establish non-asymptotic convergence guarantees in Wasserstein distance with the best known rate and derive an excess-risk bound for the Hessian-trace regularized objective. Extensive experiments on noisy-label and large-scale vision tasks, in both training-from-scratch and fine-tuning settings, demonstrate that fSGLD achieves superior or comparable generalization and robustness to baseline algorithms while maintaining the computational cost of SGD, about half that of SAM. Hessian-spectrum analysis further confirms that fSGLD converges to significantly flatter minima.
翻译:暂无翻译