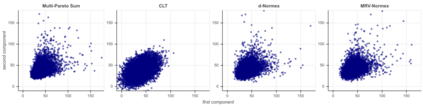
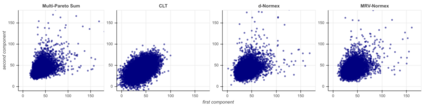
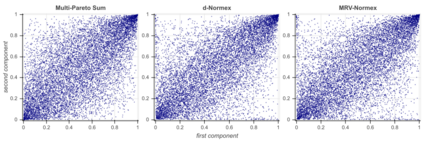
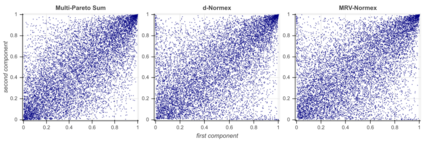
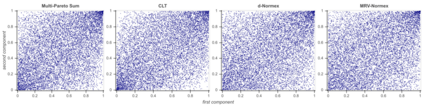
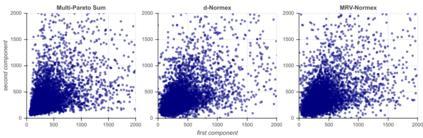
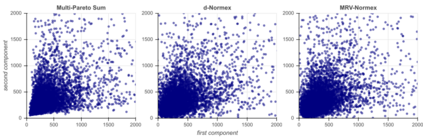
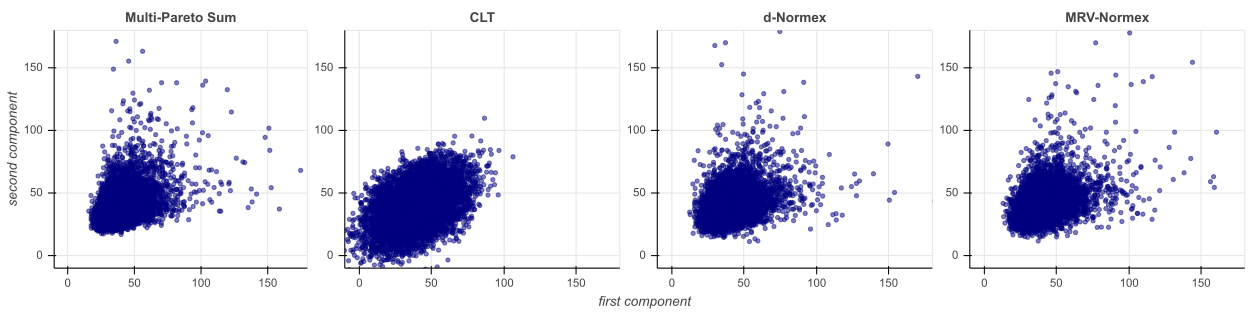
We build a sharp approximation of the whole distribution of the sum of iid heavy-tailed random vectors, combining mean and extreme behaviors. It extends the so-called 'normex' approach from a univariate to a multivariate framework. We propose two possible multi-normex distributions, named $d$-Normex and MRV-Normex. Both rely on the Gaussian distribution for describing the mean behavior, via the CLT, while the difference between the two versions comes from using the exact distribution or the EV theorem for the maximum. The main theorems provide the rate of convergence for each version of the multi-normex distributions towards the distribution of the sum, assuming second order regular variation property for the norm of the parent random vector when considering the MRV-normex case. Numerical illustrations and comparisons are proposed with various dependence structures on the parent random vector, using QQ-plots based on geometrical quantiles.
翻译:我们构建了一个对重尾随机矢量总和分布的精确近似值, 将中度和极端行为结合起来。 它将所谓的“ 诺尔梅克斯 ” 方法从一个单向框架扩展为多变量框架。 我们建议两种可能的多诺尔摩斯分布, 名为$d$- Normex 和 MRV- Normex 。 两者都依靠高斯分布来通过 CLT 描述平均行为, 而两个版本之间的差别来自使用精确分布或 EV 定理的最大值。 主要的参数为每个版本的多诺尔摩斯分布向总分布的趋同率, 假设在考虑 MRV- normex 案例时, 母向随机矢量的规范有第二顺序的常规变异属性 。 使用基于几何孔的 Q- plots, 提出了对母向量矢量的不同依赖结构的数值说明和比较。