Local conservation laws of continuous Galerkin method for the incompressible Navier--Stokes equations in EMAC form

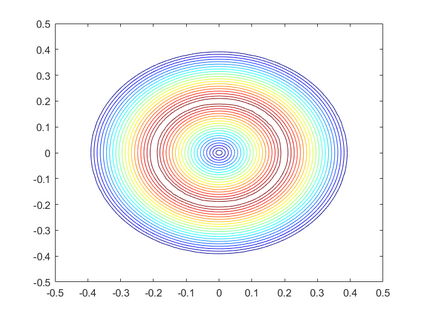
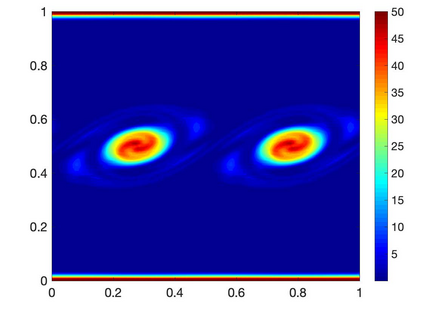
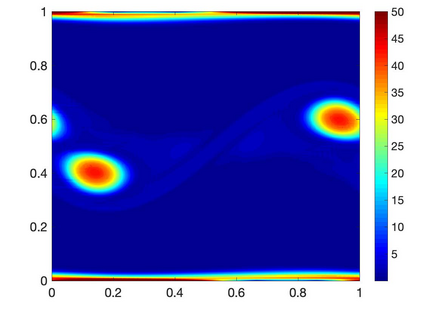
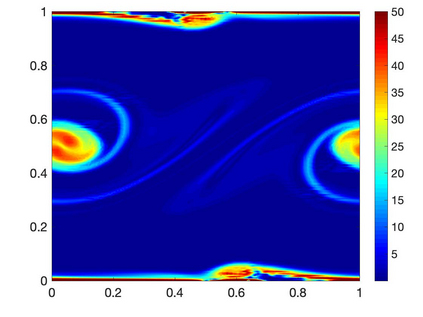
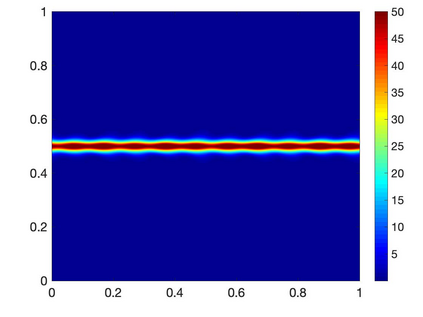
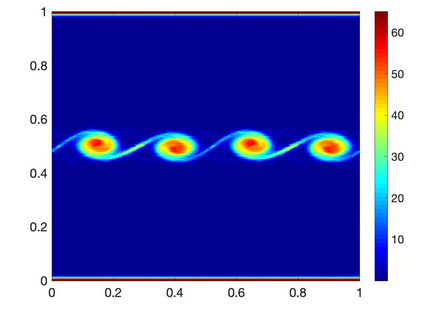
We consider {\it local} balances of momentum and angular momentum for the incompressible Navier-Stokes equations. First, we formulate new weak forms of the physical balances (conservation laws) of these quantities, and prove they are equivalent to the usual conservation law formulations. We then show that continuous Galerkin discretizations of the Navier-Stokes equations using the EMAC form of the nonlinearity preserve discrete analogues of the weak form conservation laws, both in the Eulerian formulation and the Lagrangian formulation (which are not equivalent after discretizations). Numerical tests illustrate the new theory.