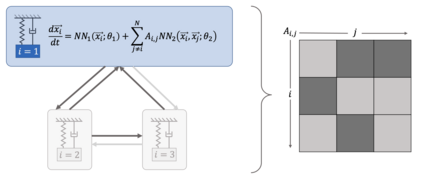
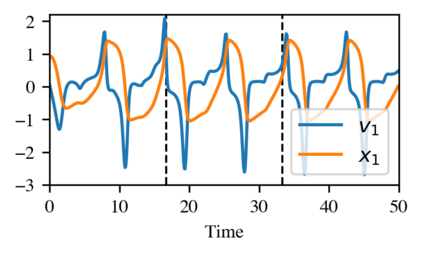
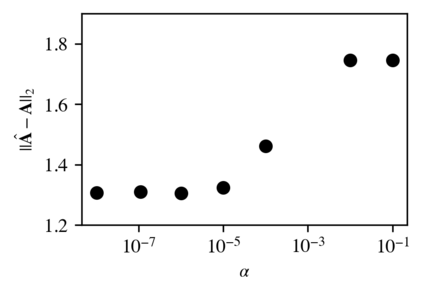
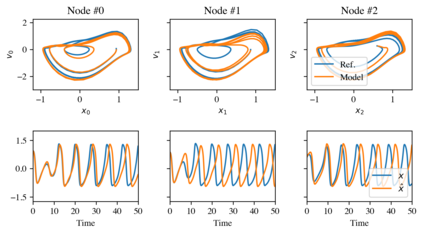
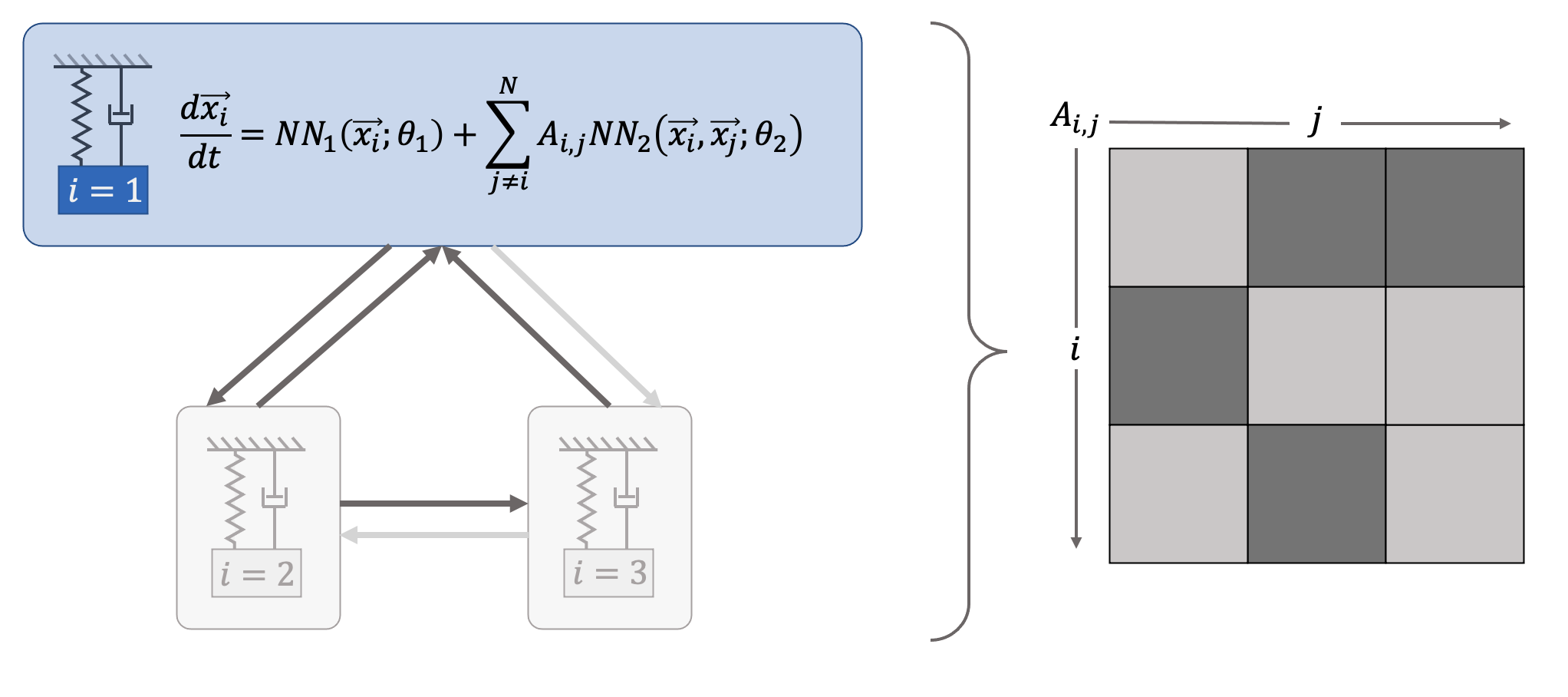
Networked dynamical systems are common throughout science in engineering; e.g., biological networks, reaction networks, power systems, and the like. For many such systems, nonlinearity drives populations of identical (or near-identical) units to exhibit a wide range of nontrivial behaviors, such as the emergence of coherent structures (e.g., waves and patterns) or otherwise notable dynamics (e.g., synchrony and chaos). In this work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies. The effectiveness and utility of these methods is shown with their application to canonical networked nonlinear coupled oscillators.
翻译:对于许多这类系统,非线性驱使同一(或近同)单元的网络动态系统群,以展示广泛的非三边行为,例如出现一致的结构(例如波浪和模式)或其他显著的动态(例如同步和混乱)。在这项工作中,我们试图推断:(一) 人口基单元的内在物理,(二) 单位之间共享的基本图形结构,以及(三) 给定网络化动态系统的混合物理学,对节点状态进行观测。这些任务围绕普遍差异方位概念来拟订,根据这一概念,未知的动态系统可以与神经网络相近,已知的前置(尽管有未知的参数)数学术语,或两者的组合。我们通过不仅调查未来状态预测,而且调查不同网络顶层的系统行为的推论,来显示这些推论任务的价值。这些方法的有效性和实用性与这些网络的实用性都展示了这些方法的运用情况。