A Faster Algorithm for Maximum Weight Matching on Unrestricted Bipartite Graphs

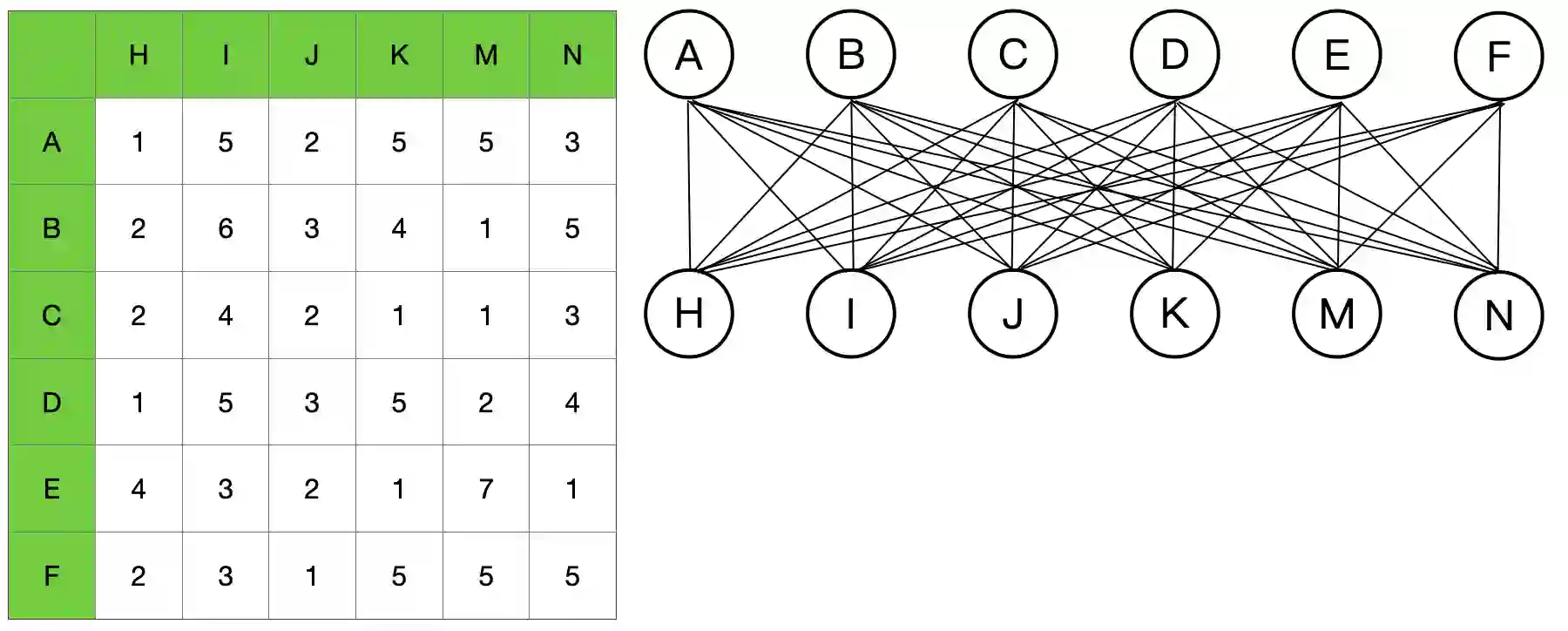
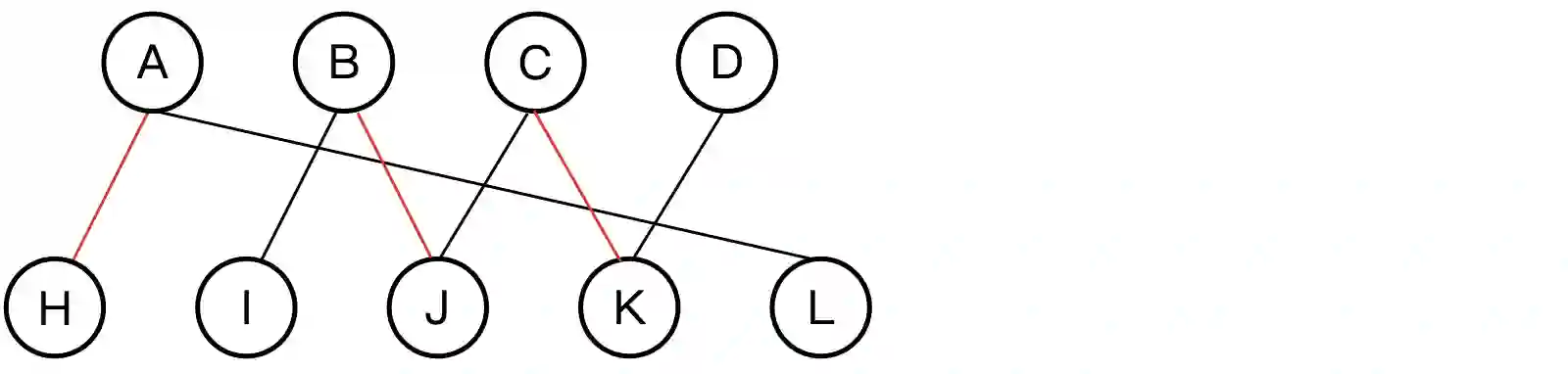
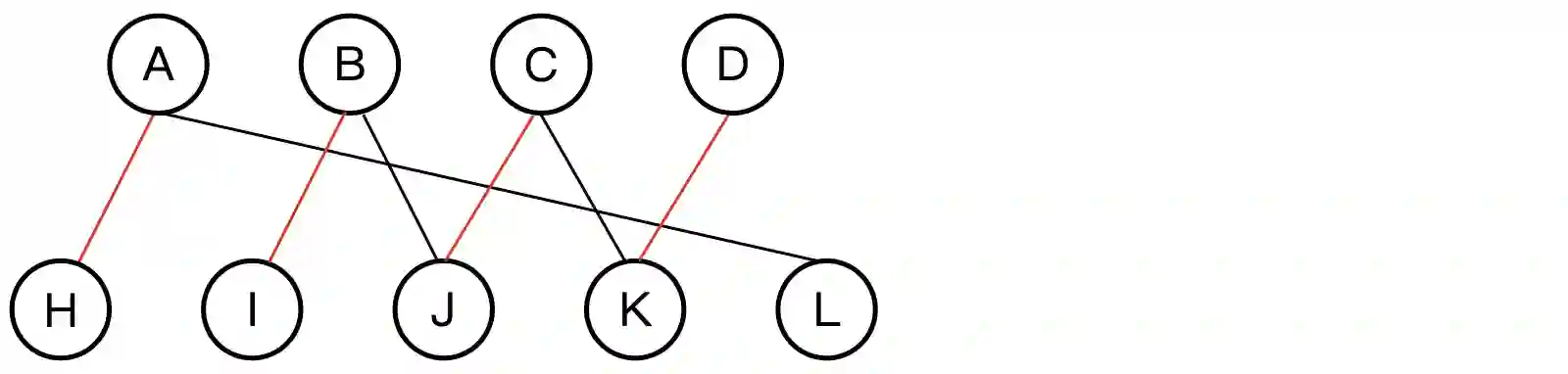
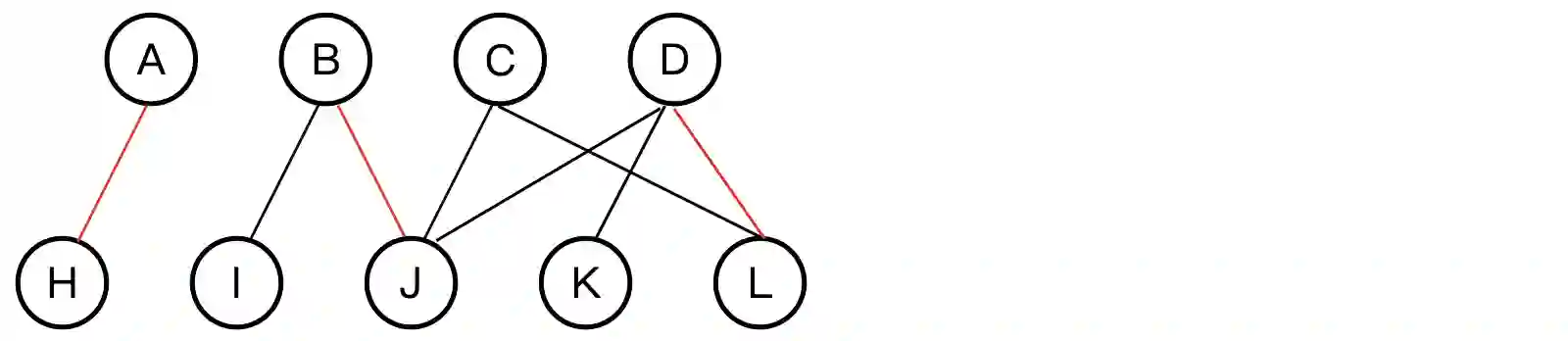
Given a weighted bipartite graph $G = (L, R, E, w)$, the maximum weight matching (MWM) problem seeks to find a matching $M \subseteq E$ that maximizes the total weight $\sum_{e \in M} w(e)$. This paper presents a novel algorithm with a time complexity of $O(\min(X^3 + E, XE + X^2\log X))$, where $X = \min(|L|, |R|)$. Unlike many existing algorithms, our approach supports real-valued weights without additional constraints. Under this condition, our result improves upon the previous best-known bound of $O(VE + V^2\log V)$, or more specifically $O(XE + XV\log V)$, where $V = L \cup R$. The simplified suggested implementation is publicly available at \url{https://github.com/ShawxingKwok/Kwok-algorithm}, with the average-case time complexity of $\tilde{O}(E + LR)$ roughly evaluated from theory and experimental results on random graphs.