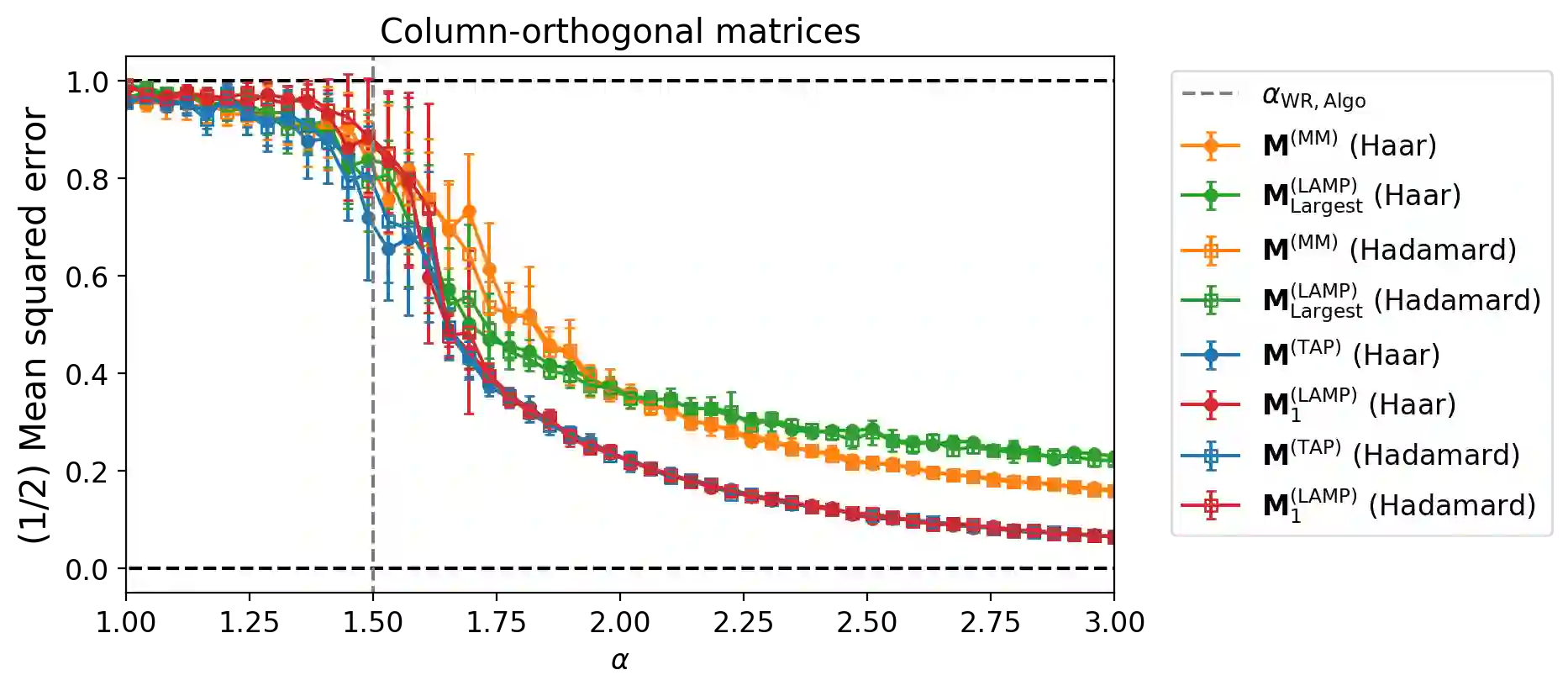
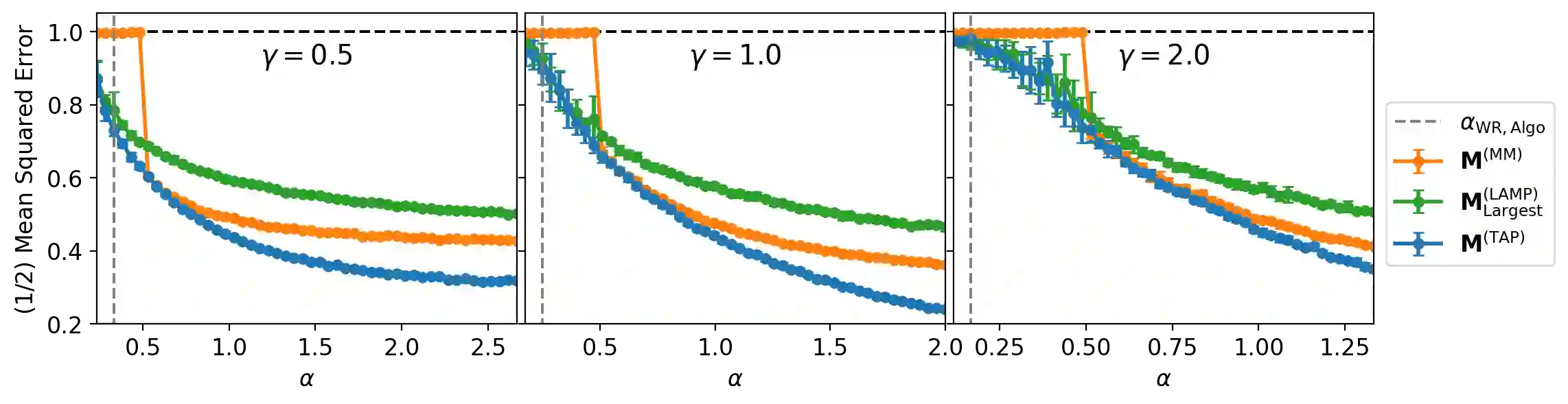
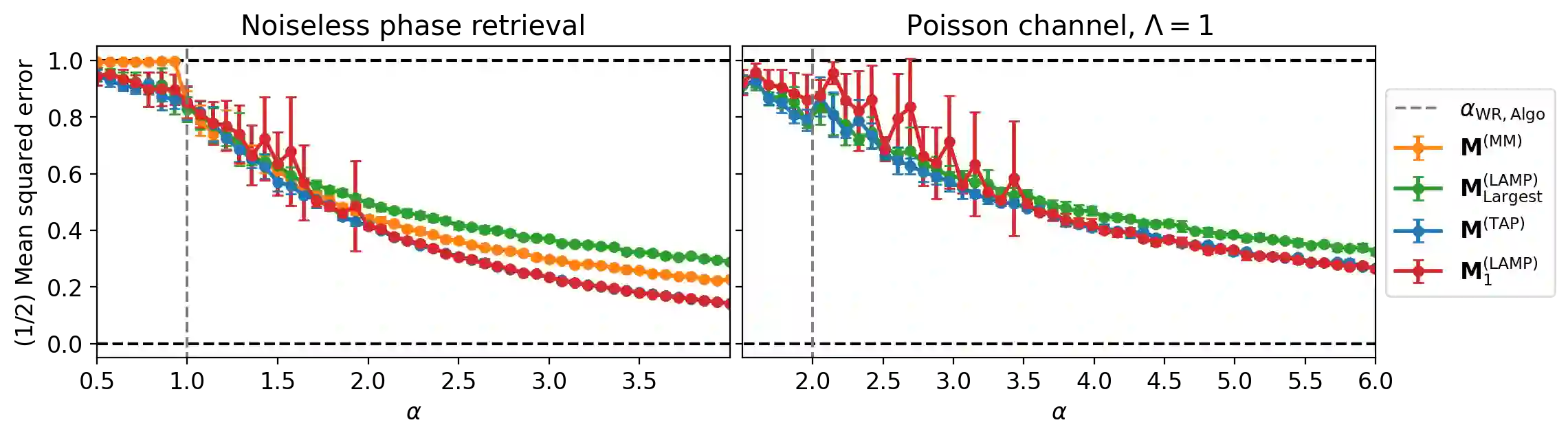
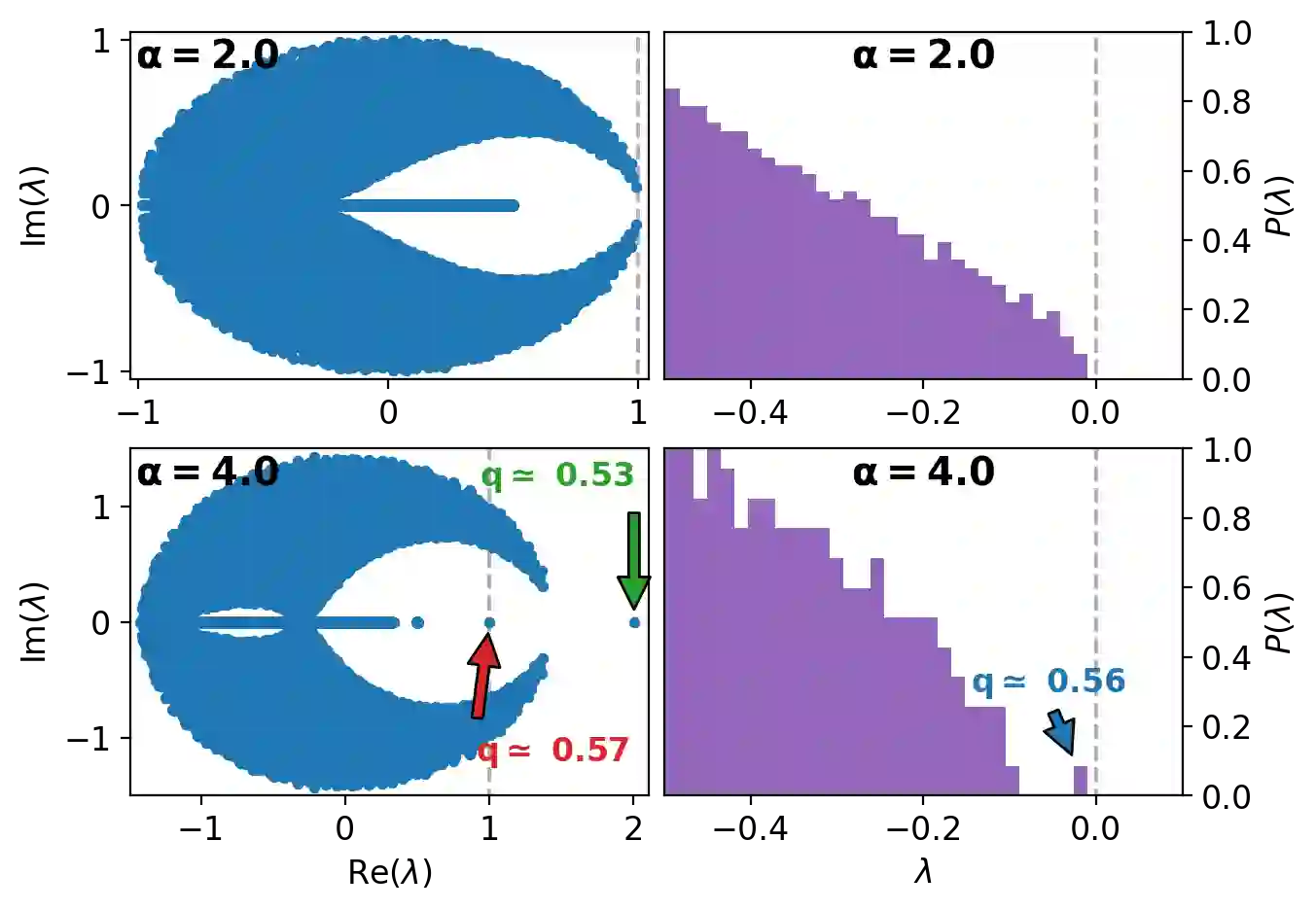
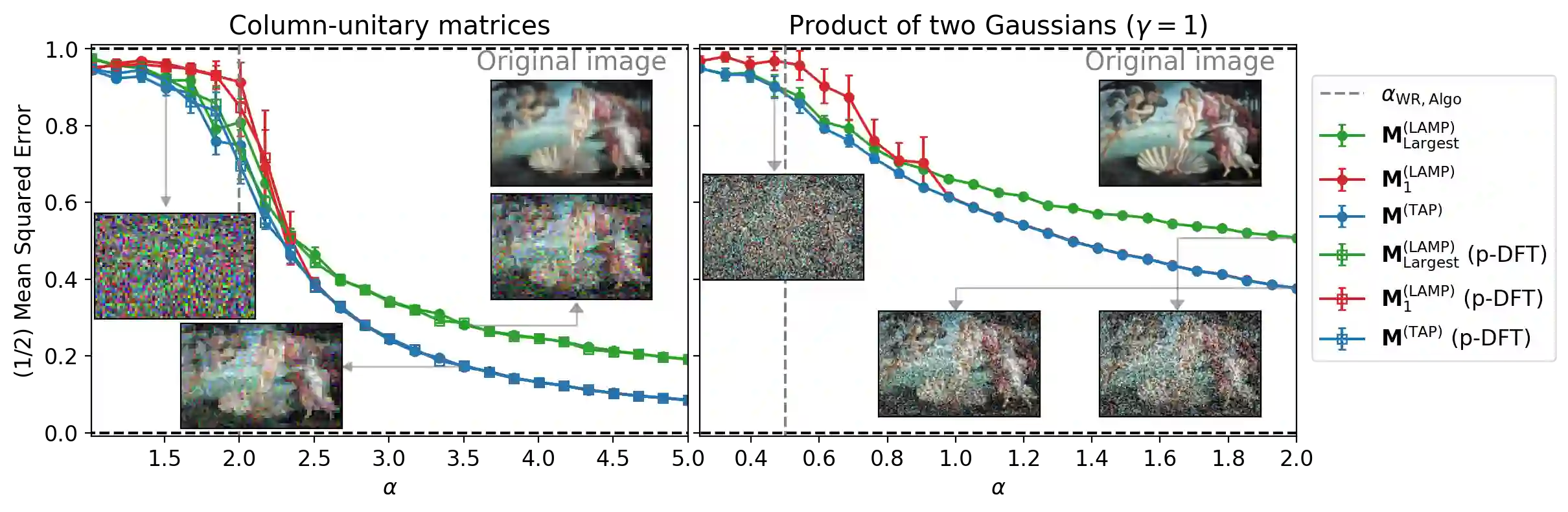
We consider the phase retrieval problem, in which the observer wishes to recover a $n$-dimensional real or complex signal $\mathbf{X}^\star$ from the (possibly noisy) observation of $|\mathbf{\Phi} \mathbf{X}^\star|$, in which $\mathbf{\Phi}$ is a matrix of size $m \times n$. We consider a \emph{high-dimensional} setting where $n,m \to \infty$ with $m/n = \mathcal{O}(1)$, and a large class of (possibly correlated) random matrices $\mathbf{\Phi}$ and observation channels. Spectral methods are a powerful tool to obtain approximate observations of the signal $\mathbf{X}^\star$ which can be then used as initialization for a subsequent algorithm, at a low computational cost. In this paper, we extend and unify previous results and approaches on spectral methods for the phase retrieval problem. More precisely, we combine the linearization of message-passing algorithms and the analysis of the \emph{Bethe Hessian}, a classical tool of statistical physics. Using this toolbox, we show how to derive optimal spectral methods for arbitrary channel noise and right-unitarily invariant matrix $\mathbf{\Phi}$, in an automated manner (i.e. with no optimization over any hyperparameter or preprocessing function).
翻译:我们考虑阶段检索问题, 观察者希望从 $ mathb_Phi}\ mathb{X{star} 的( 可能很吵的) 观察 $ mathbb_Phi} \ mathb{Xstar} 美元, 美元是一个大小的矩阵 $m\ f\ f\ phi} 美元。 我们考虑一个 maph{ high_ situ} 设置, 美元, 美元/ 美元= mathcal{O}(1)$ 美元, 以及一大批( 可能相关) 随机矩阵 $\ mathbf_Phi} 美元 和观察频道的( 可能具有关联性) 美元 。 光谱方法是一个强大的工具, 用来获得 $mathbxf{X} 美元信号的近似值观测, 然后可以用低计算成本作为后续算法的初始化。 在本文中, 我们扩展和统一先前的光谱方法, 以 美元= 平面检索问题 的平面 。 右 [ 我们使用直径分析 的直观 工具 的方式, 显示 一种直径分析 的方法, 一种直观 的方法 。